Аннуитет. Расчет периодического платежа в EXCEL. Срочный вклад

Рассчитаем в MS EXCEL сумму регулярного платежа в случае накопления определенной суммы. Сделаем это как с использованием функции ПЛТ() , так и впрямую по формуле аннуитетов. Также составим таблицу регулярных платежей с расшифровкой накопленной суммы и начисленных процентов.

Аннуитетная схема предусматривает пополнение вклада периодическими равновеликими платежами (например, ежемесячными). Такой равновеликий платеж называется аннуитет. В аннуитетной схеме предполагается неизменность процентной ставки по кредиту в течение всего периода накопления. Начисление процентов (капитализация), также происходит регулярно: период начисления процентов равен периоду внесения взносов.

Задача1

Требуется накопить за 5 лет сумму 1 000 000 руб. Начальная сумма вклада =0. Определить величину регулярных пополнений вклада, если процентная ставка составляет 10% годовых, пополнение вклада производится ежеквартально, капитализация процентов также производится ежеквартально. См. файл примера .

Расчет суммы регулярного пополнения вклада, произведем сначала с помощью финансовой функции MS EXCEL ПЛТ() .

Эта функция имеет такой синтаксис: ПЛТ(ставка; кпер; пс; [бс]; [тип]) PMT(rate, nper, pv, [fv], [type]) – английский вариант.

Примечание . Функция ПЛТ() входит в надстройку «Пакет анализа». Если данная функция недоступна или возвращает ошибку #ИМЯ?, то включите или установите и загрузите эту надстройку (в MS EXCEL 2007/2010 надстройка «Пакет анализа» включена по умолчанию).

Примечание . Обзор всех функций аннуитета найдете здесь .

Первый аргумент – Ставка. Это процентная ставка именно за период, т.е. в нашем случае за квартал, т.е. 10%/4 (в году 4 квартала). Кпер – общее число периодов платежей по аннуитету, т.е. 20 (4 кв. в году*5 лет) Пс - Приведенная стоимость , т.е. стоимость приведенная к текущему моменту. В нашем случае, это начальная сумма на расчетном счету, т.е. 0. Бс - Будущая стоимость вклада в конце срока (по истечении числа периодов Кпер). Бс - требуемое значение остатка средств после последнего взноса. В нашем случае Бс = 1 000 000. Тип - число 0 или 1, обозначающее, когда должно производиться начисление %. 0 – в конце периода, 1 – в начале. Если этот параметр опущен, то он считается =0 (наш случай).

Примечание . Если проценты начисляются в конце периода (каждого квартала), то тогда же производится пополнение вклада (т.к. указан аргумент ТИП=0 или опущен). Т.е., в последний день первого квартала мы пополнили счет на величину регулярного взноса, процент по вкладу за первый квартал =0. Если проценты начисляются в начале периода (каждого квартала), то тогда же производится пополнение вклада (аргумент ТИП=1). Т.е., в первый день первого квартала мы пополнили счет на величину регулярного взноса, но так как процент по вкладу начисляется также в первый день, то за первый квартал будет начислено 0.

Решение1 Итак, ежеквартальный платеж может быть вычислен по формуле =ПЛТ(10%/4; 5*4; 0;1000000; 0), т.е. -39147,13р. Знак минус показывает, что мы имеем разнонаправленные денежные потоки: накапливаем деньги (тем самым отнимаем их из нашего бюджета), и получаем от банка +1000000, когда забираем деньги в конце срока. Альтернативная формула для расчета платежа: =(Пс*ставка*(1+ ставка)^ Кпер /((1+ ставка)^ Кпер -1)+ ставка /((1+ ставка)^ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка +1);1)

Если период начисления процентов и регулярных взносов не совпадает

Если проценты начисляются, например, ежегодно, а взносы делаются ежемесячно, то такой денежный поток не является аннуитетом. Следовательно, функцию ПЛТ() и другие функции для расчета параметров аннуитета применять нельзя.

Таблица пополнения вклада

Составим таблицу пополнения вклада.

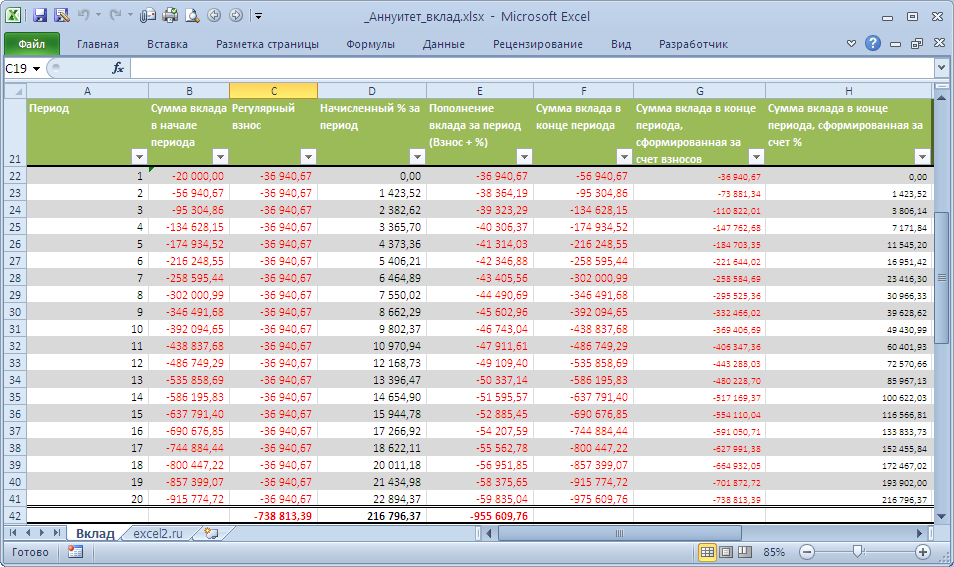
Вклад пополняется из 2-х источников: первый – это регулярные взносы, второй – начисленные за период проценты (на накопленную к данному моменту сумму вклада). Для вычисления регулярно начисляемых процентов используется функция ПРПЛТ (ставка; период; кпер; пс; [бс]; [тип])

Таким образом, вклад регулярно пополняется на величину =-ПЛТ(10%/4; 20; 0;1000000; 0) + ПРПЛТ(10%/4; период; 20; 0; 1000000; 0) , где период – это номер периода, в который требуется подсчитать величину пополнения. Тот же самый результат дает формула =-ОСПЛТ(10%/4; период; 20; 0; 1000000; 0)

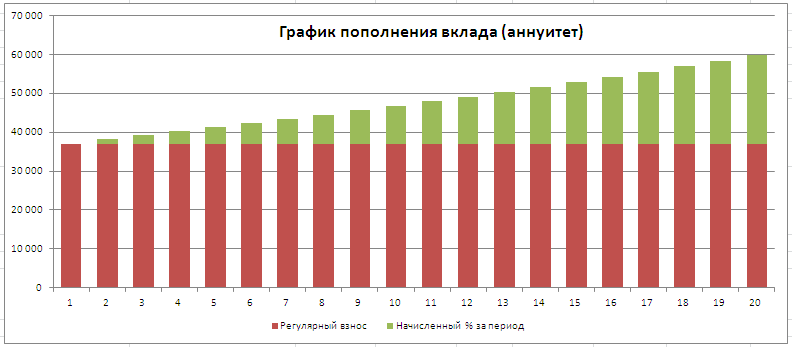
Соотношение величины взноса и начисленных процентов хорошо демонстрирует график, приведенный в файле примера .

Примечание . В статье Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа) показано как рассчитать величину регулярной суммы для погашения кредита или ссуды в случае применения аннуитетной схемы.

Задача2

Требуется накопить за 5 лет сумму 1 000 000 руб. Определить величину регулярных пополнений вклада, если процентная ставка составляет 10% годовых, пополнение вклада производится ежеквартально, капитализация процентов также производится ежеквартально, на счету уже содержится 100 000 руб.

Решение2 Накопить за счет взносов нам потребуется всего 900 000руб. (1 000 000-100 000). Ежеквартальный платеж может быть вычислен по формуле =ПЛТ(10%/4; 5*4; -100000;1000000; 0) , результат -32732,42р.

Все параметры функции ПЛТ() выбираются аналогично предыдущей задаче, кроме значения ПС = -100000р., который требует пояснения. Вспомним, что для аннуитета справедливо тождество: ПС+СУММ(ОСПЛТ())+БС=0, т.е. ПС+(-900000р.)+1 000 000=0. Отсюда получим ПС = -100000р.

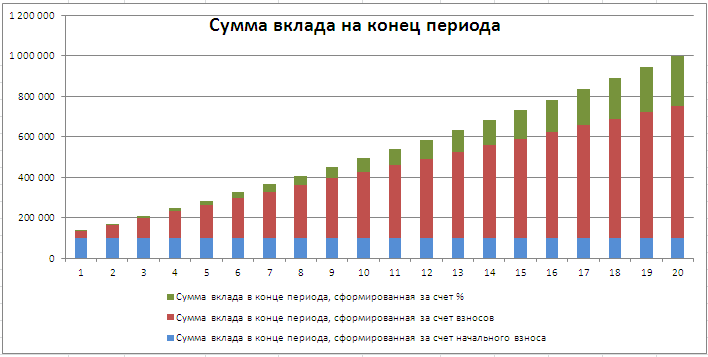
Примечание . В файле примера также приведен расчет графика прироста вклада без использования формул аннуитета (см. столбцы K:O).