Дифференцированные платежи по кредиту в EXCEL

Составим в MS EXCEL график погашения кредита дифференцированными платежами.

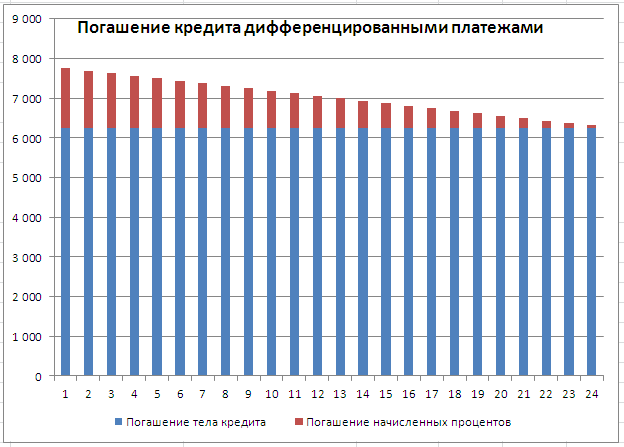
При расчете графика погашения кредита дифференцированными платежами сумма основного долга делится на равные части пропорционально сроку кредитования. Регулярно, в течение всего срока погашения кредита, заемщик выплачивает банку эти части основного долга плюс начисленные на его остаток проценты. Если кредитным договором период погашения установлен равным месяцу, то из месяца в месяц сумма основного долга пропорционально уменьшается. Поэтому при дифференцированных платежах основные расходы заемщик несет в начале кредитования, размеры ежемесячных платежей в этот период самые большие. Но постепенно, с уменьшением остатка ссудной задолженности, уменьшается и сумма начисленных процентов по кредиту. Выплаты по кредиту значительно сокращаются и становятся не такими обременительными для заемщика.

Примечание . При расчете кредита дифференцированными платежами сумма переплаты по процентам будет ниже, чем при аннуитетных платежах . Не удивительно, что сегодня практически все российские банки применяют в расчетах аннуитетную схему погашения кредита. Сравнение двух графиков погашения кредита приведено в статье Сравнение графиков погашения кредита дифференцированными аннуитетными платежами в MS EXCEL .

График погашения кредита дифференцированными платежами

Задача . Сумма кредита =150т.р. Срок кредита =2 года, Ставка по кредиту = 12%. Погашение кредита ежемесячное, в конце каждого периода (месяца).

Решение. Сначала вычислим часть (долю) основной суммы кредита, которую заемщик выплачивает за период: =150т.р./2/12, т.е. 6250р. (сумму кредита мы разделили на общее количество периодов выплат =2года*12 (мес. в году)). Каждый период заемщик выплачивает банку эту часть основного долга плюс начисленные на его остаток проценты. Расчет начисленных процентов на остаток долга приведен в таблице ниже – это и есть график платежей.

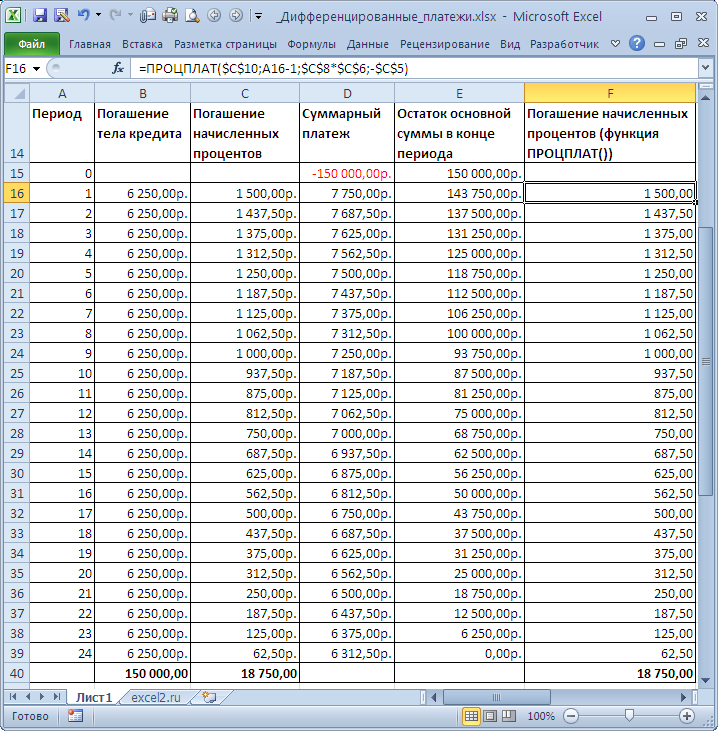
Для расчета начисленных процентов может быть использована функция ПРОЦПЛАТ(ставка;период;кпер;пс), где Ставка - процентная ставка за период ; Период – номер периода, для которого требуется найти величину начисленных процентов; Кпер - общее число периодов начислений; ПС – приведенная стоимость на текущий момент (для кредита ПС - это сумма кредита, для вклада ПС – начальная сумма вклада).

Примечание . Не смотря на то, что названия аргументов совпадают с названиями аргументов функций аннуитета – ПРОЦПЛАТ() не входит в группу этих функций (не может быть использована для расчета параметров аннуитета).

Примечание . Английский вариант функции - ISPMT(rate, per, nper, pv)

Функция ПРОЦПЛАТ() предполагает начисление процентов в начале каждого периода (хотя в справке MS EXCEL это не сказано). Но, функцию можно использовать для расчета процентов, начисляемых и в конце периода для это нужно записать ее в виде ПРОЦПЛАТ(ставка;период-1;кпер;пс), т.е. «сдвинуть» вычисления на 1 период раньше (см. файл примера ). Функция ПРОЦПЛАТ() начисленные проценты за пользование кредитом указывает с противоположным знаком, чтобы отличить денежные потоки (если выдача кредита – положительный денежный поток («в карман» заемщика), то регулярные выплаты – отрицательный поток «из кармана»).

Расчет суммарных процентов, уплаченных с даты выдачи кредита

Выведем формулу для нахождения суммы процентов, начисленных за определенное количество периодов с даты начала действия кредитного договора. Запишем суммы процентов начисленных в первых периодов (начисление и выплата в конце периода): ПС*ставка (ПС-ПС/кпер)*ставка (ПС-2*ПС/кпер)*ставка (ПС-3*ПС/кпер)*ставка … Просуммируем полученные выражения и, используя формулу суммы арифметической прогрессии, получим результат. =ПС*Ставка* период*(1 - (период-1)/2/кпер) Где, Ставка – это процентная ставка за период (=годовая ставка / число выплат в году), период – период, до которого требуется найти сумму процентов. Например, сумма процентов, выплаченных за первые полгода пользования кредитом (см. условия задачи выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р. За весь срок будет выплачено =ПС*Ставка*(кпер+1)/2=18750р. Через функцию ПРОЦПЛАТ() формула будет сложнее: =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ("1:"&кпер))-1;кпер;-ПС))