Вращение фигур в трехмерном пространстве (3D Rotation) в EXCEL
21 июля 2017 г.
- Группы статей
- Матрицы
- Диаграммы и графики
Научимся вращать в MS EXCEL трехмерные фигуры вокруг координатных осей Х, Y, Z, а также поворачивать плоскости вокруг произвольно заданной оси. Для этого используем соответствующие матрицы вращения. Также покажем, что проекция фигуры на плоскость, построенная с помощью диаграммы типа Точечная, может служить альтернативой диаграмме типа Поверхность.
Вращать объемные фигуры в MS EXCEL можно и встроенными средствами (см. статью Трехмерные диаграммы (поверхности и изолинии) в MS EXCEL ). Однако, в этом случае фигура изображена в виде поверхности, что не всегда удобно.
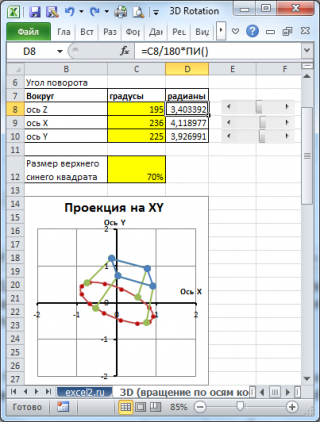
Здесь фигуру будем представлять в виде точек (вершин) и ребер, их соединяющих. В качестве примера возьмем фигуру в виде цирковой тумбы (широкое круглое основание красного цвета и квадратное место для сидения синего цвета).
В файле примера можно найти вышеуказанную диаграмму. В данной диаграмме использовано 3 ряда данных (для каждого цвета), а масштаб осей фиксирован, чтобы не исказить пропорции.
СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL .
Для вращения объемных фигуры будем использовать матрицы , поэтому тем, кто не знаком с этим подходом рекомендуем прочитать статью Трансформация фигур в двухмерном пространстве (2D Transformation) в MS EXCEL .
Построение "объемной" фигуры
Круглое основание фигуры красного цвета разместим в плоскости Z=0, т.е. z-координаты у всех точек основания равны 0. Координаты x и y зададим с помощью угла в радианах от 0 до 2*ПИ. Это можно сделать с помощью функций SIN() и COS() . Сделаем 14 точек, причем первая и последняя точки должны совпадать, чтобы линии, соединяющие эти точки, замкнулись .
Аналогично создадим синий квадрат из 4-х точек. Z-координаты квадрата положим равными 1. Наконец, соединим вершины квадрата с основанием линиями зеленого цвета.
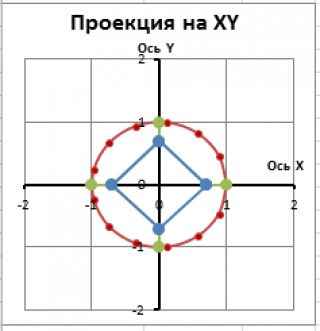
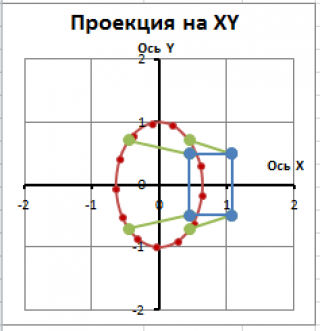
Вид сверху (вдоль оси Z на плоскость XY) должен быть таким.
Вращение вокруг координатных осей
Сначала повернем нашу фигуру вокруг оси Z на 45 градусов. Матрица поворота (Rotation matrix) будет такой же, как и в двухмерном случае, только необходимо добавить еще одну строку и столбец как у единичной матрицы.
Для ввода угла поворота можно настроить элемент управления Счетчик (см. файл примера ).
Координаты фигуры после поворота получаются путем умножения матрицы на известные координаты. В EXCEL это можно реализовать с помощью формулы:
=ТРАНСП(МУМНОЖ($H$14:$J$16;ТРАНСП(B31:D31)))
Для ввода формулы выделите 3 ячейки в строке (куда нужно поместить новые координаты), установите курсор в Строку формул , введите формулу, затем нажмите CTRL+SHIFT+ENTER.
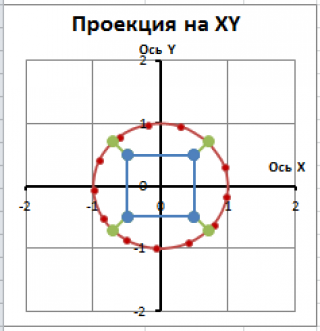
В итоге получим вот такую картинку:
Для вращения вокруг других координатных осей используются соответствующие матрицы поворота:
Вращая фигуру в трех плоскостях можно лучше представить как она выглядит в объеме.
Поворот плоскости вокруг произвольной оси
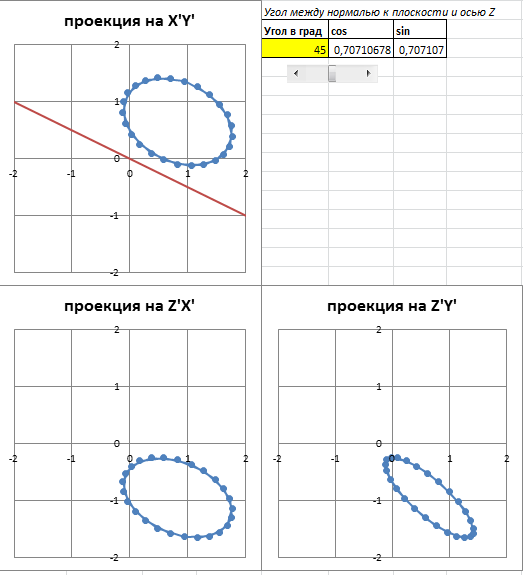
Пусть окружность расположена в плоскости Z=0. Также дана прямая, которая также лежит в плоскости Z=0 и проходит через центр координат (0;0;0).
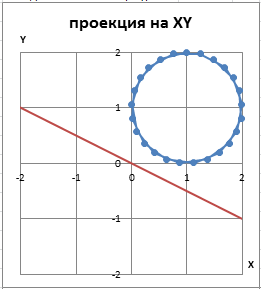
Проекции на другие координатные плоскости выглядят так:
Повернем плоскость, на которой находится наша окружность, вдоль прямой на угол Θ к оси Z (например, 45 градусов).
Вращение можно осуществить с помощью вот такой матрицы поворота:
u x , u y и u z - координаты единичного вектора, представляющего ось вращения. В нашем случае вектор оси равен (-2;1;0). Кординаты этого вектора нужно разделить на его модуль , чтобы получить единичный вектор.
Для построения матрицы поворота используем Имена : ячейкам, содержащие координаты вектора и cos и sin угла поворота, присвоим имена как в матрице поворота.
Координаты окружности после поворота получаются путем умножения матрицы на известные координаты. В EXCEL это можно реализовать с помощью формулы:
=ТРАНСП(МУМНОЖ($C$11:$E$13;ТРАНСП(B52:D52)))
Для ввода формулы выделите 3 ячейки в строке (куда нужно поместить новые координаты), установите курсор в Строку формул , введите формулу, затем нажмите CTRL+SHIFT+ENTER.
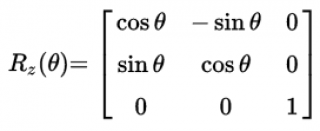
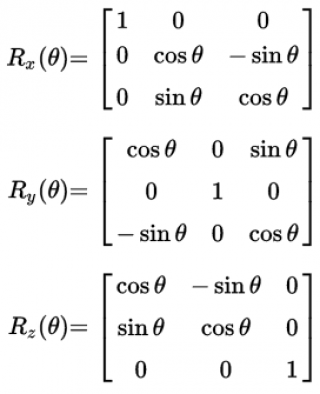
Комментарии