Трансформация фигур в двухмерном пространстве (2D Transformation) в EXCEL

Трансформация (преобразование) геометрической фигуры означает ее изменение по определенным правилам. Например, вращение, смещение или изменение масштаба некого прямоугольника на плоскости. Правила, по которым происходит изменение, будем записывать в матричном виде. Используем произведение матриц для применения к фигуре сразу нескольких преобразований. Также используем однородную систему координат (Homogenous Coordinates). Здесь рассмотрим трансформацию в двумерном пространстве с использованием MS EXCEL.

Пусть имеется исходная фигура (трапеция). Нам известны координаты ее вершин, геометрическая фигура построена с помощью диаграммы типа Точечная .

СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL .

Примечание : В MS EXCEL есть объект Фигура (Вкладка Вставка, группа Иллюстрации, кнопка Фигуры). Так вот, рассматриваемые здесь геометрические фигуры не имеют никакого отношения к этим объектам.

Выделим произвольную вершину трапеции красным цветом и назовем ее опорной точкой. Ее координаты (1;1). Опорную точку будем иногда помещать в центр координат, чтобы упростить преобразования.

Смещение фигуры (Translation)

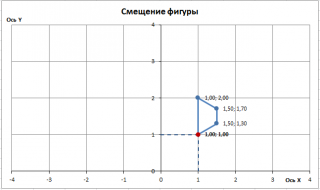
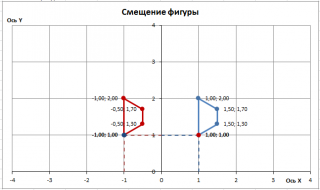
Для начала, сместим фигуру в заданную точку, задав координаты новой опорной точки:  пусть это будет точка (-1;1).

Чтобы получить остальные координаты фигуры после смещения, вычислим координаты вектора смещения (translation vector or shift vector), вычтя из новых координат исходные координаты опорной точки (см. файл примера ).

Теперь, прибавив к исходным координатам координаты вектора смещения получим новые координаты фигуры.

Вместо вектора смещения для нахождения новых координат фигуры можно использовать матричный подход . Правда, именно для смещения фигуры нам для этого придется ввести понятие однородных координат (Homogenous Coordinates). Не вдаваясь в теорию, преобразование к однородным координатам сводится к добавлению для каждой точки фигуры еще одной вспомогательной координаты равной 1. Например, координаты опорной точки будут выглядеть в однородной системе координат как (1;1;1).

В нашем двумерном случае матрица смещения будет 3x3.

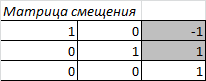
В серых ячейках содержатся новые координаты опорной точки, остальные элементы матрицы являются элементами единичной матрицы.

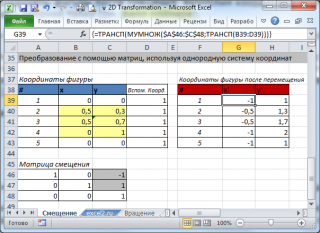
Перемножив матрицу смещения на координаты исходных точек (в виде столбца), получим новые координаты (в виде столбца). Далее транспонируем столбец в строку и получим новые координаты точек фигуры после смещения. Все это можно сделать с помощью формулы массива :

=ТРАНСП(МУМНОЖ($A$46:$C$48;ТРАНСП(B39:D39)))

Вращение фигуры (Rotation)

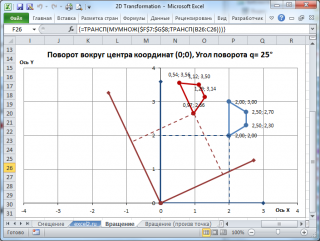
Сначала научимся вращать фигуру относительно центра координат. Угол поворота зададим в градусах, затем переведем в радианы. Повороту против часовой стрелки будет соответствовать положительный угол θ.

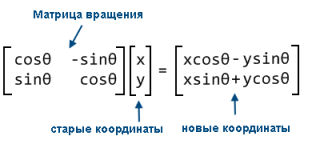
Для вычисления координат вершин фигуры после поворота мы будем использовать матрицу поворота 2х2 (rotation matrix).

Новые координаты получаются путем умножения матрицы на известные координаты. В EXCEL это можно реализовать с помощью формулы:

=ТРАНСП(МУМНОЖ($F$7:$G$8;ТРАНСП(B26:C26)))

Для ввода формулы выделите 2 ячейки в строке (куда нужно поместить новые координаты), установите курсор в Строку формул , введите формулу, затем нажмите CTRL+SHIFT+ENTER.

Для ввода угла поворота можно настроить элемент управления Счетчик (см. файл примера , лист Вращение).

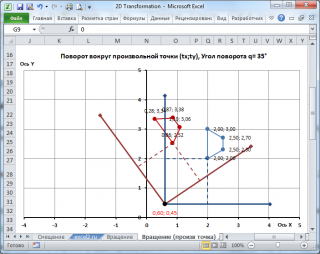
Если вращение нужно осуществить относительно произвольной точки, то нам снова потребуется однородная система координат (см. файл примера , лист Вращение (произв точка)).

В данном случае вращение можно представить как последовательность преобразований: смещение точки, вокруг которой будет производиться вращение в центр координат, собственно вращение, затем обратное смещение точки. Таким образом, мы имеем 3 матрицы.

Эти матрицы можно предварительно перемножить и использовать уже одну итоговую матрицу. В файле примера реализовано оба варианта.

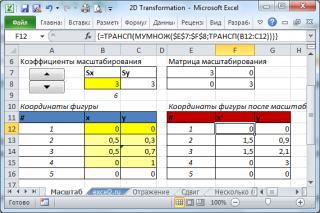
Масштабирование фигуры (Scaling)

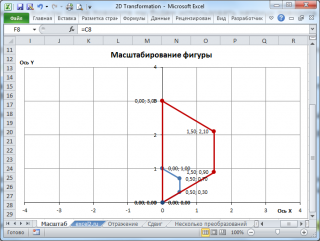
Еще одним типом преобразования является изменение масштаба. Поместим опорную точку фигуры в центр координат.

Матрица изменения масштаба представляет собой диагональную матрицу 2x2, все элементы которой равны. Если элементы больше 1, то фигура увеличивается, если меньше, то уменьшается.

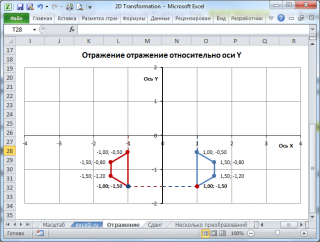
Отражение (Reflection)

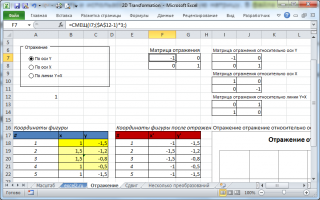
Фигуру можно отразить относительно осей координат или произвольной линии.

В файле примера настроена специальная форма на основе элемента управления Переключатель .

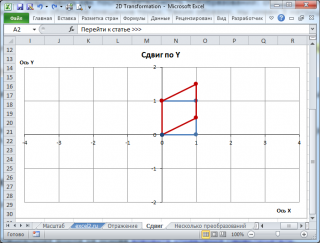
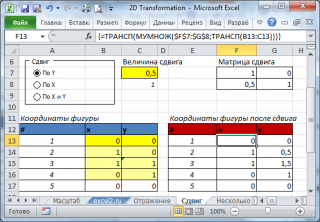
Сдвиг (Shear)

Наконец, последним преобразованием является Сдвиг. Например, при сдвиге по оси Y, точки фигуры смещаются по оси Y пропорционально значению координаты Х (линейное преобразование при котором параллельные прямые остаются параллельными).

Т.к. Х координаты левой стороны квадрата равны 0, то ее смещения не происходит, а сдвигается только правая.

Матрица сдвига выглядит так:

Серия преобразований

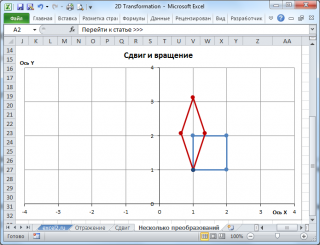
Преобразуем квадрат в ромб и повернем его.

Для этого нам потребуется сделать Сдвиг, а затем Вращение (последовательность имеет значение!). Если мы сначала повернем квадрат, а потом сдвинем его, то мы получим другую фигуру (произведение матриц в общем случае не коммутативно ).

Нам потребуется 4 матрицы: 2 матрицы для смещения фигуры в центр координат и обратно; матрица для Сдвига и матрица для Вращения.

Результирующую матрицу можно получить с помощью одной формулы массива :

=МУМНОЖ(МУМНОЖ(МУМНОЖ(J7:L9;N7:P9);R7:T9);V7:X9)