Вычисление длины (модуля) вектора в EXCEL

Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).

Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.

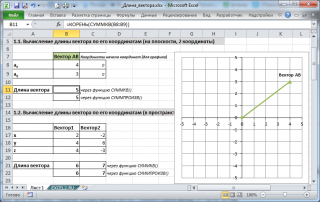
1. Вычисление длины вектора по его координатам

Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a _x и a _y , то длину вектора можно найти по формуле

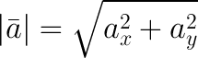
В случае вектора в пространстве добавляется третья координата

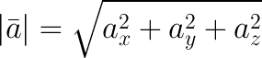
В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).

Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле = B8*B8+B9*B9 .

В файле примера также вычислена длина вектора в пространстве.

Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .

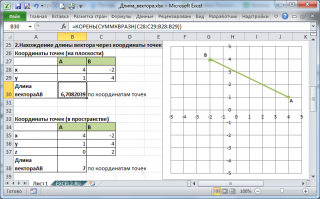
2. Нахождение длины вектора через координаты точек

Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))

В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.

Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.

По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.

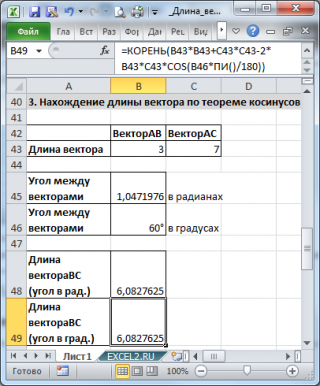
3. Нахождение длины вектора по теореме косинусов

Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).

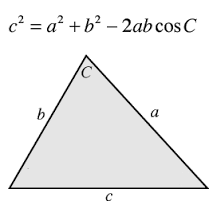
Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))

В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 - угол между ними в радианах (в долях числа ПИ() ).

Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))

Примечание : для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат , см. например, статью Отображение широты и долготы в MS EXCEL

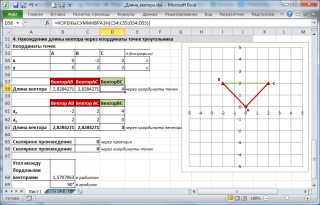
4. Нахождение длины вектора через координаты точек треугольника

Пусть заданы 3 точки треугольника, образованного векторами.

Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)) .

Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).

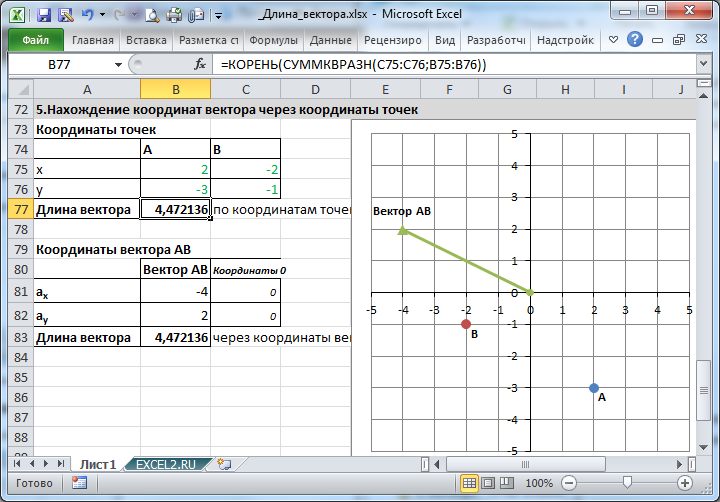
5. Нахождение координат вектора через координаты точек

Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.