Распределение Стьюдента (t-распределение). Распределения математической статистики в EXCEL
10 ноября 2016 г.
- Группы статей
- Распределения вероятностей
Рассмотрим Распределение Стьюдента (t-распределение). С помощью функции MS EXCEL СТЬЮДЕНТ.РАСП() построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.
Распределение Стьюдента (также называется t -распределением ) применяется в различных методах математической статистики:
- при построении доверительных интервалов для среднего (используется функция ДОВЕРИТ.СТЬЮДЕНТ() );
- для оценки различия двух выборочных средних (используется функция СТЬЮДЕНТ.ТЕСТ() );
- при проверке гипотез (выборка небольшого размера, стандартное отклонение не известно) ,
- в линейном регрессионном анализе (при проверке гипотез на значимость отдельных регрессионных коэффициентов).
Определение : Если случайная величина Z распределена по стандартному нормальному закону N(0;1) и случайная величина U имеет распределение ХИ-квадрат с ν степенями свободы, то случайная величина T=Z/√(U/v) имеет t-распределение .
Плотность распределения Стьюдента выражается формулой:
при −∞ < t < ∞
СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Распределение Стьюдента (англ. Student ’ s t - distribution ) зависит от одного параметра, который называется степенью свободы ( df , degrees of freedom ). Например, при построении доверительного интервала для среднего число степеней свободы равно df=n-1, где n – размер выборки . При увеличении числа степеней свободы это распределение стремится к стандартному нормальному распределению . В центральной части распределения (около 0) при df=25, относительная разница со стандартным нормальным распределением составляет порядка 1%, а при df=100 разница составляет 0,25%.
По аналогии со стандартным нормальным распределением , t -распределение часто называется «стандартизированным», т.к. у него нет параметра отвечающего за положение ( среднее всегда равно 0).
Дисперсию t -распределения можно вычислить по формуле =df/(df-2)
Графики функций
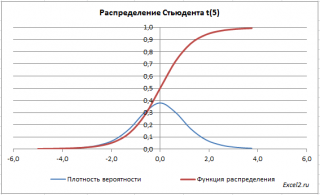
В файле примера на листе График приведены графики плотности распределения вероятности и интегральной функции распределения .
График плотности распределения Стьюдента , как и стандартного нормального распределения , является симметричным и колоколообразным, но с более тяжелыми хвостами.
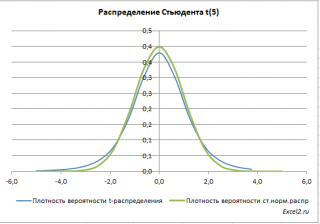
Ниже для сравнения приведены графики плотности стандартного нормального распределения и распределения Стьюдента.
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
t-распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для t-распределения имеется функция СТЬЮДЕНТ.РАСП() , английское название - T.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина Х, имеющая распределение Стьюдента , примет значение меньше или равное х, P(X <= x)).
Примечание : В файле примера на листе Функции приведены основные функции MS EXCEL, связанные с этим распределением.
Кроме этой функции в MS EXCEL имеется еще довольно много других функций, относящихся к данному распределению, но по большому счету их функционал покрывается функцией СТЬЮДЕНТ.РАСП() .
Кроме того, СТЬЮДЕНТ.РАСП() является единственной функцией, которая возвращает плотность вероятности (третий аргумент должен быть равным ЛОЖЬ). Остальные функции возвращают интегральную функцию распределения , т.е. вероятность того, что случайная величина примет значение из указанного диапазона: P(X <= x), P(X > x) или даже P(|X| > x).
Очевидно, что справедливо равенство
=СТЬЮДЕНТ.РАСП.ПХ(x;n)+СТЬЮДЕНТ.РАСП(x;n;ИСТИНА)=1 т.к. первое слагаемое вычисляет вероятность P(X > x), а второе P(X <= x).
До MS EXCEL 2010 в EXCEL была только функция СТЬЮДРАСП() , которая позволяет вычислить функцию распределения (точнее - правостороннюю вероятность, т.е. P(X>x)) и объединяет возможности нескольких новых функций MS EXCEL 2010: СТЬЮДЕНТ.РАСП(x; n; ЛОЖЬ) , СТЬЮДЕНТ.РАСП.ПХ() , СТЬЮДЕНТ.РАСП.2Х() . Функция СТЬЮДРАСП() оставлена в MS EXCEL 2010 для совместимости.
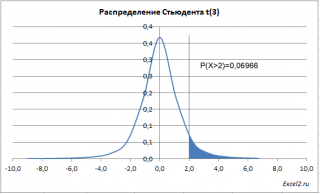
- Если значение аргумента «хвосты» = 1, функция СТЬЮДРАСП() вычисляет правостороннюю вероятность P(X > x), где X — случайная переменная, соответствующая t-распределению. Под термином «хвост» подразумевается «хвост» распределения, в данном случае правый. На графике плотности вероятности этому «хвосту» будет соответствовать площадь фигуры под графиком (выделена синим), которая ограничена слева вертикальной линией X = x.
- Если значение аргумента "хвосты" = 2, функция СТЬЮДРАСП() вычисляет вероятность P(|X| > x) или другими словами P(X > x или X < -x). Т.е. формула =СТЬЮДРАСП(x;n;2) эквивалентна =СТЬЮДРАСП(x;n;1)*2
- Функцией СТЬЮДРАСП() значения x < 0 не поддерживаются и нельзя записать СТЬЮДРАСП(-x;n;1) . Чтобы вычислить вероятность P(X <= x), в том числе и для отрицательных х, используйте формулу =ЕСЛИ(x>0;СТЬЮДРАСП(x;n;1);1-СТЬЮДРАСП(-x;n;1)) .
Примеры
Найдем вероятность, что случайная величина Х примет значение меньше или равное заданного x : P(X <= x ). Это можно сделать несколькими функциями:
- =СТЬЮДЕНТ.РАСП(x; n; ИСТИНА) или =1-СТЬЮДЕНТ.РАСП(-x; n; ИСТИНА) , используется свойство симметричности плотности распределения относительно оси Х.
- =1-СТЬЮДЕНТ.РАСП.ПХ(x;n) или =СТЬЮДЕНТ.РАСП.ПХ(-x;n) , функция СТЬЮДЕНТ.РАСП.ПХ() возвращает вероятность P(X > x), так называемую правостороннюю вероятность, поэтому, чтобы найти P(X <= x), необходимо вычесть ее результат от 1 или воспользоваться свойством t-распределения t(-х)=1-t(x).
- =1-СТЬЮДЕНТ.РАСП.2Х(x;n)/2 или =1-СТЬЮДРАСП(x;n;2)/2 , в этой формуле х может принимать только положительные значения (подробнее об этой функции см. ниже);
- =1-СТЬЮДРАСП(x; n; 1) , в этой формуле х может принимать только положительные значения, функция СТЬЮДРАСП() , как и СТЬЮДЕНТ.РАСП.ПХ() , возвращает «правостороннюю вероятность», т.е. P(X > x).
Аналогичные вычисления для P(X > x) и P(|X| > x) приведены в файле примера на листе Функции , в том числе и для x<0.
Обратная функция t-распределения
Обратная функция используется для вычисления альфа - квантилей , т.е. для вычисления значений x при заданной вероятности альфа , причем х должен удовлетворять выражению P{X<=x}= альфа .
Функция СТЬЮДЕНТ.ОБР() используется для вычисления как двухсторонних, так и односторонних доверительных интервалов . А функции СТЬЮДЕНТ.ОБР.2Х() и СТЬЮДРАСПОБР() созданы специально для вычисления квантилей , необходимых для расчета двусторонних доверительных интервалов: в качестве аргумента нужно указывать уровень значимости альфа , а не альфа/2 , как для СТЬЮДЕНТ.ОБР() .
Вышеуказанные функции можно взаимозаменять, т.к. нижеуказанные формулы возвращают одинаковый результат: =СТЬЮДЕНТ.ОБР(альфа;n) =-СТЬЮДРАСПОБР(альфа*2;n) =-СТЬЮДЕНТ.ОБР.2Х(альфа*2;n)
Некоторые примеры расчетов приведены в файле примера на листе Функции .
Примечание : Ниже приведено соответствие русских и английских названий функций: СТЬЮДЕНТ.РАСП.ПХ() - англ. название T.DIST.RT, т.е. T-DISTribution Right Tail, the right-tailed Student's t-distribution СТЬЮДЕНТ.РАСП.2Х() - англ. название T.DIST.2T, т.е. T-DISTribution 2 Tails СТЬЮДЕНТ.ОБР() - англ. название T.INV, т.е. T-distribution INVerse СТЬЮДРАСП() - англ. название TDIST, т.е. T-DISTribution СТЬЮДРАСПОБР() - англ. название TINV, т.е. T-distribution INVerse (the right-tailed inverse of the Student's t-distribution) СТЬЮДЕНТ.ОБР.2Х() - англ. название T.INV.2T
Функции MS EXCEL, использующие t-распределение
Как было сказано выше, при построении доверительных интервалов используется функция ДОВЕРИТ.СТЬЮДЕНТ() - англ. название CONFIDENCE.T.
Например, формула =ДОВЕРИТ.СТЬЮДЕНТ(альфа;СТАНДОТКЛОН.В(B20:B79); СЧЁТ(B20:B79)) эквивалентна классической формуле для вычисления доверительного интервала =СТЬЮДЕНТ.ОБР(1-альфа/2; СЧЁТ(B20:B79)-1)* СТАНДОТКЛОН.В(B20:B79)/КОРЕНЬ(СЧЁТ(B20:B79))
где предполагается, что выборка находится в диапазоне B20:B79 .
Как видим, особых преимуществ в использовании ДОВЕРИТ.СТЬЮДЕНТ() нет.
Другая функция - СТЬЮДЕНТ.ТЕСТ() - англ. название T.TEST, используется для оценки различия двух выборочных средних .
Оценка параметров распределения
Т.к. обычно t-распределение используется для целей математической статистики (вычисление доверительных интервалов, проверки гипотез и др.), и практически никогда для построения моделей реальных величин, то для этого распределения обсуждение оценки параметров распределения здесь не производится.
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
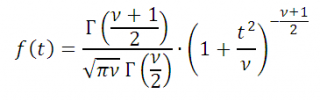
Комментарии