Проверка распределения на нормальность в EXCEL

Построение графика проверки распределения на нормальность ( Normal Probability Plot ) является графическим методом определения соответствия значений выборки нормальному распределению.

Предположим, что имеется некий набор данных. Требуется оценить, соответствует ли данная выборка нормальному распределению .

Рассмотренный ниже графический метод основан на субъективной визуальной оценке данных. Объективным же подходом является, например, анализ степени согласия гипотетического распределения с наблюдаемыми данными (goodness-of-fit test), который рассмотрен в статье Проверка простых гипотез критерием Пирсона ХИ-квадрат .

Из-за наличия неустранимой статистической ошибки выборки, присущей случайной величине, невозможно однозначно ответить на вопрос «Взята ли данная выборка из нормального распределения или нет». Поэтому, рассмотренный графический метод, скорее, дает ответ на вопрос «Разумно ли предположение, что оцениваемая выборка взята из нормального распределения »?

Рассмотрим алгоритм построения графика проверки распределения на нормальность ( Normal Probability Plot ) :

• Отсортируйте значения выборки по возрастанию (значения выборки x _j будут отложены по горизонтальной оси Х);
• Каждому значению x _j выборки поставьте в соответствие значения (j-0,5)/n, где n – количество значений в выборке , j – порядковый номер значения от 1 до n. Этот массив будет содержать значения от 0,5/n до (n-0,5)/n. Таким образом, диапазон от 0 до 1 будет разбит на равномерные отрезки. Этот диапазон соответствует вероятности наблюдения значений случайной величины Z<=z _j ;
• Преобразуем значения массива, полученные на предыдущем шаге, с помощью обратной функции стандартного нормального распределения НОРМ.СТ.ОБР() и отложим их по вертикальной оси Y.

Если значения выборки , откладываемые по оси Х, взяты из стандартного нормального распределения , то на графике мы получим приблизительно прямую линию, проходящую примерно через 0 и под углом 45 градусов к оси х (если масштабы осей совпадают).

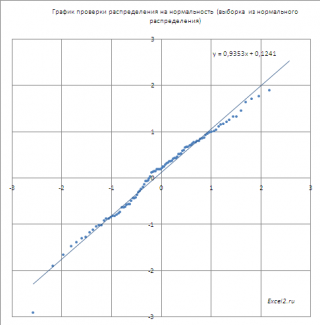
Расчеты и графики приведены в файле примера на листе Нормальное . О построении диаграмм см. статью Основные типы диаграмм в MS EXCEL .

Примечание : Значения выборки в файле примера сгенерированы с помощью формулы =НОРМ.СТ.ОБР(СЛЧИС()) . При перерасчете листа или нажатии клавиши F9 происходит обновление данных в выборке . О генерации чисел, распределенных по нормальному закону см. статью Нормальное распределение. Непрерывные распределения в MS EXCEL . Таже значения выборки могут быть сгенерированы с помощью надстройки Пакет анализа .

Если значения выборки взяты из нормального распределения (μ не обязательно равно 0, σ не обязательно равно 1), то угол наклона кривой даст оценку стандартного отклонения σ, а ордината точки пересечения оси Y – оценку среднего значения μ.

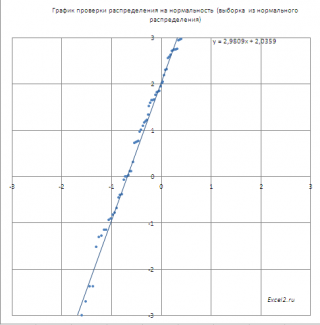
Данные оценки несколько отличаются от оценок параметров, полученных с помощью функций СРЗНАЧ() и СТАНДОТКЛОН.В() , т.к. они получены методом наименьших квадратов , рассмотренного в статье про регрессионный анализ.

Примечание : Рассмотренный выше метод в отечественной литературе имеет название Метод номограмм . Номограмма – это листы бумаги, разлинованные определенным образом. Номограмма используется в различных областях знаний. В математической статистике номограмма называется вероятностной бумагой. Такую «вероятностную бумагу» мы практически построили самостоятельно, когда нелинейно изменили масштаб шкалы ординат: =НОРМ.СТ.ОБР((j-0,5)/n)

Интересно посмотреть, как будут выглядеть на диаграмме данные, полученные из выборок из других распределений (не из нормального ). В файле примера на листе Равномерное приведен график, построенный на основе выборки из непрерывного равномерного распределения.

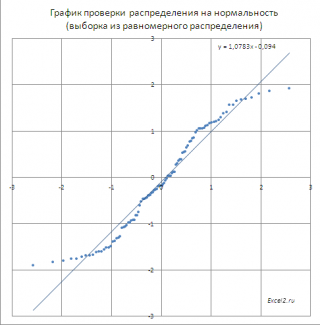
Очевидно, что значения выборки совсем не ложатся на прямую линию и предположение о нормальности выборки должно быть отвергнуто.

Подобная визуальная проверка выборки на соответствие другим распределениям может быть сделана при наличии соответствующих обратных функций . В статье Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL приведены графики для следующих распределений: Стьюдента , ХИ-квадрат распределения , F-распределения . Подобный график также приведен в статье про распределение Вейбулла .