Отрицательное Биномиальное распределение. Дискретные распределения в EXCEL
7 ноября 2016 г.
- Группы статей
- Распределения вероятностей
Рассмотрим Отрицательное Биномиальное распределение, вычислим его математическое ожидание и дисперсию. С помощью функции MS EXCEL ОТРБИНОМ.РАСП() построим графики функции распределения и плотности вероятности.
В основе Отрицательного Биномиального распределения (англ. Negative binomial distribution ) лежит Схема Бернулли , поэтому перед прочтением этой статьи целесообразно ее освежить в памяти, прочитав статью про Биномиальное распределение , где дано краткое пояснение схемы Бернулли .
Пусть проводятся испытания, в каждом из которых может произойти только 2 события: событие «успех» с вероятностью p или событие «неудача» с вероятностью q =1-p ( Схема Бернулли ).
Определим x как номер испытания, в котором был зарегистрирован r -й успех. В этом случае случайная величина x будет иметь Отрицательное Биномиальное распределение:
где r является целым числом =>1.
Как видно из определения, в Отрицательном Биномиальном распределении не установлен размер выборки , но зато заранее определена схема эксперимента: «до r-го успеха».
Примечание : Часто это распределение называют распределением Паскаля , а под Отрицательным Биномиальным распределением понимают его специальный случай, когда r не является целым числом, и r>0. Но, мы будем придерживаться терминологии MS EXCEL, в справке которого, распределение определено для целых r и называется Отрицательным Биномиальным распределением.
Другим специальным случаем этого распределения является распределение, где r всегда =1, т.е. такое x , при котором наблюдается первый успех. Это распределение называется Геометрическим распределением .
СОВЕТ : подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Примечание
: Запись
![]() означает количество сочетаний из
x-1
элементов по
r-1
. Для сочетаний также может использоваться эквивалентная запись
означает количество сочетаний из
x-1
элементов по
r-1
. Для сочетаний также может использоваться эквивалентная запись
![]() Подробнее о сочетаниях см. статью
Сочетания без повторений: Комбинаторика в MS EXCEL
.
Подробнее о сочетаниях см. статью
Сочетания без повторений: Комбинаторика в MS EXCEL
.
Отрицательное Биномиальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Отрицательного Биномиального распределения имеется функция ОТРБИНОМ.РАСП() , английское название NEGBINOM.DIST(), которая позволяет вычислить вероятность возникновения количества неудач до получения указанного количества успехов при заданной вероятности успеха.
Это определение несколько отличается от формулировки приведенной выше. Если количество неудач обозначить k, и учитывая, что k=x-r (общее количество испытаний минус количество успехов), то вышеуказанную формулу плотности вероятности можно переписать следующим образом:
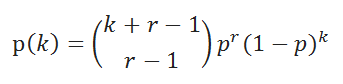
Именно это формула и лежит в основе функции ОТРБИНОМ.РАСП() (с точностью до обозначения: k нужно заменить на х ).
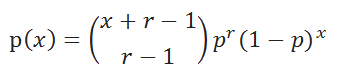
В файле примера на листе Пример приведен расчет плотности вероятности 2-мя способами. Естественно, оба способа возвращают одинаковый результат, но первый способ - через общее количество испытаний, воспринимается более естественно. Ниже все же используется подход, принятый в MS EXCEL: через количество неудач.
Чтобы вычислить функцию плотности вероятности p(x), см. формулу выше, необходимо установить четвертый аргумент в функции ОТРБИНОМ.РАСП() равным ЛОЖЬ. Для вычисления интегральной функции распределения (сумма вероятностей возникновения количества неудач от 0 до получения указанного количества «успехов» r ), необходимо установить четвертый аргумент равным ИСТИНА.
Примечание : До MS EXCEL 2010 в EXCEL была функция ОТРБИНОМРАСП() , которая позволяет вычислить только плотность вероятности . ОТРБИНОМРАСП() оставлена в MS EXCEL 2010 для совместимости. В файле примера приведена более сложная формула на основе функции ОТРБИНОМРАСП() и для вычисления интегральной функции распределения . Там же приведена формула для вычисления вероятности через определение (использована функция ЧИСЛКОМБ() ).
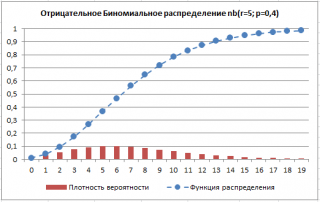
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения интегральной функции распределения идеально подходит диаграмма типа График , для плотности распределения – Гистограмма с группировкой . Подробнее о построении читайте статью Основные типы диаграмм .
Примечание : Для удобства написания формул в файле примера созданы Имена для параметров Отрицательного Биномиального распределения : r и p.
Примечание : В функции ОТРБИНОМ.РАСП() при нецелом значении х , дробная часть отбрасывается . Например, следующие формулы вернут одно и тоже значение: ОТРБИНОМ.РАСП( 2 ; 5; 0,4; ИСТИНА)= ОТРБИНОМ.РАСП( 2,9 ; 5; 0,4; ИСТИНА)
Задачи
Решения задач приведены в файле примера на листе Пример .
Задача1 . Нефтяная компания бурит скважины для добычи нефти. Вероятность обнаружить нефть в скважине равна 20%. Какова вероятность, что первая нефть будет получена с третьей попытки? Решение1 : =ОТРБИНОМ.РАСП(3-1;1;0,2;ЛОЖЬ)
Задача2 . Нефтяная компания бурит скважины для добычи нефти. Какова вероятность наличия 3-х нефтеносных скважин после бурения 7-й скважины. Вероятность обнаружить нефть в скважине равна 20%. Решение2 : =ОТРБИНОМ.РАСП(7-3;3;0,2;ЛОЖЬ)
Задача3 . Нефтяная компания бурит скважины для добычи нефти. Какова вероятность наличия 3-х нефтеносных скважин после бурения 7-ми скважин. Вероятность обнаружить нефть в скважине равна 20%. Решение3 : =ОТРБИНОМ.РАСП(7-3;3;0,2;ИСТИНА)
Показатели распределения
В файле примера на листе Пример имеются формулы для расчета математического ожидания = (1-p)*r/p и дисперсии (квадрата стандартного отклонения) =(1-p)*r/p^2.
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Комментарии