Геометрическое распределение. Дискретные распределения в EXCEL

Рассмотрим Геометрическое распределение, вычислим его математическое ожидание и дисперсию. С помощью функции MS EXCEL ОТРБИНОМ.РАСП() построим графики функции распределения и плотности вероятности.

Геометрическое распределение (англ. Geometric distribution ) является частным случаем Отрицательного Биномиального распределения (при r=1).

Пусть проводятся испытания, в каждом из которых может произойти только событие «успех» с вероятностью p или событие «неудача» с вероятностью q =1-p ( Схема Бернулли ).

Определим x как номер испытания, в котором был зарегистрирован первый успех. В этом случае случайная величина x будет иметь Геометрическое распределение:

СОВЕТ : подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .

Геометрическое распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для Отрицательного Биномиального распределения имеется функция ОТРБИНОМ.РАСП() , английское название NEGBINOM.DIST(), которая позволяет вычислить вероятность возникновения количества неудач до получения заданного числа успеха при заданной вероятности успеха.

Для Геометрического распределения второй аргумент этой функции должен быть 1, т.к. нас интересует только первый успех.

Это определение несколько отличается от формулировки приведенной выше, где вычисляется вероятность, что первый успех произойдет после x испытаний . Различие сводится к диапазону изменения диапазона x : если вероятность определена через количество испытаний, то х может принимать значения начиная с 1, а если через количество неудач, то – начиная с 0. Поэтому справедлива формула: p(x_ неудач )= p(x_ испытаний -1). См. файл примера лист Пример , где приведено 2 способа расчета.

Ниже используется подход, принятый в функции MS EXCEL: через количество неудач.

Чтобы вычислить функцию плотности вероятности p(x), см. формулу выше, необходимо установить четвертый аргумент в функции ОТРБИНОМ.РАСП() равным ЛОЖЬ. Для вычисления интегральной функции распределения , необходимо установить четвертый аргумент равным ИСТИНА.

Примечание : До MS EXCEL 2010 в EXCEL была функция ОТРБИНОМРАСП() , которая позволяет вычислить только плотность вероятности . В файле примера приведена формула на основе функции ОТРБИНОМРАСП() для вычисления интегральной функции распределения . Там же приведена формула для вычисления вероятности через определение.

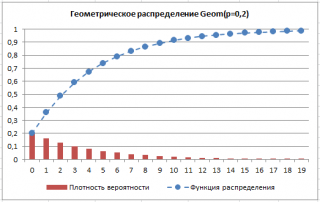
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .

Примечание : Для построения интегральной функции распределения идеально подходит диаграмма типа График , для плотности распределения – Гистограмма с группировкой . Подробнее о построении читайте статью Основные типы диаграмм .

Примечание : Для удобства написания формул для параметра p в файле примера создано Имя .

Примечание : В функции ОТРБИНОМ.РАСП( ) при нецелом значении х , дробная часть отбрасывается . Например, следующие формулы вернут одно и тоже значение: ОТРБИНОМ.РАСП( 2 ; 1; 0,4; ИСТИНА)= ОТРБИНОМ.РАСП( 2,9 ; 1; 0,4; ИСТИНА)

Задачи

Решения задач приведены в файле примера на листе Пример .

Задача1 . Нефтяная компания бурит скважины для добычи нефти. Вероятность обнаружить нефть в скважине равна 20%. Какова вероятность, что первая нефть будет получена именно в третью попытку? Какова вероятность, что для обнаружения первой нефти потребуется три попытки? Решение1 : =ОТРБИНОМ.РАСП(3-1; 1; 0,2; ЛОЖЬ) =ОТРБИНОМ.РАСП(3-1; 1; 0,2; ИСТИНА)

Задача2 . Рейтинговое агентство делает опрос случайных прохожих в городе о любимой марке автомобиля. Пусть известно, что у 1% горожан любимым автомобилем является Lada Granta . Какова вероятность, что встретить первого почитателя этой марки автомобиля после опроса 10 человек? Решение2 : =ОТРБИНОМ.РАСП(10-1; 1; 0,01; ИСТИНА )=9,56%

Задача3 . Рейтинговое агентство делает опрос случайных прохожих в городе о любимой марке автомобиля. Пусть известно, что у 1% горожан любимым автомобилем является Lada Granta. Сколько человек нужно опросить, чтобы вероятность, что встретить почитателя этой марки автомобиля была 50%? Решение3 : =ОТРБИНОМ.РАСП(L28-1; 1; 0,01; ИСТИНА) Изменяя значение ячейки L 28 с помощью Подбора параметра , необходимо добиться, чтобы результат формулы равнялся 0,5 (примерно).

Параметры распределения

В файле примера на листе Пример имеются формулы для расчета математического ожидания = (1-p)/p и дисперсии (квадрата стандартного отклонения) =(1-p)/p^2.

СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .