Скалярное произведение векторов в EXCEL, ортогональные векторы

Вычислим скалярное произведение векторов и проверим вектора на ортогональность. Подберем координаты вектора, ортогонального заданному, а также отобразим вектора в прямоугольной системе координат.

Скалярным произведением двух векторов называется действительное число (скаляр), равное произведению длин умножаемых векторов на косинус угла между ними.

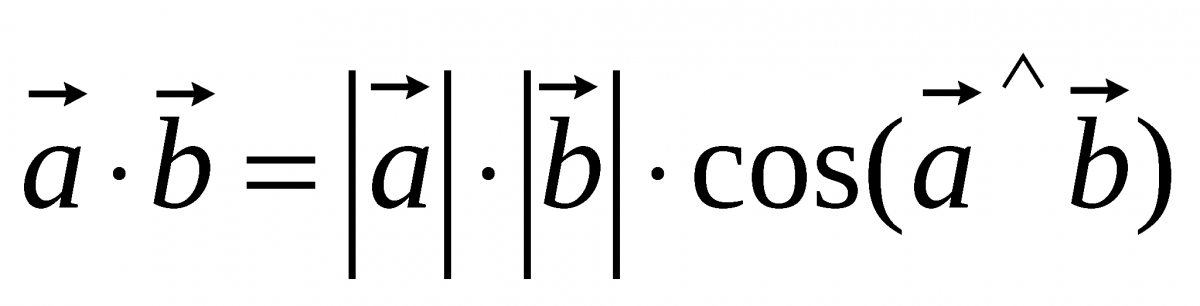
СОВЕТ : о нахождении длин векторов см. статью Вычисление длины (модуля) вектора в MS EXCEL .

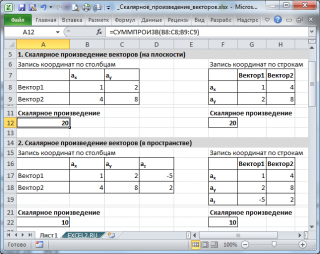
В случае двухмерной задачи скалярное произведение векторов a = { a _x ; a _y } и b = { b _x ; b _y } можно найти воспользовавшись следующей формулой: a · b = a _x · b _x + a _y · b _y Для вычисления скалярного произведения векторов в MS EXCEL идеально подходит функция СУММПРОИЗВ()

СОВЕТ : о функции СУММПРОИЗВ() см. статью Функция СУММПРОИЗВ() - Сложение и подсчет с множественными условиями в MS EXCEL

Если координаты 2-х векторов введены в диапазоны B8:C8 и B9:C9 соответственно, то формула =СУММПРОИЗВ(B8:C8;B9:C9) подсчитает скалярное произведение векторов (см. файл примера ).

Естественно, для трехмерного случая можно записать аналогичную формулу.

Ортогональность векторов

Два вектора называются ортогональными если угол между ними равен 90 градусов. Т.к. косинус угла 90 градусов равен 0, то и их скалярное произведение равно 0.

Интерес представляет поиск вектора, ортогонального заданному.

Поиск одной координаты. Сначала подберем одну из координат трехмерного вектора, так, чтобы он стал ортогональным заданному (2 другие координаты известны). Такая координата всегда существует и решение единственно.

Для нахождения третьей координаты будем использовать инструмент MS EXCEL Подбор параметра (подробнее см. Подбор параметра в MS EXCEL ).

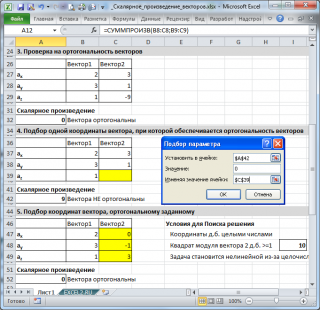
Пусть координаты заданного вектора равны {2; 3; 1} (и размещены в ячейках В37:В39 ), а известные координаты искомого ортогонального вектора равны  {3; 1; ?} (размещены в ячейках С37:С39 ) См. рисунок выше и файл примера .

Вычислим в ячейке А42 скалярное произведение векторов с помощью формулы =СУММПРОИЗВ(B37:B39;C37:C39)

Вызовем окно Подбора параметра для ввода критериев поиска и установим их как показано на рисунке выше. После нажатия кнопки ОК в ячейке С39 (искомая координата) будет введено значение -9, а скалярное произведение станет равно 0.

Поиск всех координат ортогонального вектора. Если заданы координаты только исходного вектора и требуется определить все 3 координаты вектора, ортогональному к нему, то, понятно, что решение не единственно.

Например, для двухмерного случая (на плоскости), можно построить 2 разных вектора, которые будут ортогональны заданному (точнее не 2, а бесконечное множество коллинеарных векторов в двух противоположных направлениях).

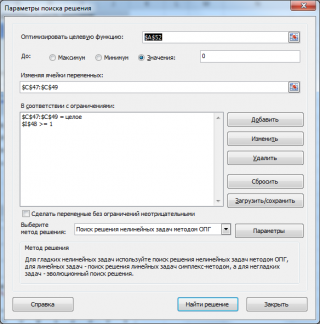
Так как нам придется одновременно подбирать сразу 3 координаты, то Подбор параметра нам не подходит, нужно использовать Поиск решения (См. файл примера) .

В качестве ограничений для Поиска решения можно установить: найденные координаты должны быть целыми числами, а квадрат модуля искомого вектора д.б. >1 (иначе 0 вектор будет предложен в качестве решения). Также можно наложить ограничение на максимальную длину вектора.

После запуска инструмента Поиск решения будут найдены координаты {0; -1; 3}

Отображение (ортогональных) векторов на плоскости

В двухмерном случае можно отобразить 2 ортогональных вектора.

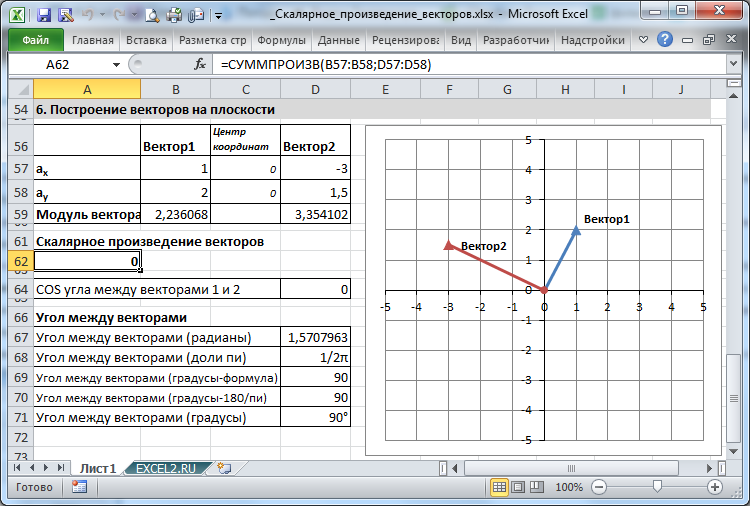
Тип диаграммы установлен График (см. Основные типы диаграмм в MS EXCEL , раздел График).

Чтобы вектора выглядели ортогональными, необходимо зафиксировать минимальные и максимальные значения, отображаемые осями (см. Основы построения диаграмм в MS EXCEL , раздел 7.Оси), иначе при построении различных пар векторов MS EXCEL будет применять автомасштабирование графика и масштабы осей могут стать не равными (это приведет к тому, что угол 90 градусов не будет выглядеть прямым).