Поиск решения EXCEL (6.5). Пропускная способность сетевого трубопровода

Необходимо найти максимальную пропускную способность сетевого трубопровода. Построим линейную модель и с помощью надстройки Поиск решения решим задачу.

Задача

Имеется 8 узлов нефтетрубопровода, которые соединены между собой. Один из узлов – Источник (Исток), еще один – Сток, куда стекаются все нефтепродукты сети. У каждой ветви трубопровода имеется своя пропускная способность (ПС). Необходимо определить загрузку каждой ветви трубопровода, при которой суммарный входящий поток на узел Сток – максимален.

Создание модели

Теперь создадим линейную модель для решения задачи с помощью Поиска решения .

Совет : Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .

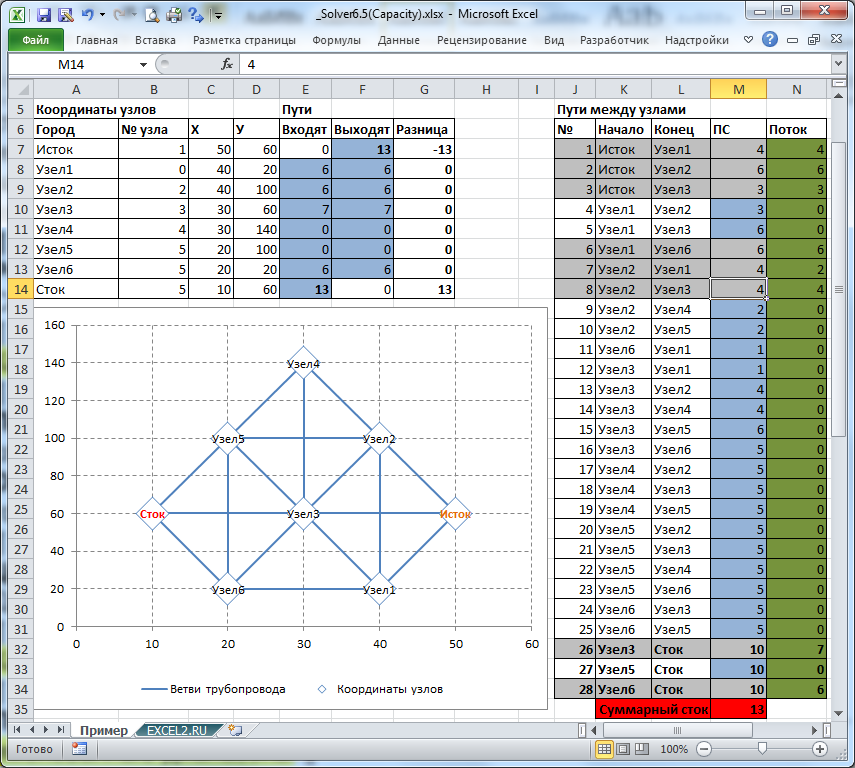
Переменные (выделено зеленым) . В качестве переменных модели следует взять величину потока каждой ветви трубопровода. Ограничения (выделено синим) . Необходимо, чтобы из каждого узла величины входящих и исходящих потоков были равны. Для узла Исток определены только исходящие потоки, для Сток – только входящие: эти величины должны быть равны. Целевая функция (выделено красным) . Пропускная способность сети трубопроводов должна быть максимальной (суммарный поток, идущий в Сток, должен быть максимальным).

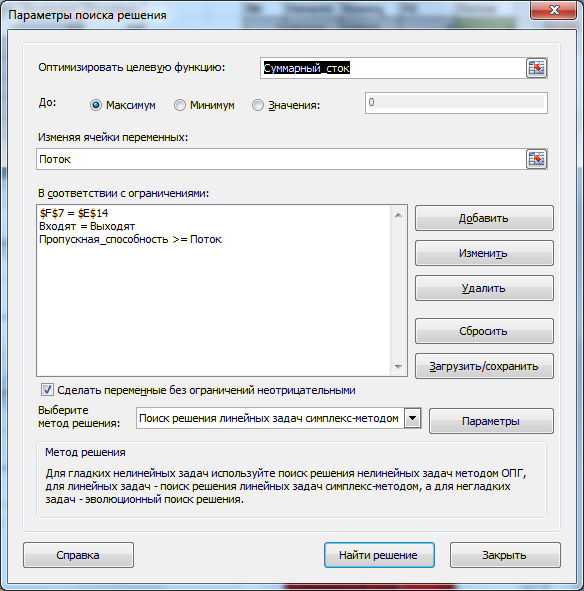
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .

Выберите Линейный метод поиска решения, т.к. созданная модель является линейной.

Найденное Решение

Поиск решения распределит потоки между узлами сети так, чтобы соблюсти все ограничения и максимизировать поток. С помощью этой модели можно найти не только максимальную общую пропускную способность сети, но и отдельные потоки и их направление по отдельным дугам, а также минимальный разрез – это совокупность дуг, которые определяют «узкое место» (bottleneck), которое ограничивает общую пропускную способность сети.

Совет . В статье Поиск решения MS EXCEL (6.6). Минимальные затраты транспортной сети решена задача нахождения маршрутов, при которых затраты на функционирование сети минимальны. В статье Поиск решения MS EXCEL (6.4). Кратчайший путь (неполный граф, линейная модель) рассмотрена задача по определению кратчайшего пути (на основе вышерассмотренной транспортной сети).