Перед прочтением данной статьи рекомендуется ознакомиться с Аннуитетной схемой погашения кредита. В статье по этой ссылке приведены функции аннуитета, их параметры и принятые обозначения, которые будут использоваться в данной статье (ПЛТ - ежемесячный платеж, n - количество периодов, r - ставка по кредиту за период и др.).

Решаемая задача

Рассчитаем график погашения кредита, который гасится не по чистой схеме аннуитета (регулярные равные платежи), а с кредитными каникулами и с баллонным платежом. Баллонный платёж — это крупный платёж, который покрывает основную сумму долга в конце срока. В нашей схеме мы сделаем возможность расчета в случае когда Баллонный платёж платится в произвольный период. Помимо этого, учтем, что банк может взимать проценты как в начале, так и в конце каждого периода. Кроме того, в нашем графике платежей учтем еще и ежемесячный дополнительный постоянный платеж, он обычно представляет собой страховку в пользу банка.

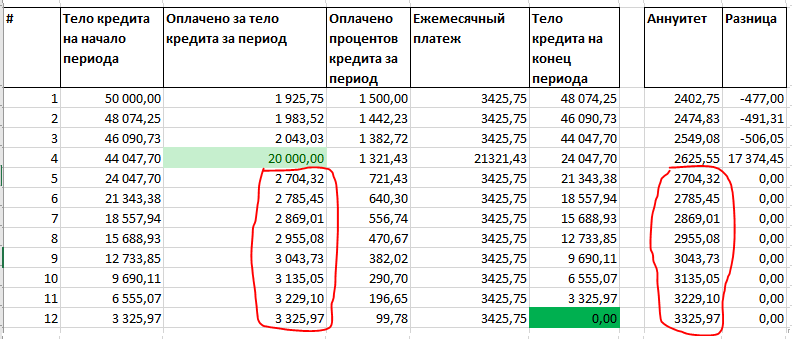
В итоге мы получим вот такой график

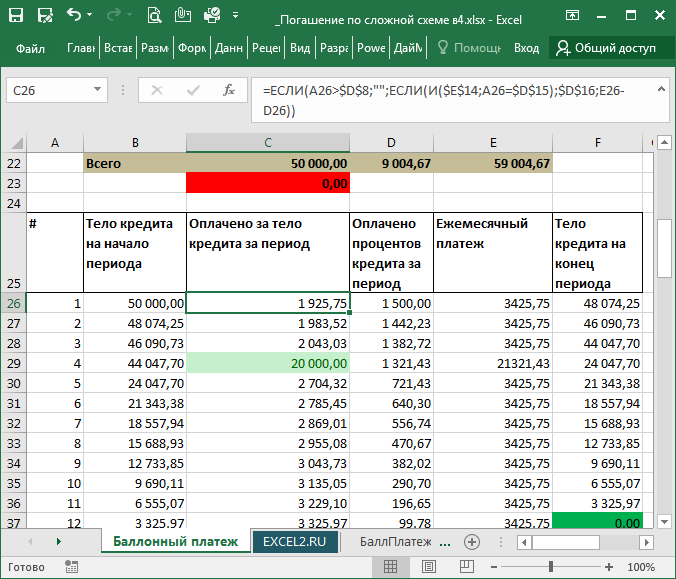
Данный график будет автоматически рассчитываться относительно простыми формулами на основе исходных данных (см. желтые ячейки):

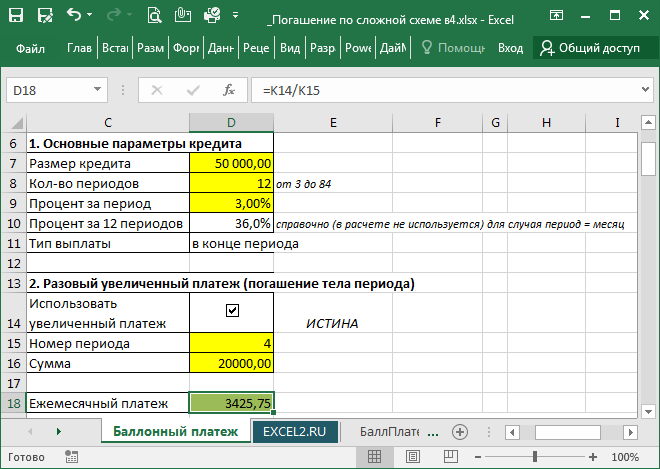
Примечание: кредит с баллонным платежом также называют Шаровой кредит или Кредит-баллун. Такие кощунственные для русского языка названия происходят из-за прямолинейного перевода с английского (Finance Lease with Balloon Payment). Схемы с Баллонным платежом часто используются в лизинге.

График погашения кредита с Баллонным платежом базируется на формулах аннуитета, поэтому коротко вспомним некоторые нюансы, которые будем использовать при расчетах.

Коротко об Аннуитете

Аннуитетная схема погашения кредита хорошо известна всем, кто хоть раз брал кредит и при этом задумывался о доле ежемесячного платежа, которая идет на погашение тела кредита. Например, если кредит берется на 3 года (36 периодов) по годовой ставке 36% (3% в месяц), то в первые периоды на погашение основной суммы долга идет около 1/3 ежемесячного платежа (остальное на погашение процентов). Т.е. задолженность снижается медленно (за 1 год, т.е. за 1/3 срока, будет погашено только около 22% долга). Зато в последние периоды около 90% ежемесячного платежа идет на погашение основной суммы долга (банк уже забрал все проценты).

Почему же так получается? В статье Аннуитет. Расчет периодического платежа в EXCEL. Погашение ссуды (кредита, займа), точнее в файле примера на листе Аннуитет (без ПЛТ), приведена формула для расчета суммы, которая идет на погашение основного долга в каждый период i.

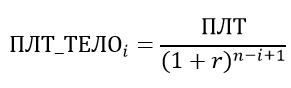
Теперь очевидно, что в первый период доля ежемесячного платежа, идущая на оплату основной суммы долга, будет составлять лишь 1/(1+0,03)³⁶, т.е. 0,34, что приблизительно равно 1/3.

Очевидно, что сумма всех ПЛТ_ТЕЛО должна быть равна величине кредита (обозначим ПС - сумму кредита. ПС - это от Приведенная стоимость). Также заметим, что все ПЛТ_ТЕЛО соседних периодов отличаются на один и тот же коэффициент 1/(1+r). А это означает, что сумма всех ПЛТ_ТЕЛО представляет собой сумму геометрической прогрессии. Воспользовавшись школьной формулой можно получить формулу, связывающую основные параметры аннуитета:

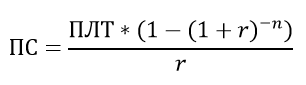
Примечание: в вышеуказанной формуле есть 2 предположения: проценты платятся в конце периода и в последний период долг полностью погашается. 

Соответственно, формула для вычисления ежемесячного платежа выглядит так:

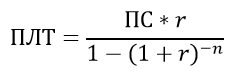
Примечание: в классическом аннуитете ПЛТ имеет противоположный знак с ПС, чтобы подчеркнуть разнонаправленность платежей: +ПС - банк предоставляет вам кредит, -ПЛТ - вы возвращаете банку сумму кредита и %. Для целей данной статьи минус в формуле указывать не будем.

Определяем ежемесячный платеж в схеме с Баллонным платежом

Чтобы построить график платежей нам потребуется вычислить ежемесячный платеж (ПЛТ-штрих или ПЛТ'), т.е. аннуитетный ПЛТ скорректированный с учетом Баллонного платежа. В этом разделе будем выводить формулу ежемесячного платежа.

Пусть Баллонный платеж происходит в период i=z. В примере ниже z=4, а всего будет n=12 периодов.

Можно показать, что платежи, которые идут на погашение тела кредита в обоих схемах (классического аннуитета и схемы с баллонным платежом) одинаковы, но только после собственно Баллонного платежа.

Примечание: правда, для этого нам потребуется иметь рассчитанный график с Баллонным платежом.

Это хорошая новость, т.к.:

1. ПЛТ_ТЕЛО'_i = ПЛТ_ТЕЛО_i (классический аннуитет остается в силе для i>z)
2. Cумму ПЛТ_ТЕЛО'_i, начиная с периода z+1, можно вычислить используя формулу суммы геометрической прогрессии.

Но, что из себя представляют ПЛТ_ТЕЛО'_i для периодов, которые до баллонного платежа (i<z)? Опять хорошая новость, это тоже члены геометрической прогрессии, которые отличаются на один и тот же коэффициент 1/(1+r). Однако, они несколько меньше, чем ПЛТ_ТЕЛО'_i для i>z. 

Почему они меньше? Дело в том, что до выплаты большого Баллонного платежа сумма задолженности остается большой, что приводит к повышенным процентам за период, и, соответственно, доля платежа, идущая в погашение основной суммы долга, снижается относительно классического аннуитета. Это снижение можно выразить через коэффициент k, который содержат все ПЛТ_ТЕЛО'_i для i<z. Таким образом, для i<z ПЛТ_ТЕЛО'_i = k * ПЛТ_ТЕЛО_i 

Если обозначить Баллонный платеж как P', то формулу для суммы кредита (ПС) в нашем случае (n=12, z=4) можно написать следующим образом:

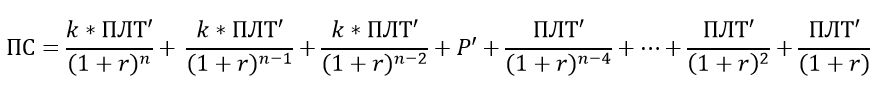
У нас 2 неизвестных (ПЛТ' и k), но только одно уравнение. Чтобы найти ПЛТ' нужно еще одно уравнение. Воспользуемся расчетами первого периода:

• проценты за период равны ПС*r
• ПЛТ_ТЕЛО'₁ = k * ПЛТ' / (1+r)ⁿ

Сумма ПС*r и ПЛТ_ТЕЛО'₁ равна ПЛТ'. Вот и недостающее уравнение, из которого можно выразить k через ПЛТ'.

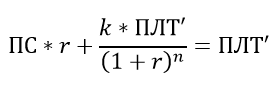
Осталось аккуратно вычислить 2 суммы геометрических прогрессий: для  i<z и  i>z. Для i<z всего членов будет z-1, обозначим N₁. Для i>z всего членов будет n-z, обозначим N₂.

Для членов с i<z за скобки можно вынести одинаковый коэффициент k * ПЛТ' / (1+r)^n-z+2, а для  i>z за скобки можно вынести ПЛТ'/(1+r). После этого в обоих случаях первые члены последовательностей станут равны 1. Обозначим n-z+2 как m.

Подробный вывод формулы приводить не будем, запишем промежуточный вариант:

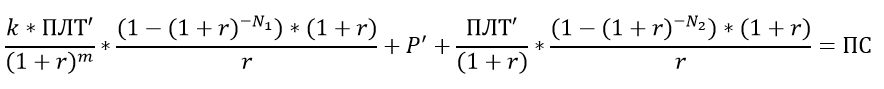
и, наконец, итоговый результат:

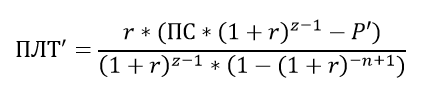
Как и ожидалось, формула слегка напоминает формулу для классического аннуитета, но появились 2 переменных: величина P' и период z Баллонного платежа. Если P' указать =0, а степень -n+1 заменить на -n, то формула превратится в формулу для классического аннуитета.

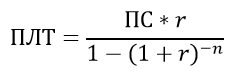
Расчет ПЛТ', а равно как и графика платежа приведен в файле примера на листе Баллонный платеж. При изменении исходных данных в желтых ячейках (P', n, z, ПС, r) значение ежемесячного платежа ПЛТ' автоматически пересчитывается. 

Расчет графика платежа для более сложного случая 

Для более сложного случая, когда помимо баллонного платежа есть еще и кредитные каникулы (платим только проценты, основную сумму долга не погашаем), а также имеется ежемесячная страховка и опция начисления процента в конце или начале периода, то вывод формулы получится более сложным. Самое время воспользоваться мощью EXCEL для подбора такого платежа, который бы соответствовал всем условиям в желтых ячейках.

График платежа для данного случая приведен в файле примера на листе БаллПлатеж+каникулы.

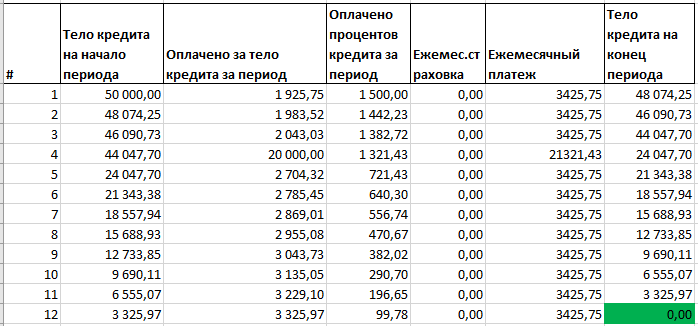
Для одинаковых условий оба метода расчета, естественно, совпадают.

В случае наличия каникул в 7 и 8 периоде график выглядит следующим образом (также добавлена ежемесячная страховка=100):

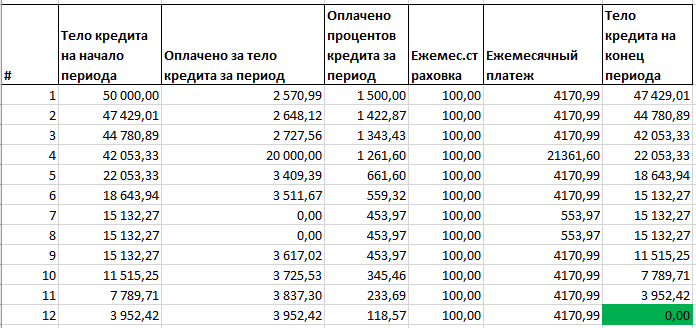
Формально, в файле примера не задействован инструмент EXCEL Подбор параметра (хотя мог бы). Дело в том, что в этом случае его нужно было бы перезапускать каждый раз при изменении исходных данных, а это не удобно. Конечно, макрос бы исправил дело, но есть и другой вариант. 

При подборе ПЛТ' EXCEL будет стремиться подобрать такой ПЛТ', при котором сумма оплат тел кредита в каждом периоде (ПЛТ_ТЕЛО_i) равнялась бы ПС (сумме кредита). Это не сложно настроить, заставив EXCEL изменять значение в зеленой ячейке, пока значение в красной не станет равной 0. 

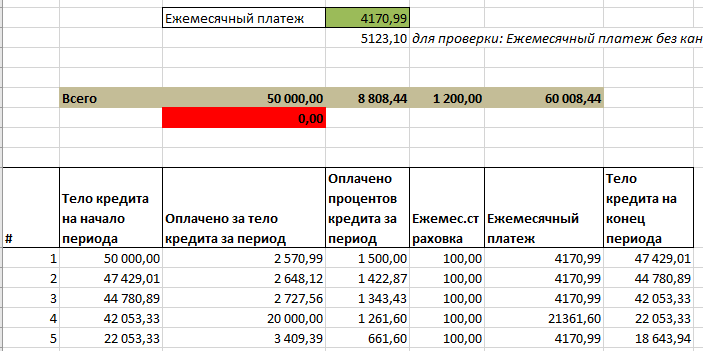
Вполне предсказуемо, что зависимость значения в красной ячейке от ПЛТ' является линейной (ПС линейно зависит от ПЛТ' в каждой из выше указанных формул). Зная эту зависимость, можно рассчитать ПЛТ'. Формулу линейной зависимости Y=a*X+b можно вычислить зная координаты 2х любых точек. 

В файле примера в служебных столбцах создано 2 таблицы для 2х произвольных значениях ПЛТ' равных 0 и 500 соответственно. Далее, вычислив  tg угла наклона и пересечение с осью ординат, получим уравнение прямой. Задав Y=0, получим Х, т.е. ПЛТ'.