Вычислим в MS EXCEL определенный интеграл методом Симпсона (англ. Simpson's rule). Покажем как оценить ошибку интегрирования, построим график функции.

Примечание: Основная статья про численное интегрирование - Интегрирование в MS EXCEL. Метод трапеций. В этой статье дана небольшая теория.

В данной статье используем тот же полином третьего порядка, что и в статье про Метод трапеций. Т.к. метод Симпсона использует параболу для аппроксимации подинтегральной функции, то при нахождении этим методом интеграла от полинома третьего порядка (и ниже) мы будем получать точное значение (это можно доказать строго математически). Т.е. ошибка интегрирования точно равна 0. 

Построение модели

Для определенности вычислим интеграл для функции-многочлена f(𝑥)=𝑥³−5𝑥²+6𝑥+1. График этой функции в диапазоне от 0 до 4 выглядит следующим образом (см. файл примера).

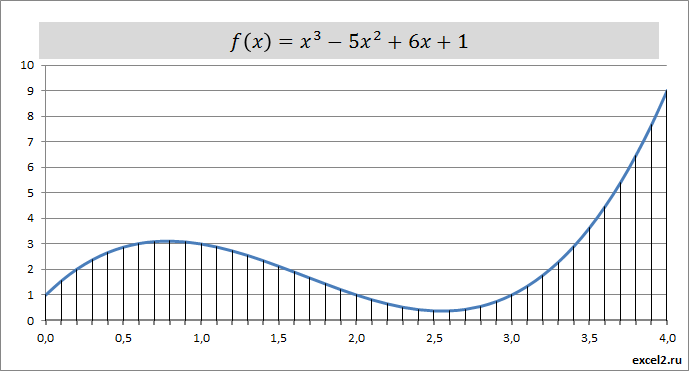
Примечание: про тонкости построения графика функции можно прочитать в этой статье https://excel2.ru/articles/grafik-vs-tochechnaya-diagramma-v-ms-excel.

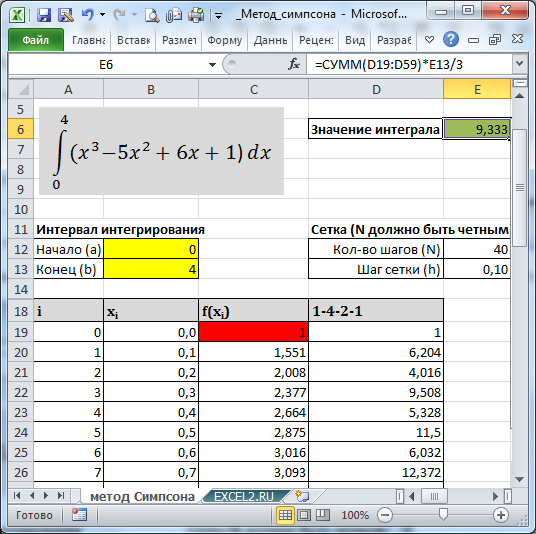
В файле примера построим таблицу значений функции для 41 точки (от 0 до 40), что составляет 40 интервалов (для метода Симпсона обязательно должно быть ЧЕТНОЕ количество интервалов).

Формула для вычисления интеграла Методом Симпсона следующая:

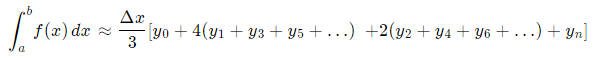
Примечание: В файле примера вместо Δх (шаг по х) будем использовать символ h, который используется в математических формулах численного интегрирования гораздо чаще, чем Δх. Хотя для первого знакомства, конечно, Δх является более знакомым обозначением шага изменения х.

Как видно из формулы, чтобы вычислить значение интеграла достаточно сложить значения y=f(x) в узлах сетки с определенным весом:

• Значения в узлах 0 и n, которые соответствуют пределам интегрирования а и b, берутся с весом 1;
• Значения в узлах с нечетным индексом берутся с весом 4;
• Значения в узлах с четным индексом берутся с весом 2.

В MS EXCEL вычислить веса по этому правилу можно с помощью простой формулы =ЕСЛИ(ИЛИ(A19=0;A19=$E$12);1; ЕСЛИ(ЕНЕЧЁТ(A19);4;2)). В файле примера это реализовано в столбце D (дополнительно вес домножен на соответствующее значение y).

В итоге, значение определенного интеграла, вычисленное по методу Симпсона, можно записать простой формулой =СУММ(D19:D59)*E13/3

Вычислив интеграл аналитически, можно убедиться, что полученное значение точно равно значению, вычисленного формулами (напомним, что это справедливо только для полиномов не выше третьего порядка).

Ошибка интегрирования

Формула для оценки ошибки интегрирования основана на вычислении 4-й (!) производной, что достаточно трудоемко и совсем не удобно для реализации в MS EXCEL. 

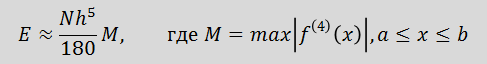
После вычисления 4-й производной подинтегральной функции нужно найти ее максимум в интервале интегрирования, а затем подставить в вышеуказанную формулу. Понятно, что для полиномов не выше третьего порядка оценка будет равна 0, а значит точность метода Симпсона для таких функций выше чем Метод трапеций.

Для более сложных функций нахождение 4-й производной будет трудоемко, но к счастью есть много сайтов, которые помогут в этом вопросе, например https://www.derivative-calculator.net/ 

Настраиваемый интервал

На листе Настраиваемый интервал сделана удобная форма для вычисления интеграла при различных значениях шага интегрирования. График функции также перестраивается динамически благодаря использованию Имен и функции СМЕЩ().

Данная форма удобна когда необходимо ответить на вопрос "Какой шаг сетки нужно выбрать, чтобы точность интегрирования была не хуже заданному значению?". Правда, для этого потребуется вычислить 4-ю производную, найти максимум этой функции и, наконец, по формуле оценить ошибку.

Лирическое отступление

Зачем оценивать ошибку интегрирования? Можно ведь взять "маленький" шаг сетки и заведомо получить "точный" результат, и не важно что потребуется сделать 1000 или более шагов интегрирования, ведь вычислительные мощности так дешевы! 

На этот счет есть 2 замечания: для больших интервалов интегрирования может потребоваться слишком много шагов и если вычисление интеграла лишь часть задачи, да еще и если оно находится в цикле, то это может замедлить работу программы. И второй момент: если мы не знаем ошибки, то как мы можем быть уверены, что вычисленное значение нам подходит? Например, мы вычисляем интеграл, чтобы получить значение, которое мы будем затем сравнивать с неким критерием. Если значение больше критерия, то мы принимаем одно решение, а если нет, то другое. Из-за недостаточной точности вычисления интеграла может случиться, что будет принято неверное решение, что соответственно приведет к некорректной работе программы (в определенной ситуации).