Генерация дискретного случайного числа с произвольной функцией распределения в EXCEL

Пусть задана некая (пользовательская) функция распределения дискретной случайной величины. Сгенерируем случайное число из этой генеральной совокупности. Также рассмотрим функцию ВЕРОЯТНОСТЬ() .

Перед прочтением данной статьи рекомендуется освежить в памяти понятие Функция распределения случайной величины .

Часто случайная величина моделируется определенным распределением. Например, вес куска мыла, изготавливаемого на фабрике, может быть распределен по нормальному закону , а число автомобилей, прибывающих на стоянку в определенный период времени - распределению Пуассона .

Однако, бывают ситуации, когда форма распределения неизвестна, известно лишь, что дискретная случайная величина принимает некие значения с определенной вероятностью. Назовем такую функцию распределения "произвольной" функцией распределения , т.е. которая не соответствует известным законам распределения, а задана пользователем из опыта.

Зададим вероятности, что дискретная случайная величина Х примет определенное значение, с использованием таблицы (см. файл примера ).

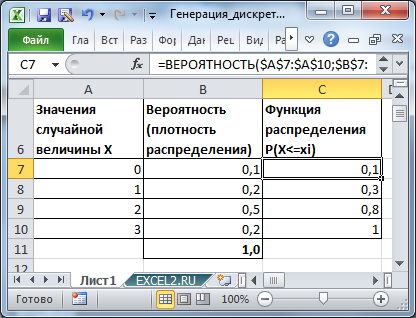
Для вычисления Функции распределения используем функцию ВЕРОЯТНОСТЬ() .

Формула =ВЕРОЯТНОСТЬ($A$7:$A$10;$B$7:$B$10;$A$7;A7) вернет Функцию распределения . Того же результата можно добиться с помощью формулы =СУММ($B$6:B7) .

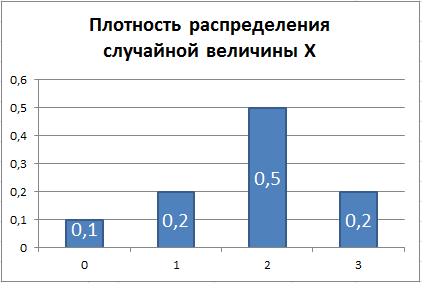
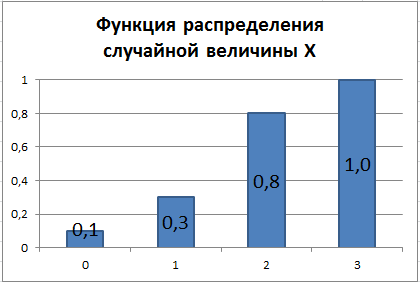
Функция ВЕРОЯТНОСТЬ() удобна тем, что она выполняет проверку:

• сумма вероятностей в столбце В должна быть равна 1;
• вероятность для каждого значения должна быть в пределе от 0 до 1;
• количество значений должно соответствовать вероятностям (в нашем случае 4 значениям случайной величины сопоставлены 4 значения вероятности).

Для генерации случайного числа создадим дополнительный столбец E .

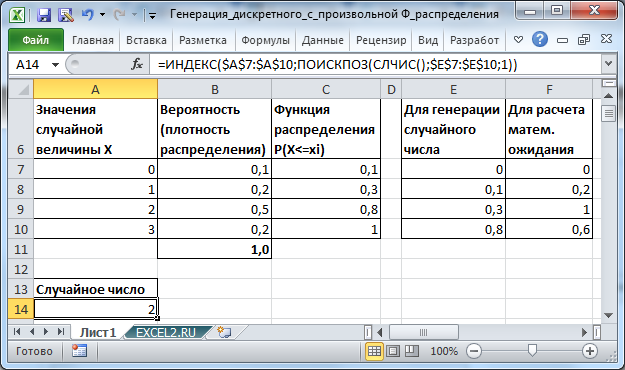
Этот столбец практически совпадает со значениями функции распределения, но он начинается с 0 и не содержит 1.

Теперь запишем формулу для генерации случайного числа:

=ИНДЕКС($A$7:$A$10;ПОИСКПОЗ(СЛЧИС();$E$7:$E$10;1))

Разберем ее работу:

• Функция СЛЧИС() возвращает равномерно распределенное случайное число в интервале от 0 до 1 (см. эту статью ). Результат соответствует вероятности (ось y на графике функции распределения);
• Функция ПОИСКПОЗ () возвращает позицию из диапазона Е7:Е10 , в которой содержится наименьшее значение <= результату функции СЛЧИС() . Т.е. если СЛЧИС() вернула 0,5, то результат функции будет 3 (т.к. наименьшее число, которое <=0,5 - это 0,8, а 0,8 - содержится в 3-й строке диапазона Е7:Е10 ). Подробнее о функции ПОИСКПОЗ() см. в статье Функция ПОИСКПОЗ() в MS EXCEL ;
• Функция ИНДЕКС () возвращает значение из диапазона A7:A10, у которого позиция совпадает с найденной функцией ПОИСКПОЗ() . Подробнее о функции ИНДЕКС () см. в статье Функция ИНДЕКС() в MS EXCEL .

Почему это работает? Рассмотрим интервал между 0,3 и 0,8, который равен половине интервала вероятностей (т.е. равен 0,5). На графике плотности вероятности видно, что этот интервал соответствует числу 2. Следовательно, результат функции СЛЧИС() будет в среднем в 50% случаях соответствовать именно этому числу.

Чтобы убедиться в этом, вычислим математическое ожидание нашего распределения =СУММ(F7:F10) . Оно равно 1,8. Теперь сгенерируем массив случайных чисел в столбце W и вычислим оценку среднего (математического ожидания). В файле примера видно, что оценка, вычисленная по формуле =СРЗНАЧ(W6:W55) , близка к истинному значению 1,8.

Задача

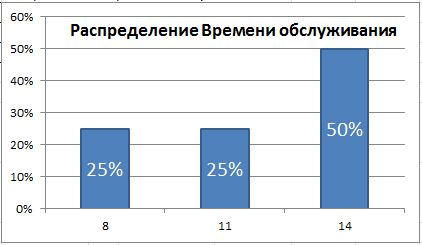
Для 50% покупателей время обслуживания 14 минут, для 25% - 8 минут и для оставшихся 25% - 11. Используя функцию СЛЧИС() сделать генератор, который будет случайно выдавать значения в этом интервале.

Решением вышеуказанной задачи является формула = ВПР(СЛЧИС();{0;14:0,5;11:0,75;8};2)

Если случайное число меньше 0,5 (50%), то время обслуживания составляет 14 минут, если от 0,5 до 0,75 (25%), то 11 минут, если от 0,75 до 1, то 8 минут (см. файл примера ).

Вместо {массива констант} в формуле можно использовать ссылку на диапазон ячеек: в одном столбце 0; 0,5; 0,75 (проценты), в другом - 14; 11; 8 (минуты).

Примечание : Про функцию ВПР() можно прочитать здесь .

СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .