Векторное произведение в EXCEL

Найдем векторное произведение 2-х векторов с помощью функций MS EXCEL. Также создадим таблицу для проверки векторов на коллинеарность.

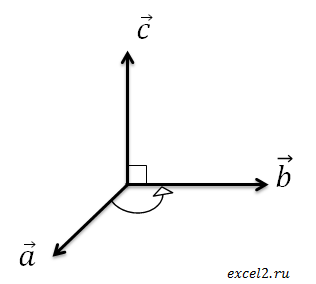
Сначала немного теории. Векторным произведением двух векторов а и b , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор c , что:

1. он перпендикулярен обоим векторам а и b ;
2. длина вектора с равна произведению длин векторов а и b на синус угла между ними;
3. вектор с направлен так, что тройка векторов а , b и с является правой ( с конца вектора с кратчайший поворот от вектора a к вектору b виден наблюдателю против часовой стрелки ).

Почему такое сложное определение? Дело в том, что результатом векторного произведения [ a х b ], в отличие от скалярного , является вектор. А для того, чтобы однозначно определить вектор нужно задать его длину (второй пункт определения) и направление (первый и третий пункты определения).

Векторное произведение двух векторов a = { a _x ; a _y ; a _z } и b = { b _x ; b _y ; b _z } в декартовой системе координат можно вычислить, используя формулы:

[ a х b ] = { a _y b _z - a _z b _y ; a _z b _x - a _x b _z ; a _x b _y - a _y b _x }

или в матричной форме:

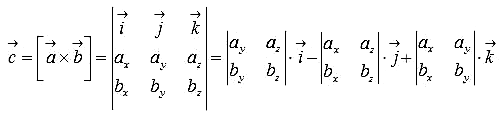
Теперь вычислим векторное произведение в MS EXCEL. Встроенная функция к сожалению отсутствует. Кроме того, формула должна возвращать три значения, т.е. 3 координаты вектора. Это может быть реализовано только формулой массива (вариант, когда 3 координаты рассчитываются независимо, с использованием 3-х различных формул, очевиден, но не интересен, хотя и приведен файле примера ).

Пусть даны координаты векторов а и b , записанные в строках 8 и 9 (см. файл примера ).

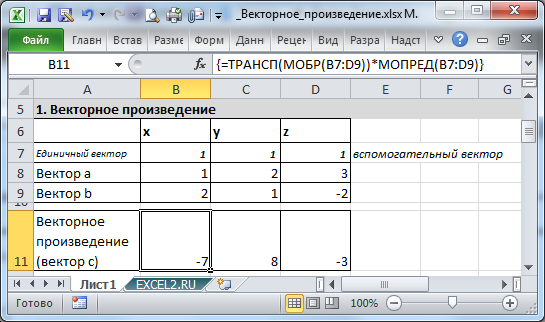
Обратим внимание, что запись в матричной форме напоминает вычисление обратной матрицы методом алгебраических дополнений . Вместо единичных векторов i, j, k запишем вспомогательный вектор с координатами {1; 1; 1} и поместим его в строке 7 над векторами. Теперь у нас есть квадратная матрица А третьего порядка, для которой можно вычислить обратную матрицу.

Попробуем использовать функцию МОБР() для вычисления векторного произведения. Заметим, что три слагаемых из определения векторного произведения в матричной форме совпадают со значениями верхней строки матрицы алгебраических дополнений.

Примечание : Напомним, что алгебраическое дополнение A _ij вычисляется по формуле A _ij =(-1) ^i+j *М _ij (где М - соответствующий минор, т.е. определитель, состоящий из элементов матрицы А за исключением всех элементов, расположенных на строке i и в столбце j).

Так как обратная матрица вычисляется по формуле:

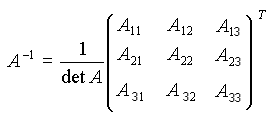
то имея обратную матрицу, для вычисления верхней строки матрицы алгебраических дополнений и, соответственно, координат вектора с , необходимо ее транспонировать , а затем умножить ее на определитель матрицы А (той, что содержит координаты наших векторов а и b и единичный вектор).

Это реализовано с помощью формулы массива =ТРАНСП(МОБР(B7:D9))*МОПРЕД(B7:D9)

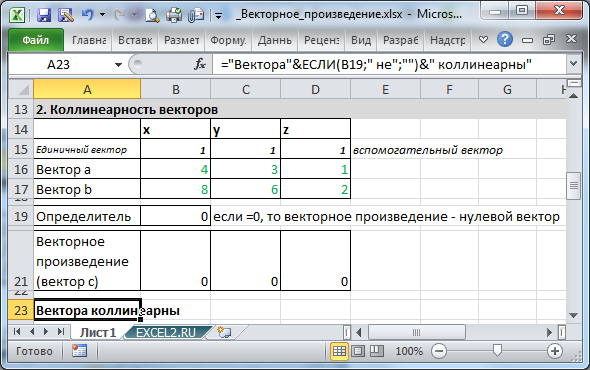
Коллинеарность векторов

Если два вектора коллинеарны, т.е. лежат на параллельных прямых, то их векторное произведение равно 0. В файле примеров приведена таблица для проверки векторов на коллинеарность.

Нахождение длины вектора с - результата векторного произведения

Из определения векторного произведения длина вектора с равна произведению длин векторов а и b на синус угла между ними.

Примечание : Как вычислить длины векторов по их координатам показано в статье Вычисление длины (модуля) вектора в MS EXCEL .

Синус угла найдем через тригонометрическую формулe sin ² x+cos ² x=1

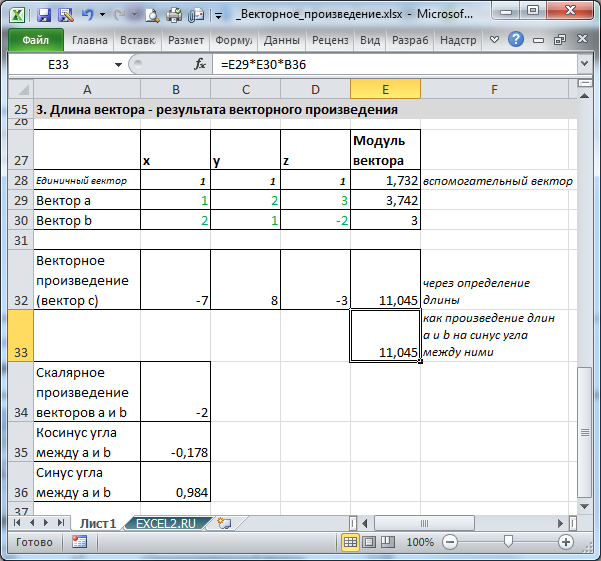
Конечно, можно также сначала найти векторное произведение, а затем длину полученного вектора. Естественно, оба метода расчета дают одинаковые результаты.