Вычисление определителя матрицы в EXCEL

Вычислим определитель (детерминант) матрицы с помощью функции МОПРЕД() или англ. MDETERM, разложением по строке/столбцу (для 3 х 3) и по определению (до 6 порядка).

Определитель матрицы (det) можно вычислить только для квадратных матриц, т.е. у которых количество строк равно количеству столбцов.

Для вычисления определителя в MS EXCEL есть специальная функция МОПРЕД() . В аргументе функции необходимо указать ссылку на диапазон ячеек (массив), содержащий элементы матрицы (см. файл примера ).

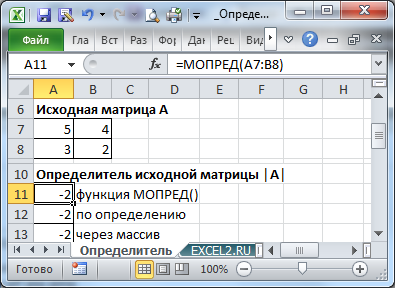
Массив может быть задан не только как интервал ячеек, например A7:B8 , но и как массив констант , например =МОПРЕД({5;4:3;2}) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.

Ссылка на массив также может быть указана как ссылка на именованный диапазон .

Для матриц порядка 2 можно определитель можно вычислить без использования функции МОПРЕД() . Например, для вышеуказанной матрицы выражение =A7*B8-B7*A8 вернет тот же результат.

Для матрицы порядка 3, например размещенной в диапазоне A16:C18 , выражение усложняется =A16*(B17*C18-C17*B18)-B16*(A17*C18-C17*A18)+C16*(A17*B18-B17*A18) (разложение по строке).

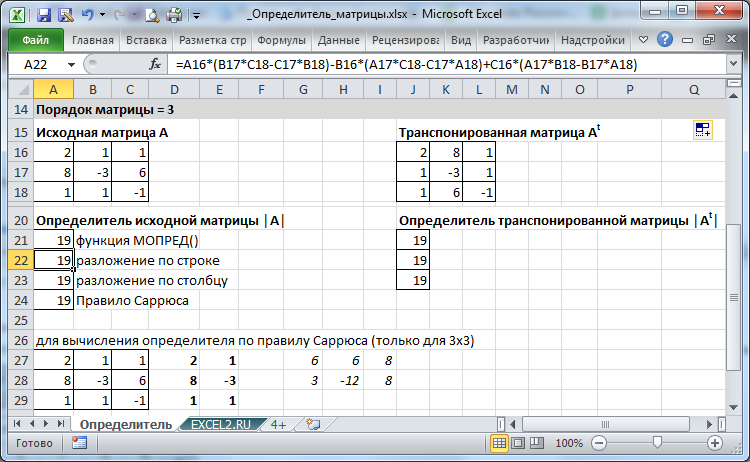
В файле примера для матрицы 3 х 3 определитель также вычислен через разложение по столбцу и по правилу Саррюса.

Свойства определителя

Теперь о некоторых свойствах определителя (см. файл примера ):

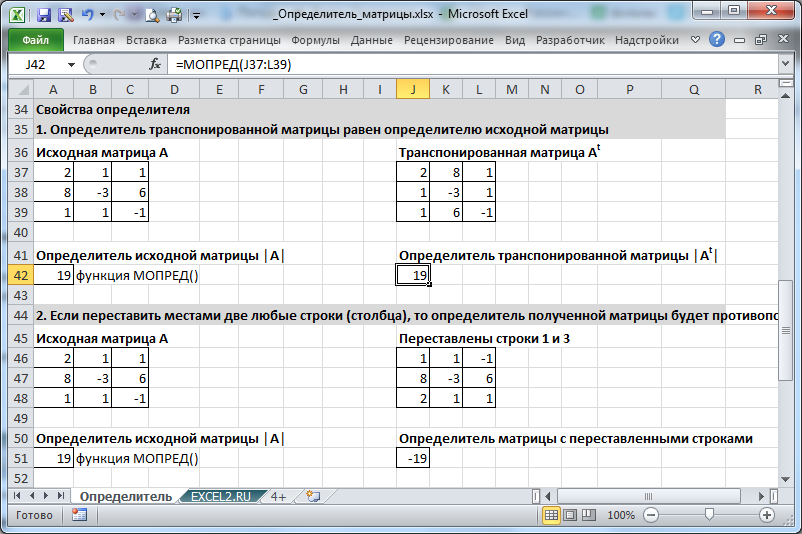
• Определитель транспонированной матрицы равен определителю исходной матрицы
• Если в матрице все элементы хотя бы одной из строк (или столбцов) нулевые, определитель такой матрицы равен нулю
• Если переставить местами две любые строки (столбца), то определитель полученной матрицы будет противоположен исходному (то есть, изменится знак)
• Если все элементы одной из строк (столбца) умножить на одно и тоже число k, то определитель полученной матрицы будет равен определителю исходной матрицы, умноженному на k
• Если матрица содержит строки (столбцы), являющиеся линейной комбинацией других строк (столбцов), то определитель =0
• det(А)=1/det(А ^-1 ), где А ^-1 - матрица обратная матрице А (А - квадратная невырожденная матрица).

Вычисление определителя матрицы по определению (до 6 порядка включительно)

СОВЕТ : Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОПРЕД() .

Как было показано выше для вычисления матриц порядка 2 и 3 существуют достаточно простые формулы и правила. Для вычисления определителя матриц более высокого порядка (без использования функции МОПРЕД() ) придется вспомнить определение:

Определителем квадратной матрицы порядка n х n является сумма, содержащая n! слагаемых ( =ФАКТР(n) ). Каждое слагаемое представляет собой произведение n элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А . Перед k-ым слагаемым появляется коэффициент (-1) , если элементы матрицы А в произведении упорядочены по номеру строки, а количество инверсий в k-ой перестановке множества номеров столбцов нечетно.

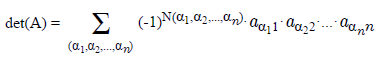
где ( α ₁ , α ₂ ,..., α _n ) - перестановка чисел от 1 до n , N( α ₁ , α ₂ ,..., α _n ) - число инверсий в перестановке , суммирование идёт по всем возможным перестановкам порядка n .

Попытаемся разобраться в этом непростом определении на примере матрицы 3х3.

Для матрицы 3 х 3, согласно определения, число слагаемых равно 3!=6, а каждое слагаемое состоит из произведения 3-х элементов матрицы. Ниже приведены все 6 слагаемых, необходимых для вычисления определителя матрицы 3х3:

• а21*а12*а33
• а21*а32*а13
• а11*а32*а23
• а11*а22*а33
• а31*а22*а13
• а31*а12*а23

а21, а12 и т.д. - это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.

Посмотрим на формулу выше (см. определение). Предположим, что второй индекс у каждого элемента матрицы (от 1 до n) соответствует номеру столбца матрицы (хотя это может быть номер строки (это не важно т.к. определители матрицы и ее транспонированной матрицы равны). Таким образом, второй индекс у первого элемента в произведении всегда равен 1, у второго - 2, у третьего 3. Тогда первые индексы у элементов соответствуют номеру строки и, в соответствии с определением, должны определяться из перестановок чисел от 1 до 3, т.е. из перестановок множества (1, 2, 3).

Теперь понятно, почему среди слагаемых нет а11*а22*а13, т.к. согласно определения ( в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А ), а в нашем слагаемом нет элемента из строки 3.

Примечание : Перестановкой из n чисел множества (без повторов) называется любое упорядочивание данного множества, отличающиеся друг от друга лишь порядком входящих в них элементов. Например, дано множество их 3-х чисел: 1, 2, 3. Из этих чисел можно составить 6 разных перестановок: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 1, 2), (3, 2, 1). См. статью Перестановки без повторений: Комбинаторика в MS EXCEL

Число перестановок множества из 3-х чисел =3!=6 (что, конечно, равно числу слагаемых в выражении для расчета определителя, т.к. каждому слагаемому соответствует своя перестановка). Для матрицы 3х3 все перестановки приведены в примечании выше. Можно убедиться, что в каждом слагаемом первые индексы у элементов равны соответствующим числам в перестановке. Например, для слагаемого а21*а12*а33 использована перестановка (2, 1, 3).

СОВЕТ : Для матрицы 4 порядка существует 4! перестановок, т.е. 26, что соответствует 26 слагаемым, каждое из которых является произведением различных 4-х элементов матрицы. Все 26 перестановок можно найти в статье Перебор всех возможных Перестановок в MS EXCEL .

Теперь, когда разобрались со слагаемыми, определим множитель перед каждым слагаемым (он может быть +1 или -1). Множитель определяется через четность числа инверсий соответствующей перестановки.

Примечание : Об инверсиях перестановок (и четности числа инверсий) можно почитать, например, в статье Перестановки без повторений: Комбинаторика в MS EXCEL

Например, первому слагаемому соответствует перестановка (2, 1, 3), у которой 1 инверсия (нечетное число) и, соответственно, -1 в степени 1 равно -1. Второму слагаемому соответствует перестановка (2, 3, 1), у которой 2 инверсии (четное число) и, соответственно, -1 в степени 2 равно 1 и т.д.

Сложив все слагаемые:  (-1)*(а21*а12*а33)+(+1)*(а21*а32*а13)+(-1)*(а11*а32*а23)+(+1)*(а11*а22*а33)+(-1)*(а31*а22*а13)+(+1)*(а31*а12*а23) получим значение определителя.

В файле примера на листе 4+, и зменяя порядок матрицы с помощью элемента управления Счетчик , можно вычислить определитель матрицы до 6 порядка включительно.

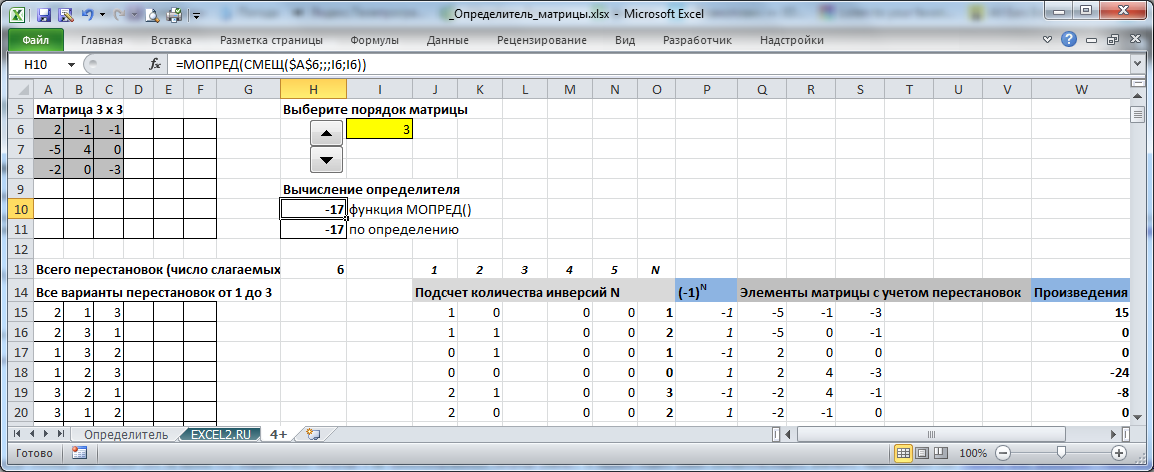
Следует учитывать, что при вычислении матрицы 6-го порядка в выражении используется уже 720 слагаемых (6!). Для 7-го порядка пришлось бы сделать таблицу для 5040 перестановок и, соответственно, вычислить 5040 слагаемых! Т.е. без использования МОПРЕД() не обойтись (ну, или можно вычислить определитель вручную методом Гаусса).