МНК: Приближение тригонометрическим полиномом в EXCEL
24 ноября 2018 г.
- Группы статей
- Статистический анализ
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью тригонометрического полинома.
В основной статье про МНК было рассмотрено приближение линейной функцией. В этой статье рассмотрим аппроксимацию методом наименьших квадратов с помощью тригонометрических многочленов (англ. Discrete Least Squares Approximation by Trigonometric Polynomials).
Под тригонометрическим многочленом будем понимать многочлен вида:
Максимальный порядок этого полинома k ограничен значением n/2, где n – это количество имеющихся пар значений (х i ; y i ), т.е. k<n/2.
Чтобы вычислить значение вышеуказанного полинома k-го порядка, для каждого заданного xi необходимо найти его коэффициенты a j и b j , включая a 0 и a k .
Напомним, что метод наименьших квадратов заключается в подборе таких коэффициентов полинома, при которых выражение
принимает минимальное значение.
Вышеуказанное выражение примет минимальное значение при таких коэффициентах, при которых соответствующие частные производные функции F равны нулю (аналогично тому, как мы делали для случая квадратичной зависимости ).
Сначала будем предполагать, что значения х i равномерно распределены на интервале [-π; п) или [0; 2п). А в конце статьи покажем, как избавиться от этого ограничения.
Сложный вывод коэффициентов приводить не будем, а запишем сразу конечный результат.
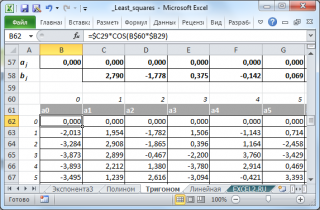
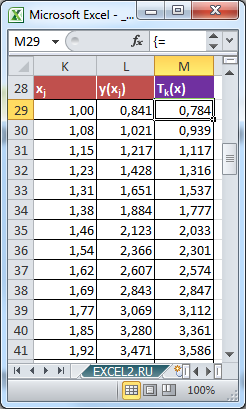
В файле примера на листе Триногом приведен расчет коэффициентов тригонометрического полинома T k (х), а затем и значения этого полинома для всех x i .
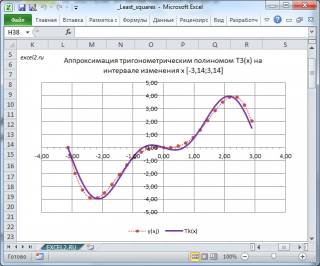
В качестве примера возьмем функцию y=x 2 *sin(x) на интервале [-п; п) и построим для нее аппроксимирующий тригонометрический полином третьего порядка T 3 (х).
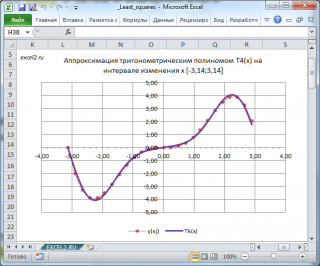
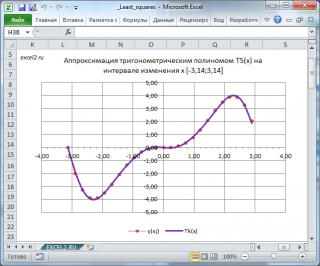
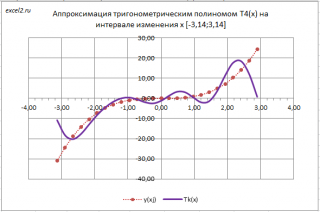
Покажем, что при увеличении порядка полинома k, точность аппроксимации увеличивается. Для этого построим T 4 (х) и T 5 (х).
Примечание : Т.к. период функции T k (х) равен 2п, то при аппроксимации функции f(x) (соответствующих значений этой функции), для которой f(-п)≠f(п), у нас могут быть проблемы с приближением. Например, сравните результаты приближения функции f(х)=x 2 , для которой f(-п) = f(п) и функции f(х)=x 3 , для которой f(-п)≠f(п). Оба приближения сделаны полиномом 4-го порядка T 4 (х).
Выходом из этой ситуации может стать выбор такого диапазона изменения х , для которого f(x 1 ) ≈ f(x n ). Но, часто это означает, что нам необходимо использовать интервал, отличный от [-п; п) или [0; 2п). Ниже покажем, как аппроксимировать функцию тригонометрическим полиномом на произвольном интервале.
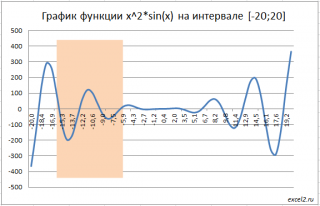
Возьмем ту же функцию y=x 2 *sin(x) на интервале (-20; 20). Предположим, что интервал аппроксимации равен (-15,8; 5,0) и выделим его цветом.
Границы интервала подобраны так, чтобы значения функции были примерно одинаковы в этих крайних точках.
Сначала вычислим значения аппроксимируемой функции y(x j ).
Напомним, что ранее для вычисления значений коэффициентов a j и b j мы использовали значения y(x j ) и значения x j из интервала [-п; п). Вроде бы, по аналогии, для мы должны поступить также: использовать y(x j ) и значения x j из интервала (-15,8; 5,0). Но, в этом случае мы не получим приемлемой точности аппроксимации.
Трюк заключается в следующем: для вычисления значений коэффициентов a j и b j мы будем по прежнему использовать значения y(x j ), а вместо значений x j из интервала (-15,8; 5,0) продолжим использовать x j из интервала [-п; п), но обозначим их как z j . Для расчета полинома T k также будем использовать значения z j .
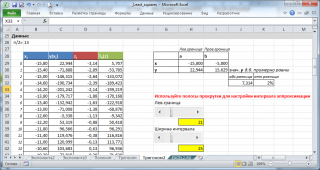
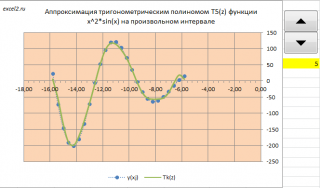
В файле примера на листе Триногом2 приведен расчет значений тригонометрического полинома T k (z). Там же построен график для визуального сравнения значений исходной функции y=x 2 *sin(x) и приближающего полинома.
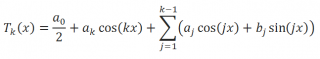
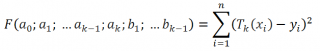
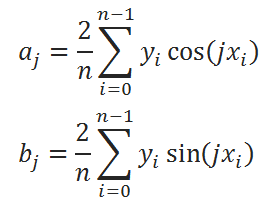
Комментарии