Изолинии в случае фигуры-плоскости в EXCEL

Пусть имеется функция двух переменных Z=f(X;Y). Изолинии (contour line) - это линии, в которой величина Z=const, т.е. изолинии соединяют точки, в которых функция сохраняет одинаковое значение. Часто изолинии используют для отображения 3D поверхностей второго порядка ( эллипсоид, эллиптический параболоид, гиперболический параболоид) на плоскости. В этой статье решим гораздо более скромную задачу: построим изолинии образуемые плоскостью в MS EXCEL . Изолинии в этом случае представляют собой прямые линии.

Обычно изолинии для функции двух переменных Z=f(X;Y) имеют достаточно сложную конфигурацию, т.к. соответствующая пространственная фигура сложна.

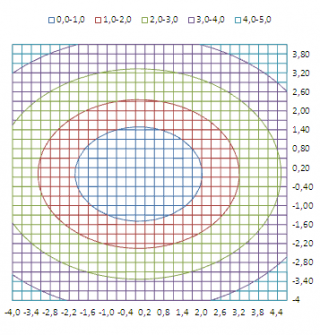
В статье Трехмерные диаграммы (поверхности и изолинии) в MS EXCEL показано как построить изолинии для поверхности задаваемой функцией  Z=-sin(X ² +Y ² )+1 с использованием штатных средств MS EXCEL (см. картинку ниже).

В этой статье рассмотрим построение изолиний для плоскости, которая наклонена к плоскости XY.

Плоскость задается уравнением A*X+B*Y+C*Z+D=0 или Z=d+a*Х+b*Y. Приравняв Z заданной постоянной величине (const), из предыдущего уравнения получим, что изолинии будут представлять собой прямые линии: Y=(const-d-a*Х)/b.

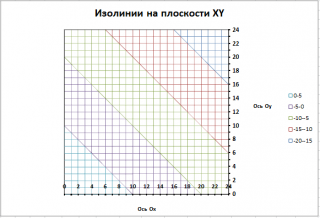
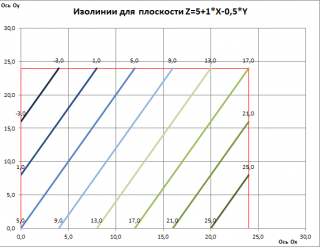
На картинке выше, изолинии построены на диаграмме типа Точечная .

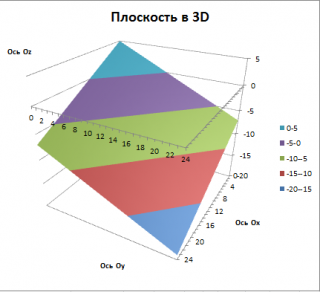
В файле примера приведены формулы для построения таких изолиний, а также диаграмма типа Поверхность, которая помогает представить расположение плоскости относительно плоскости XY.

В принципе изолинии можно построить и штатными средствами MS EXCEL, но в этом случае не удается контролировать количество отображаемых изолиний и их значения Z.

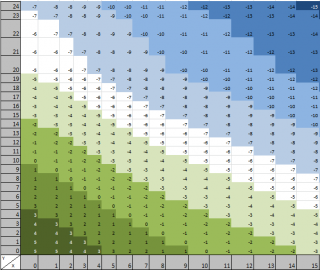
Для полноты картины упомянем еще один способ построения изолиний (ну, почти изолиний? точнее "изо-областей") - с помощью Условного форматирования .

Как видно на рисунке выше, значения ячеек с Z принадлежащих различным интервалам выделяются разными цветами. Это, наверное, простейший способ построения изолиний.

Построение изолиний на диаграмме типа Точечная

Но, вернемся к построению изолиний на диаграмме типа Точечная. В качестве исходных данных используем уравнение плоскости A*X+B*Y+C*Z+D=0 и диапазон изменения Х и Y.

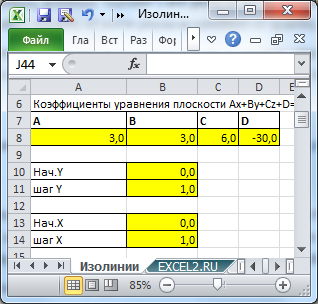
На диаграмме разместим 8 изолиний. Алгоритм построения изолиний следующий:

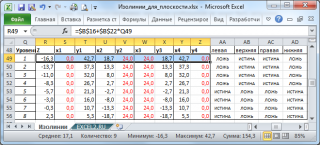
• Определяем диапазон изменения Z (ячейки В16:В18 );
• Определяем значения Z для каждой из 8-и изолинии (ячейки R 48:R56 );
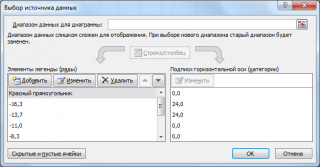
• Отображаем на диаграмме прямоугольник, соответствующий диапазонам изменения X и Y (красный прямоугольник), (ячейки Х 60:Y64 );
• Для каждого Z (т.е. для каждой изолинии) находим точки пересечения со сторонами прямоугольника (строки 49:56);
• Каждая изолиния пересекает какие-то 2 стороны прямоугольника, поэтому имеем 2 точки пересечения;
• Для каждой изолинии создаем на диаграмме отдельный ряд.

Названием ряда является соответствующее значение Z.

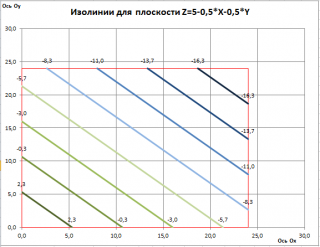
Покажем, как найти точку пересечения со сторонами красного прямоугольника. Для примера возьмем левую сторону. Нам известно: значение Z (=-16,3), уравнение плоскости (Z=5-0,5*Х-0,5*Y), значение X (для левой стороны Х равен минимальному значению, т.е. Х=0). Решая уравнение относительно Y получим значение 42,7 (см. ячейку Т49 ). Это значение больше максимального значения Y, поэтому делаем вывод, что изолиния с Z=-16,3 не пересекает левую сторону красного прямоугольника. Аналогично находятся точки пересечения изолинии с верхней, нижней и правой стороной (строка 49).

Если изолиния не пересекает сторону прямоугольника, то формула =И(T49<$Y$62;T49>$Y$61) вернет ЛОЖЬ, в противном случае - ИСТИНА. Т.к. изолиния пересекает только 2 стороны, то для каждой изолинии получим 2 значения ЛОЖЬ и 2 значения ИСТИНА. Для построения изолиний нам требуются только точки пересечения.

Формула массива

= НАИБОЛЬШИЙ((AA49:AD49=ИСТИНА)*(СТОЛБЕЦ(AA49:AD49))-СТОЛБЕЦ($AA$49)+1;{1;2})

определяет позиции точек пересечения.

Примечание : В вышеуказанной формуле массива использованы идеи из статьи Массив последовательных чисел в MS EXCEL .

И, наконец, формула =СМЕЩ($S49;;(AF49-1)*2) выводит значения Х и Y этих точек в отдельную таблицу ( Q59:V67 ) для построения рядов данных.

В итоге получим следующую диаграмму.

При изменении уравнения плоскости или диапазона изменения Х и Y, изолинии будут перестроены автоматически.