Доверительный интервал для оценки среднего (дисперсия известна) в EXCEL
27 ноября 2016 г.
- Группы статей
- Статистический вывод
Построим в MS EXCEL доверительный интервал для оценки среднего значения распределения в случае известного значения дисперсии.
В статье Статистики, выборочное распределение и точечные оценки в MS EXCEL дано определение точечной оценки параметра распределения (point estimator). Однако, в силу случайности выборки, точечная оценка не совпадает с оцениваемым параметром и более разумно было бы указывать интервал, в котором может находиться неизвестный параметр при наблюденной выборке х 1 , x 2 , ..., х n . Поэтому цель использования доверительных интервалов состоит в том, чтобы по возможности избавиться от неопределенности и сделать как можно более полезный статистический вывод .
Примечание : Процесс обобщения данных выборки , который приводит к вероятностным утверждениям обо всей генеральной совокупности , называют статистическим выводом (statistical inference).
СОВЕТ : Для построения Доверительного интервала нам потребуется знание следующих понятий:
- дисперсия и стандартное отклонение ,
- выборочное распределение статистики ,
- уровень доверия/ уровень значимости ,
- стандартное нормальное распределение и его квантили .
К сожалению, интервал, в котором может находиться неизвестный параметр, совпадает со всей возможной областью изменения этого параметра, поскольку соответствующую выборку , а значит и оценку параметра , можно получить с ненулевой вероятностью. Поэтому приходится ограничиваться нахождением границ изменения неизвестного параметра с некоторой заданной наперед вероятностью.
Определение : Доверительным интервалом называют такой интервал изменения случайной величины , которыйс заданной вероятностью , накроет истинное значение оцениваемого параметра распределения.
Эту заданную вероятность называют уровнем доверия (или доверительной вероятностью ).
Обычно используют значения уровня доверия 90%; 95%; 99%, реже 99,9% и т.д. Например, уровень доверия 95% означает, что дополнительное событие, вероятность которого 1-0,95=5%, исследователь считает маловероятным или невозможным.
Примечание : Вероятность этого дополнительного события называется уровень значимости или ошибка первого рода . Подробнее см. статью Уровень значимости и уровень надежности в MS EXCEL .
Разумеется, выбор уровня доверия полностью зависит от решаемой задачи. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.
Примечание : Построение доверительного интервала в случае, когда стандартное отклонение неизвестно, приведено в статье Доверительный интервал для оценки среднего (дисперсия неизвестна) в MS EXCEL . О построении других доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .
Формулировка задачи
Предположим, что из генеральной совокупности имеющей нормальное распределение взята выборка размера n. Предполагается, что стандартное отклонение этого распределения известно. Необходимо на основании этой выборки оценить неизвестное среднее значение распределения (μ, математическое ожидание ) и построить соответствующий двухсторонний доверительный интервал .
Точечная оценка
Как известно из
Центральной предельной теоремы
,
статистика
![]() (обозначим ее
Х
ср
) является
несмещенной оценкой среднего
этой
генеральной совокупности
и имеет распределение N(μ;σ
2
/n).
(обозначим ее
Х
ср
) является
несмещенной оценкой среднего
этой
генеральной совокупности
и имеет распределение N(μ;σ
2
/n).
Примечание : Что делать, если требуется построить доверительный интервал в случае распределения, которое не является нормальным? В этом случае на помощь приходит Центральная предельная теорема , которая гласит, что при достаточно большом размере выборки n из распределения не являющемся нормальным , выборочное распределение статистики Х ср будет приблизительно соответствовать нормальному распределению с параметрами N(μ;σ 2 /n).
Итак, точечная оценка среднего значения распределения у нас есть – это среднее значение выборки , т.е. Х ср . Теперь займемся доверительным интервалом.
Построение доверительного интервала
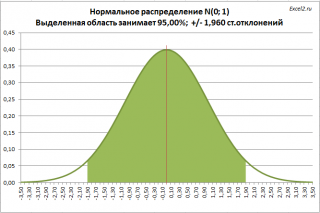
Обычно, зная распределение и его параметры, мы можем вычислить вероятность того, что случайная величина примет значение из заданного нами интервала. Сейчас поступим наоборот: найдем интервал, в который случайная величина попадет с заданной вероятностью. Например, из свойств нормального распределения известно, что с вероятностью 95%, случайная величина, распределенная по нормальному закону , попадет в интервал примерно +/- 2 стандартных отклонения от среднего значения (см. статью про нормальное распределение ). Этот интервал, послужит нам прототипом для доверительного интервала .
Теперь разберемся,знаем ли мы распределение , чтобы вычислить этот интервал? Для ответа на вопрос мы должны указать форму распределения и его параметры.
Форму распределения мы знаем – это нормальное распределение (напомним, что речь идет о выборочном распределении статистики Х ср ).
Параметр μ нам неизвестен (его как раз нужно оценить с помощью доверительного интервала ), но у нас есть его оценка Х ср , вычисленная на основе выборки, которую можно использовать.
Второй параметр – стандартное отклонение выборочного среднего будем считать известным , он равен σ/√n.
Т.к. мы не знаем μ, то будем строить интервал +/- 2 стандартных отклонения не от среднего значения , а от известной его оценки Х ср . Т.е. при расчете доверительного интервала мы НЕ будем считать, что Х ср попадет в интервал +/- 2 стандартных отклонения от μ с вероятностью 95%, а будем считать, что интервал +/- 2 стандартных отклонения от Х ср с вероятностью 95% накроет μ – среднее генеральной совокупности, из которого взята выборка . Эти два утверждения эквивалентны, но второе утверждение нам позволяет построить доверительный интервал .
Кроме того, уточним интервал: случайная величина, распределенная по нормальному закону , с вероятностью 95% попадает в интервал +/- 1,960 стандартных отклонений, а не+/- 2 стандартных отклонения . Это можно рассчитать с помощью формулы =НОРМ.СТ.ОБР((1+0,95)/2) , см. файл примера Лист Интервал .
Теперь мы можем сформулировать вероятностное утверждение, которое послужит нам для формирования доверительного интервала : «Вероятность того, что среднее генеральной совокупности находится от среднего выборки в пределах 1,960 « стандартных отклонений выборочного среднего» , равна 95%».
Значение вероятности, упомянутое в утверждении, имеет специальное название уровень доверия , который связан с уровнем значимости α (альфа) простым выражением уровень доверия = 1 -α . В нашем случае уровень значимости α =1-0,95=0,05 .
Теперь на основе этого вероятностного утверждения запишем выражение для вычисления доверительного интервала :
где Z α/2 – верхний α/2-квантиль стандартного нормального распределения (такое значение случайной величины z , что P ( z >= Z α/2 )=α/2 ).
Примечание : Верхний α/2-квантиль определяет ширину доверительного интервала в стандартных отклонениях выборочного среднего. Верхний α/2-квантиль стандартного нормального распределения всегда больше 0, что очень удобно.
В нашем случае при α=0,05, верхний α/2-квантиль равен 1,960. Для других уровней значимости α (10%; 1%) верхний α/2-квантиль Z α/2 можно вычислить с помощью формулы =НОРМ.СТ.ОБР(1-α/2) или, если известен уровень доверия , =НОРМ.СТ.ОБР((1+ур.доверия)/2) .
Обычно при построении доверительных интервалов для оценки среднего используют только верхний α /2- квантиль и не используют нижний α /2- квантиль . Это возможно потому, что стандартное нормальное распределение симметрично относительно оси х ( плотность его распределения симметрична относительно среднего, т.е. 0 ) . Поэтому, нет нужды вычислять нижний α/2-квантиль (его называют просто α /2-квантиль ), т.к. он равен верхнему α /2- квантилю со знаком минус.
Напомним, что, не смотря на форму распределения величины х, соответствующая случайная величина Х ср распределена приблизительно нормально N(μ;σ 2 /n) (см. статью про ЦПТ ). Следовательно, в общем случае, вышеуказанное выражение для доверительного интервала является лишь приближенным. Если величина х распределена по нормальному закону N(μ;σ 2 /n), то выражение для доверительного интервала является точным.
Расчет доверительного интервала в MS EXCEL
Решим задачу. Время отклика электронного компонента на входной сигнал является важной характеристикой устройства. Инженер хочет построить доверительный интервал для среднего времени отклика при уровне доверия 95%. Из предыдущего опыта инженер знает, что стандартное отклонение время отклика составляет 8 мсек. Известно, что для оценки времени отклика инженер сделал 25 измерений, среднее значение составило 78 мсек.
Решение : Инженер хочет знать время отклика электронного устройства, но он понимает, что время отклика является не фиксированной, а случайной величиной, которая имеет свое распределение. Так что, лучшее, на что он может рассчитывать, это определить параметры и форму этого распределения.
К сожалению, из условия задачи форма распределения времени отклика нам не известна (оно не обязательно должно быть нормальным ). Среднее, т.е. математическое ожидание , этого распределения также неизвестно. Известно только его стандартное отклонение σ=8. Поэтому, пока мы не можем посчитать вероятности и построить доверительный интервал .
Однако, не смотря на то, что мы не знаем распределение времени отдельного отклика , мы знаем, что согласно ЦПТ , выборочное распределение среднего времени отклика является приблизительно нормальным (будем считать, что условия ЦПТ выполняются, т.к. размер выборки достаточно велик (n=25)) .
Более того, среднее этого распределения равно среднему значению распределения единичного отклика, т.е. μ. А стандартное отклонение этого распределения (σ/√n) можно вычислить по формуле =8/КОРЕНЬ(25) .
Также известно, что инженером была получена точечная оценка параметра μ равная 78 мсек (Х ср ). Поэтому, теперь мы можем вычислять вероятности, т.к. нам известна форма распределения ( нормальное ) и его параметры (Х ср и σ/√n).
Инженер хочет знать математическое ожидание μ распределения времени отклика. Как было сказано выше, это μ равно математическому ожиданию выборочного распределения среднего времени отклика . Если мы воспользуемся нормальным распределением N(Х ср ; σ/√n), то искомое μ будет находиться в интервале +/-2*σ/√n с вероятностью примерно 95%.
Уровень значимости равен 1-0,95=0,05.
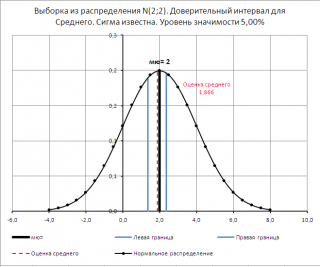
Наконец, найдем левую и правую границу доверительного интервала . Левая граница: =78-НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25) = 74,864 Правая граница: =78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136
или так
Левая граница: =НОРМ.ОБР(0,05/2; 78; 8/КОРЕНЬ(25)) Правая граница: =НОРМ.ОБР(1-0,05/2; 78; 8/КОРЕНЬ(25))
Ответ : доверительный интервал при уровне доверия 95% и σ =8 мсек равен 78+/-3,136 мсек.
В файле примера на листе Сигма известна создана форма для расчета и построения двухстороннего доверительного интервала для произвольных выборок с заданным σ и уровнем значимости .
Функция ДОВЕРИТ.НОРМ()
Если значения выборки находятся в диапазоне B20:B79 , а уровень значимости равен 0,05; то формула MS EXCEL: =СРЗНАЧ(B20:B79)-ДОВЕРИТ.НОРМ(0,05;σ; СЧЁТ(B20:B79)) вернет левую границу доверительного интервала .
Эту же границу можно вычислить с помощью формулы: =СРЗНАЧ(B20:B79)-НОРМ.СТ.ОБР(1-0,05/2)*σ/КОРЕНЬ(СЧЁТ(B20:B79))
Примечание : Функция ДОВЕРИТ.НОРМ() появилась в MS EXCEL 2010. В более ранних версиях MS EXCEL использовалась функция ДОВЕРИТ() .
Комментарии