Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в EXCEL

Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.

Решим систему из 3-х линейных алгебраических уравнений с помощью обратной матрицы (матричным методом).

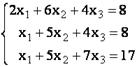
СОВЕТ : Решение СЛАУ методом Крамера приведено в статье Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL .

Запишем в ячейки основную матрицу системы и столбец свободных членов.

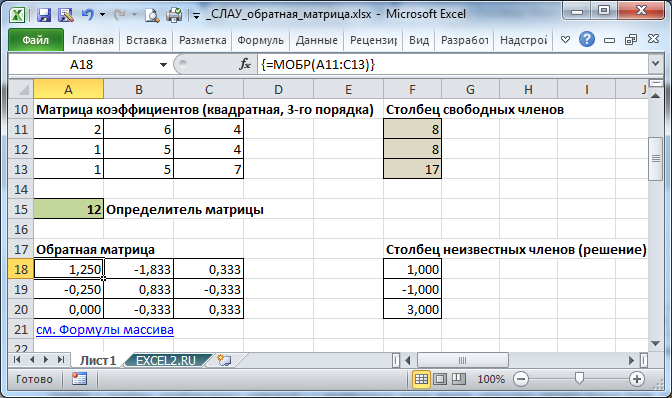
Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основной матрицы системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.

Вычислим обратную матрицу с помощью формулы массива МОБР() .

Для этого выделите ячейки A18:C20 , а в Строке формул введите =МОБР(A11:C13) , затем нажмите CTRL+SHIFT+ENTER .

Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов. Перемножить матрицы можно с помощью формулы массива =МУМНОЖ() .

Для этого выделите ячейки F18:F20 , а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13) , затем нажмите CTRL+SHIFT+ENTER .

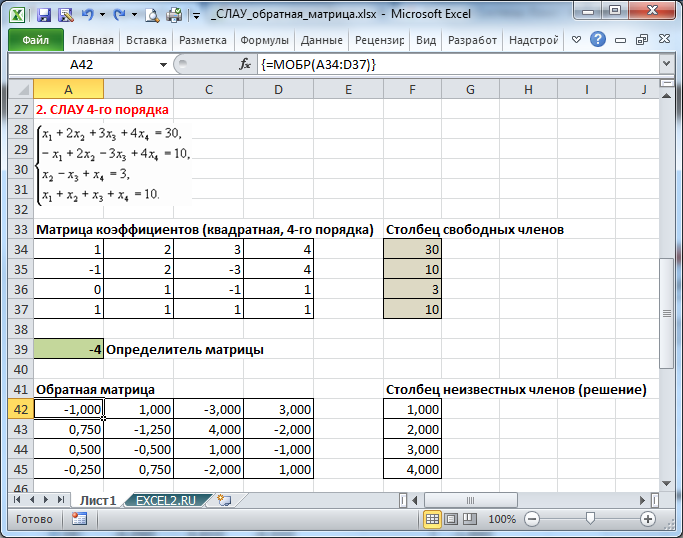
В файле примера также приведено решение системы 4-х и 5-и уравнений.