Поиск решения EXCEL (6.3). Задача коммивояжера (полный граф, линейная модель)
27 марта 2015 г.
- Группы статей
- Надстройка "Поиск решения"
Решим один из вариантов задачи коммивояжера для небольшого количества городов (5-10) с помощью надстройки Поиск решения. Построим линейную модель.
Рассмотрим задачу коммивояжера (англ. Travelling Salesman Problem, TSP) заключающуюся в отыскании самого короткого маршрута, проходящего через заданные города по одному разу с последующим возвратом в исходный город (также рассмотрим вариант без возврата). Подобная задача решена в статье Поиск решения MS EXCEL (6.2). Задача коммивояжера (полный граф, нелинейная модель) с помощью нелинейной модели.
Задача
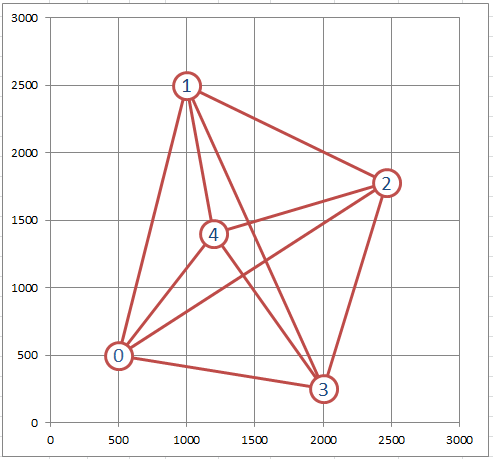
Найдем кратчайший путь между 5 городами, координаты которых известны. Сначала рассмотрим замкнутый вариант задачи: коммивояжёру требуется посетить все города, после чего вернуться в исходный город.
Создание модели
Так как даны координаты городов, то сначала найдем расстояния между ними (см. файл примера, лист 5 городов ).
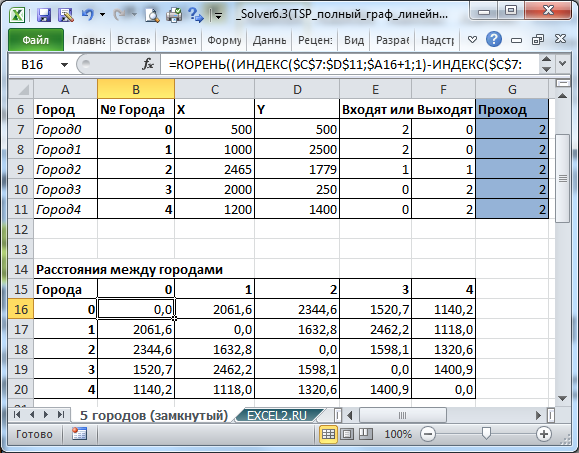
Расстояния рассчитаем с помощью формулы: = КОРЕНЬ((ИНДЕКС($C$7:$D$11;$A16+1;1)-ИНДЕКС($C$7:$D$11;B$15+1;1))^2+(ИНДЕКС($C$7:$D$11;$A16+1;2)-ИНДЕКС($C$7:$D$11;B$15+1;2))^2)
Теперь создадим модель для Поиска решения .
Совет : Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Переменные (выделено зеленым) . В качестве переменных модели следует взять номера всех маршрутов соединяющих города. Маршрут из города 0 в город 1 эквивалентен маршруту из 1 в 0, так как направление обхода городов не имеет значения. Необходимо соединить все города (полный граф).
Ограничения (выделено синим) . Необходимо, чтобы из каждого города был 1 входящий и 1 исходящий маршрут.
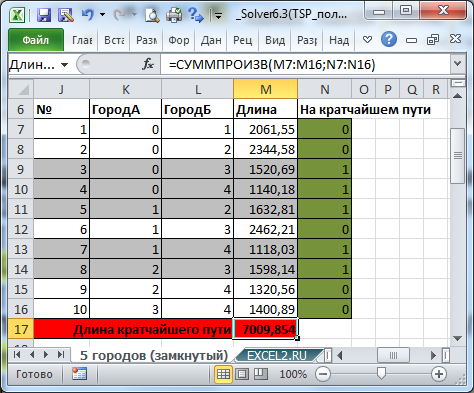
Целевая функция (выделено красным) . Длина маршрута должна быть минимальной.
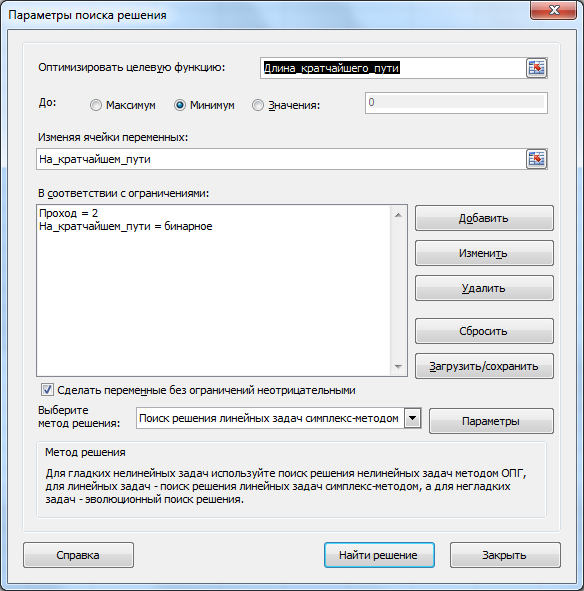
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .
Найденное Решение
Поиск решения гарантировано найдет самый короткий маршрут, т.к. построенная нами модель линейная.
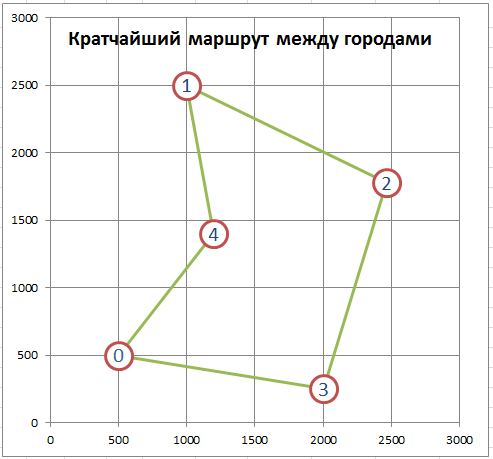
Данную задачу можно решить для максимального количества городов =20, т.к. число маршрутов (ребер) вычисляется по формуле n*(n-1)/2, а количество переменных у Поиска решения ограничено 200.
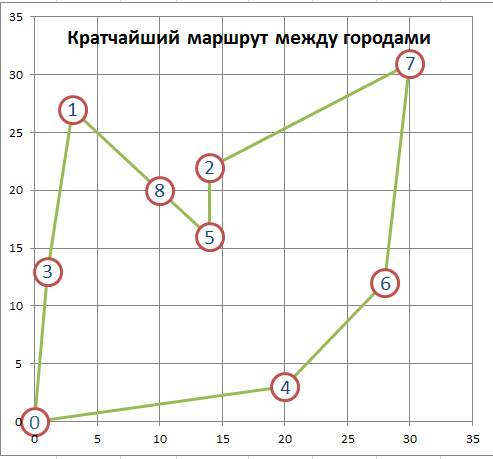
Также в файле примера приведено решение задачи для прохождения 5 городов по незамкнутому маршруту, а также задачу для 9 городов.
Совет : Решение задачи о поиске кратчайшего пути между 2-мя заданными городами можно найти в статье Поиск решения MS EXCEL (6.4). Кратчайший путь (неполный граф, линейная модель) .
Комментарии