Поиск решения EXCEL (6.1). Задача линейного программирования (ЛП)
27 марта 2015 г.
- Группы статей
- Надстройка "Поиск решения"
Решим задачу линейного программирования с помощью надстройки Поиск решения.
В этой статье мы отойдем от формулировки практических задач и решим задачу линейного программирования в абстрактных терминах: вектор переменных х, матрица ограничений A х , вектор b , целевая функция cTx (вместо более привычных: объем производства, количество комплектующих разного вида, максимальный доход). Задача линейного программирования (ЛП) есть задача максимизации линейной функции при линейных ограничениях. Задачу ЛП можно записать несколькими стандартными способами. Мы сформулируем ее в форме max { cTx : Ax < b , x >0}
Задача
Необходимо максимизировать целевую функцию cTx: max 50* x1 + 30* x2 + 25* x3 + 30* x4 при условии, что: 2* x1 + 2,5* x2 + 3* x3 + 1,8* x4 <= 800 1,2* x1 + x2 + 2* x3 + 0,8* x4 <= 400 1,5* x1 + 1,2* x2 + 1,5* x3 + 0,8* x4 <=380 x2 >= 50 x3 >= 30 x1; x2; x3; x4 >= 0
cTx - это векторное произведение векторов cT (транспонированный вектор с) и х.
Примечание : эта задача эквивалентна задаче определения оптимальной структуры производства с целью максимизации дохода (см. статью Поиск решения MS EXCEL (1.1). Оптимальная структура выпускаемой продукции ). Сформулируем эту задачу в общем виде: Предприятие планирует производить n видов продукции, используя m видов ресурсов. Для производства единицы j-го продукта требуется aij единиц i-го ресурса. Стоимость единицы j-го продукта равна cj. В наличии имеется bi единиц i-го ресурса. Нужно определить план производства с целью максимизировать прибыль. Обозначив хj - объем выпуска продукции j-го вида (j =1;…;n), мы можем записать задачу поиска оптимального производственного плана следующим образом:
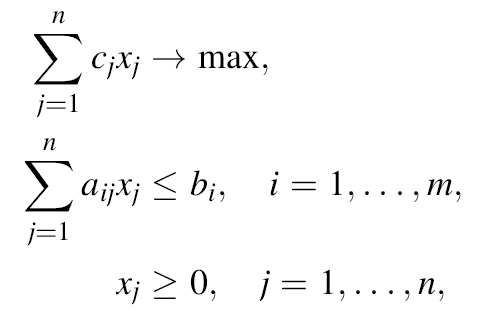
Или в матричной форме:

Получается, что в исходной задаче:
- вектор с (стоимость продукции) равен (50; 30; 25; 30)
- вектор x (количество продукции) необходимо найти для заданных условий
- n=4 (4 вида продукции)
- m=3 (3 вида ресурсов)
- вектор b (количество ресурсов) равен (800; 400; 380)
- матрица A (количество единиц ресурсов для изготовления продукта) равна (2; 2,5; 3; 1,8 : 1,2; 1; 2; 0,8 : 1,5; 1,2; 1,5; 0,8)
Теперь создадим модель.
Создание модели
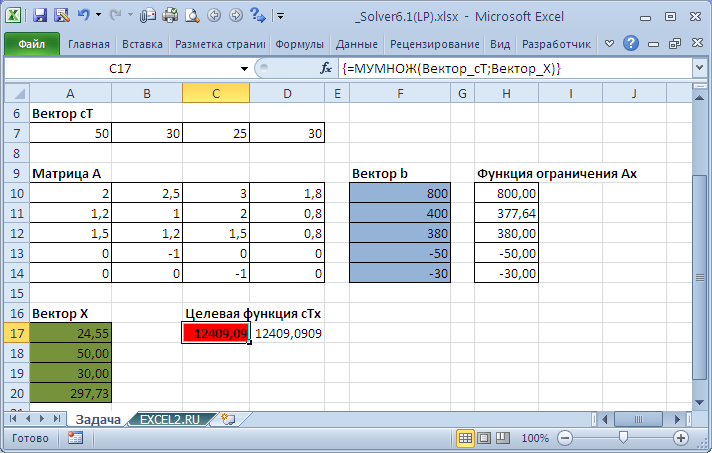
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).
Для решения задачи на листе MS EXCEL необходимо записать матрицу А , вектора b и cT (предварительно все неравенства переведены в форму меньше или равно путем умножения соответствующих уравнений на -1):
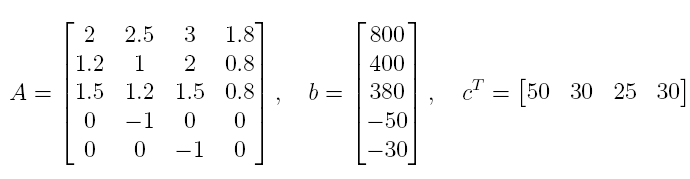
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .
Совет : Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Значение целевой функции cTx получено путем матричного умножения векторов cT и x (используйте функцию МУМНОЖ() , которая вводится как формула массива ). Аналогично получена функция ограничений Ах , путем умножения матрицы А на х . Так как матрица Ах имеет размерность 5х1, то перед вводом формулы = МУМНОЖ(Матрица_А;Вектор_Х) необходимо выделить столбец из 5 ячеек, затем после записи формулы в Строке формул , нажмите CTRL + SHIFT + ENTER для ее ввода.
Настроить Поиск решения нужно следующим образом:
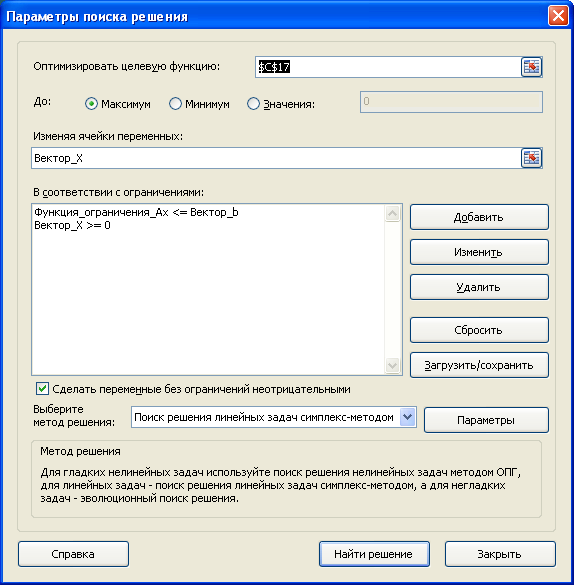
Комментарии