Аннуитет. Определяем в EXCEL Приведенную (Текущую) стоимость

Определим Приведенную (текущую) стоимость будущих доходов (или расходов) в случае аннуитета. Для этого будем использовать функцию ПС() . Также выведем альтернативную формулу для расчета Текущей стоимости.

Текущая стоимость (Present Value) рассчитывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Расчет Текущей стоимости, также как и Будущей стоимости важен, так как, платежи, осуществленные в различные моменты времени, можно сравнивать лишь после приведения их к одному временному моменту. Текущая стоимость зависит от того, каким методом начисляются проценты: простые проценты , сложные проценты или аннуитет . Текущая стоимость получается как результат приведения будущих доходов (или расходов) к начальному периоду времени. Например, сумма 100 000р. на расчетном счету через 5 лет эквивалентна сегодняшней сумме 62092,13р. при действующей процентной ставке 10% (начисление % ежегодное; пополнения нет). Результат получен по формуле =ПС(10%;5;0;-100000) . Проверить результат можно по этой формуле =БС(10%;5;0;-62092,13) .

Примечание : Если денежные потоки представлены в виде платежей произвольной величины, осуществляемые через равные промежутки времени, то для нахождения Текущей стоимости по методу сложных процентов используется функция ЧПС() . Если денежные потоки представлены в виде платежей произвольной величины, осуществляемых за любые промежутки времени, то используется функция ЧИСТНЗ() .

В MS EXCEL Текущая стоимость для аннуитета и для сложных процентов по постоянной процентной ставке через одинаковые промежутки времени рассчитывается функцией ПС() .

Синтаксис ПС()

Функция ПС(ставка; кпер; плт; [бс]; [тип]) позволяет определить сумму кредита, на которую можно рассчитывать, зная сумму ежемесячного платежа, срок кредита и процентную ставку. Функцию ПС() можно использовать также если требуется определить начальную сумму вклада, которую нужно положить на счет, чтобы через определенное количество лет получить желаемую сумму (ставка и период капитализации процентов известен).

Аргументы функции: Ставка (rate, interest). Процентная ставка за период , чаще всего за год или за месяц. Обычно задается через годовую ставку, деленную на количество периодов в году. При годовой ставке 10% месячная ставка составит 10%/12. Ставка не изменяется в течение всего срока аннуитета. Кпер (nper). Общее число периодов платежей по аннуитету . Если кредит взят на 5 лет, а выплаты производятся ежемесячно, то всего 60 периодов (12 мес. в году*5 лет) ПЛТ (pmt, payment). Регулярный платеж, осуществляемый каждый период . Платеж – постоянная величина, она не меняется в течение всего срока аннуитета. Бс (fv, future value). Будущая стоимость в конце срока аннуитета (по истечении числа периодов Кпер). Бс - требуемое значение будущей стоимости или остатка средств после последней выплаты. Например, в случае расчета аннуитетного платежа для полной выплаты ссуды к концу срока Бс = 0, т.к. ссуда в конце срока должна быть полностью погашена. Тип (type). Число 0 или 1, обозначающее, когда должна производиться выплата (и соответственно начисление процентов). 0 – в конце периода, 1 – в начале. Подробнее о постнумерандо и пренумерандо см. в разделе Немного теории в статье об аннуитете .

Примечание . Английский вариант функции: PV(rate, nper, pmt, [fv], [type]), т.е. Present Value – будущая стоимость.

Расчеты в ПС() производятся по этой формуле:

Использование функции ПС() в случае выплаты кредита

Определим сумму кредита, на которую можно рассчитывать, зная сумму ежемесячного платежа, срок кредита и процентную ставку (см. файл примера Лист Кредит ).

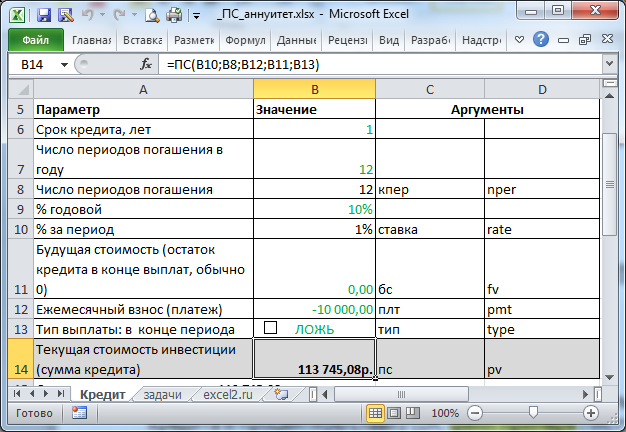
Пусть ежемесячный взнос =10000р. (плт), ставка по кредиту 10% (ставка). Кредит планируется вернуть в течение года (кпер=12). Взнос в конце месяца (тип=0). Записав формулу =ПС(10%/12; 12; -10000; 0; 0) получим ответ 113 745,08р., т.е. взяв эту сумму в кредит и выплачивая по 10000р. ежемесячно, мы погасим полностью кредит через 12 месяцев.

Пример вычисления остатка суммы основного долга (при БС=0, тип=0)

Пусть был взят кредит в размере 100 000руб. на 10 лет под ставку 9%. Кредит должен гаситься ежемесячными равными платежами (в конце периода). Требуется вычислить сумму основного долга, которая будет выплачена в первом месяце третьего года выплат. Решение простое – используйте функцию ОСПЛТ(): =ОСПЛТ(9%/12;25;10*12;100000) Ставка за период (ставка): 9%/12 Номер периода (первый месяц третьего года выплат): 25=2*12+1 Всего периодов (кпер): 10*12 Кредит: 100000 Сумма основного долга, которая будет выплачена в первом месяце третьего года выплат: -618,26руб.

Теперь выполним те же вычисления, только осмысленно, т.е. понимая, суть расчета.

1. Вычислим ежемесячный платеж, используя формулу приведенной стоимости. Обозначим сумму кредита как ПС, ежемесячный платеж как ПЛТ: ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Отсюда, ПМТ=ПС* ставка /(1-(1+ставка)^-кпер)=1266,76 (правильность расчета можно проверить с помощью ПЛТ() – см. статью Аннуитет. Расчёт в MS EXCEL погашение основной суммы долга ). ПЛТ() вернет -1266,76. Знак минус указывает на различные направления денежных потоков + (из банка сумма кредита), - (в банк ежемесячные платежи). Формула приведенной стоимости является следствием того, что сумма долей ежемесячных платежей, идущих на погашение основной суммы долга, должна быть равна сумме кредита. Поясним:
1. Доля платежа, которая идет на погашение основной суммы долга в 1-й период =ПМТ-ПС*ставка, а с учетом знаков =-ПМТ-ПС*ставка (чтобы сумма долей была того же знака, что и ПС). Обозначим эту долю как ПС1. Кстати, ПС*ставка – это сумма процентов, уплаченная за пользование кредитом в первый период.
2. Доля платежа, которая идет на погашение основной суммы долга в 2-й период =-ПМТ-(ПС-ПС1)*ставка=-ПМТ-(ПС +ПМТ+ПС*ставка) *ставка=(-ПМТ-ПС*ставка)*(1+ставка)=ПС1*(1+ставка). Обозначим эту долю как ПС2. Кстати, ПС-ПС1 – это остаток суммы долга в конце второго периода.
3. Доля платежа, которая идет на погашение основной суммы долга в 3-й период =-ПМТ-(ПС-ПС1-ПС2)*ставка=-ПМТ-(ПС-ПС1)*ставка+ПС2*ставка =ПС2+ПС2*ставка= ПС2*(1+ставка) =ПС1*(1+ставка)^2
4. Очевидно, что доля платежа, которая идет на погашение основной суммы долга в последний период (кпер)= ПС1*(1+ставка)^ кпер =-(ПМТ+ПС*ставка) *(1+ставка)^ кпер
5. Чтобы погасить кредит полностью, необходимо, чтобы сумма долей, идущих на погашение кредита, была равна сумме кредита, т.е. =-(ПМТ+ПС*ставка)*(1-(1+ставка)^ кпер)/ставка=ПС. Эта формула получена как сумма членов геометрической прогрессии: первый член =-(ПМТ+ПС*ставка), знаменатель =(1+ставка).
6. Решая нехитрое уравнение, полученное на предыдущем шаге, получим, что ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Это и есть формула приведенной стоимости (при БС=0 и платежах, осуществляемых в конце периода (тип=0)).
2. Вычислим сумму основного долга, которую нужно будет выплатить начиная с 25-го месяца (т.е. в начиная с 25 и заканчивая 120 периодом). Сделаем это так же используя формулу приведенной стоимости ПС=ПМТ*(1-(1+ставка)^-кпер)/ставка. Теперь ПМТ нам известно, ПС – это искомая сумма основного долга, которую нужно будет выплатить, начиная с 25-го месяца, т.е. за 96 периодов (120-24=кпер). ПС=86466,91 Правильность расчета можно проверить с помощью ОБЩДОХОД() .
3. Вычислим сумму процентов, которые будут выплачены в 25-й месяц: 86466,91*ставка=648,50 Правильность расчета можно проверить с помощью ПРПЛТ() .
4. Наконец, т.к. каждый платеж содержит сумму, идущую в оплату основной суммы долга и начисленные за период проценты, то Сумму основного долга, которая будет выплачена в первом месяце третьего года выплат получим как: ПМТ-648,50=618,26

Как видим, сумма совпадает результатом ОСПЛТ() , вычисленную ранее (с точностью до знака).

Примечание : в файле примера приведено решение нескольких простых задач по определению Текущей стоимости .