Как показано в соответствующих статьях на нашем сайте excel2.ru, исходный ряд можно сгладить разными методами:

•     скользящее среднее;
•     взвешенное скользящее среднее и его модификации (центрированное скользящее среднее и взвешенное центрированное скользящее среднее);
•     экспоненциальное сглаживание

Какой из методов лучше сглаживает исходный ряд? Как правило, для ответа на этот вопрос вычисляются ошибки (разности) между соответствующими точками рядов (исходного и скользящего среднего), т.е. e_i=y_i-ŷ_i. Интуитивно понятно, что лучше тот метод сглаживания, суммарная ошибка которого меньше.

Виды ошибок

Суммарную ошибку можно найти несколькими способами:

Средняя абсолютная ошибка (англ. Mean Absolute Error, MAE)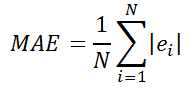 

Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)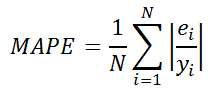

Среднеквадратичная ошибка (англ. Root Mean Squared Error, RMSE)

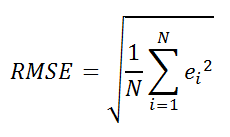
В наших вычислениях будем использовать RMSE. Для вычисления этой ошибки в EXCEL используется следующий алгоритм:

•     вычисляются ошибки (разности) между соответствующими точками рядов (исходного и скользящего среднего), т.е. e_i=y_i-ŷ_i;
•     вычисляются квадраты этих ошибок (Errors Squared);
•     затем находят сумму этих квадратов ошибок - SSE (Sum of the Squared Errors);
•     разделив SSE на количество точек ряда скользящего среднего, получим ошибку, которая в англоязычной литературе называется MSE (Mean Squared Error). SSE имеет размерность дисперсии. Математически можно показать, что SSE равна дисперсии ошибок плюс квадрат средней ошибки (дисперсия вычисляется как для генеральной совокупности, а не как для выборки);

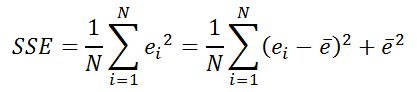
•     И, наконец, Среднеквадратичная ошибка (RMSE) вычисляется путем извлечения квадратного корня из MSE.

Примечание: Формула для расчета Среднеквадратичной ошибки (RMSE) практически совпадает с формулой для стандартной ошибки регрессии (Standard Error of the Regression). Отличие состоит в том, что стандартная ошибка регрессии учитывает поправку на количество оцениваемых параметров (сумма квадратов ошибок делится не на n, а на n-p, где p – количество оцениваемых параметров модели). Т.к. количество параметров обычно невелико (1, 2 или 3), то при больших n различие этих значений ошибок незначительно.

Для удобства сравнения методов сглаживания в файле примера создана соответствующая форма.

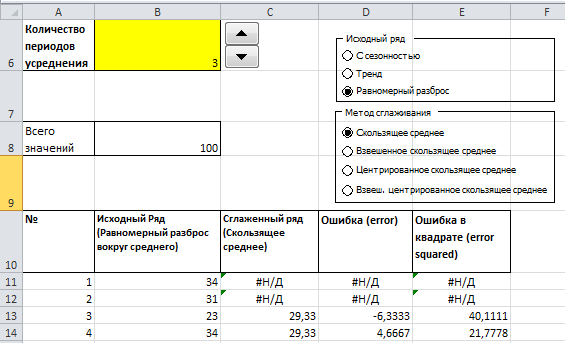
С помощью Переключателей в форме можно выбрать тип исходного ряда (С сезонностью, Растущий тренд или Равномерный разброс). Также можно выбрать один из 5 методов сглаживания и количество периодов сглаживания.

В зависимости от выбранных опций будет автоматически выведена диаграмма с исходным рядом и сглаженной кривой.

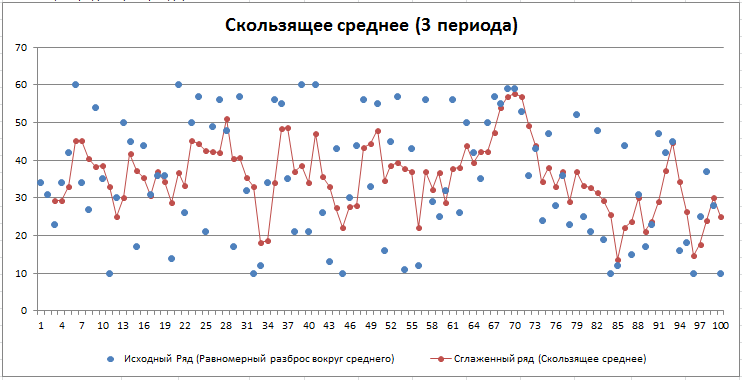
Также будет вычислена среднеквадратичная ошибка RMSE (ячейка K9 в файле примера).

Если метод сглаживания «уловил» тренд исходного ряда, то
1) распределение ошибок (или остатки, англ. residuals) должно быть приблизительно нормальным со средним значением близким к 0. 

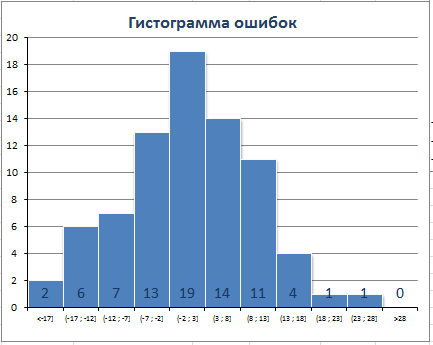
Примечание: В случае, если исходный ряд представляет собой случайный равномерный разброс вокруг некоторого среднего (в MS EXCEL это можно реализовать с помощью функции СЛУЧМЕЖДУ()), то очевидно, что распределение ошибок не будет нормальным. Используя форму EXCEL для генерации трендов можно убедиться в этом непосредственно.

2) Разброс ошибок не должен меняться в зависимости от периода.

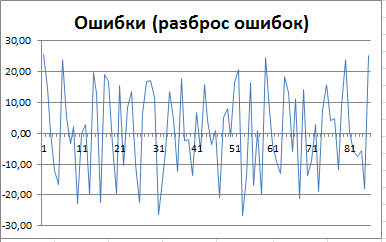
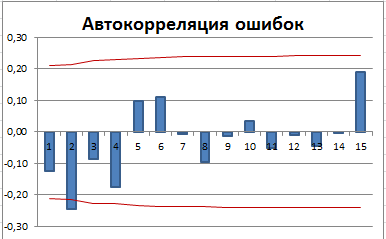
3) Должна отсутствовать автокорреляция ошибок (ошибки должны быть независимыми случайными величинами). 

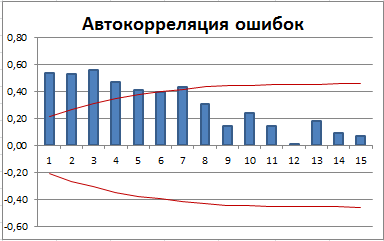
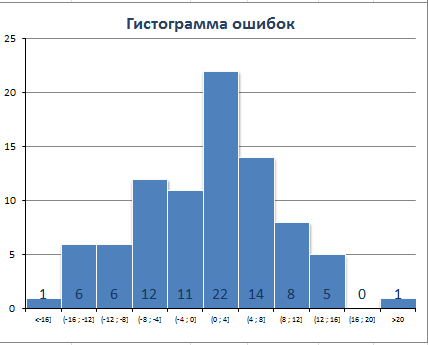
Очевидно, что при сглаживании рядов с сезонностью методом скользящего среднего ошибки не будут удовлетворять этим требованиям. Например:

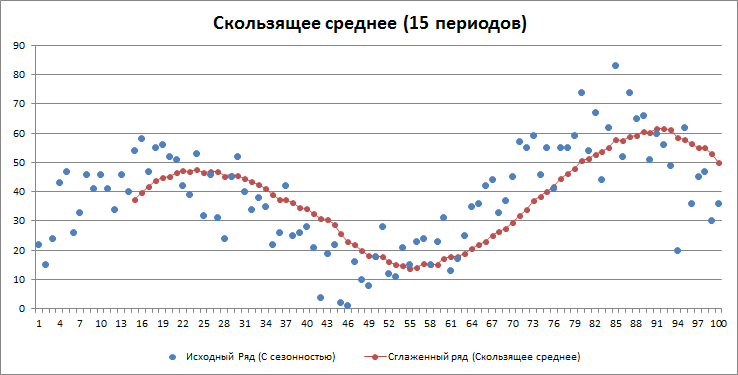
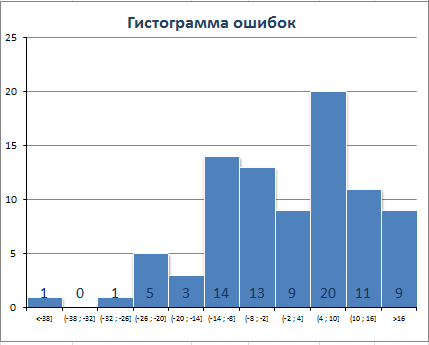
Очевидно, что имеется сдвиг вправо сглаженного ряда. Это приводит к тому, что гистограмма ошибок смещена влево (левый хвост длиннее).

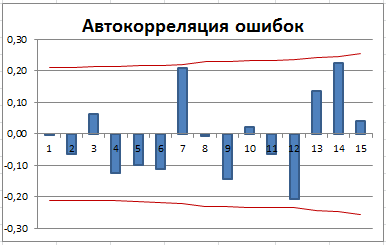
Имеется автокорреляция ошибок (для первых лагов значения автокорреляции вышли за границы 95% доверительного  интервала).

Совершенно иная картина для центрированного взвешенного среднего.

Вернемся к среднеквадратичной ошибке (RMSE).

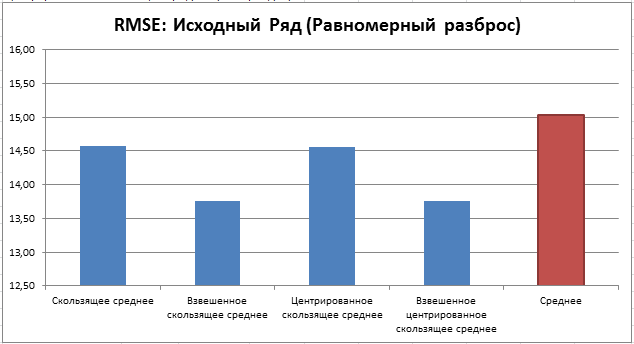
Сравним эту ошибку для различных типов исходного ряда. Сглаживание будем производить всеми 4-мя методами скользящего среднего (15 периодов) плюс вычислим среднеквадратичную ошибку относительно среднего значения исходного ряда. В итоге будем иметь 3 диаграммы:

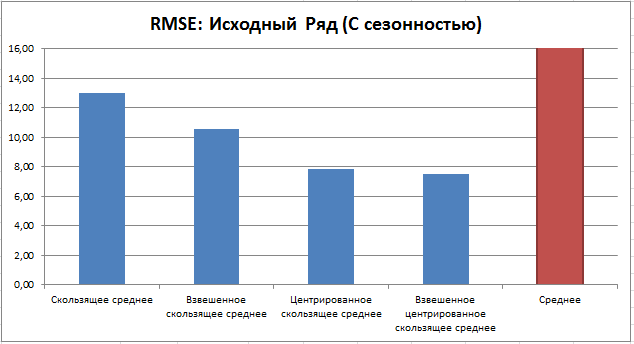
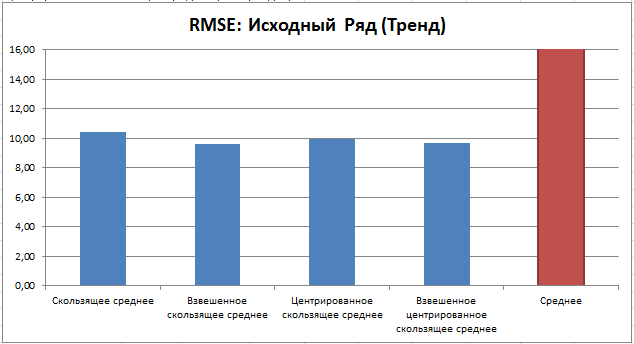
Для рядов с сезонностью (или цикличностью), похоже, наилучшим методом сглаживания является взвешенное центрированное скользящее среднее. 

В случае равномерного разброса наименьшую ошибку дают взвешенное скользящее среднее и взвешенное центрированное скользящее среднее.