Скользящее среднее используется для сглаживания краткосрочных колебаний с целью определения долгосрочного тренда. У этого метода есть несколько модификаций (центрированное, взвешенное), которые имеют положительные и отрицательные стороны. Рассмотрим как сделать соответствующие вычисления в MS EXCEL.  

Метод сглаживания краткосрочных колебаний – Скользящее среднее подробно рассмотрен в одноименной статье Скользящее среднее в MS EXCEL. Здесь остановимся на его модификациях.

При поиске оптимального количества периодов усреднения методом Скользящего среднего необходимо учитывать, что чем больше количество периодов усреднения тем:

•     глаже получаемый ряд (отфильтровываются колебания, скрывающие тренд);
•     больше увеличивается лаг (ряд скользящего среднего запаздывает относительно тренда исходного ряда). Это проявляется в смещении вправо «поворотных» точек, когда меняется направление тренда. 

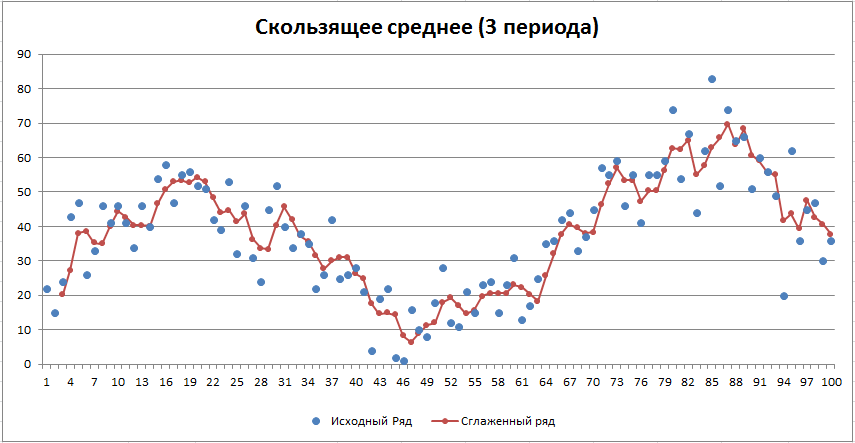
На первой картинке (3 периода) ряд скользящего среднего содержит многочисленные колебания, но тренды обоих рядов не смещены относительно друг друга (см. файл примера на лист Скользящее среднее).
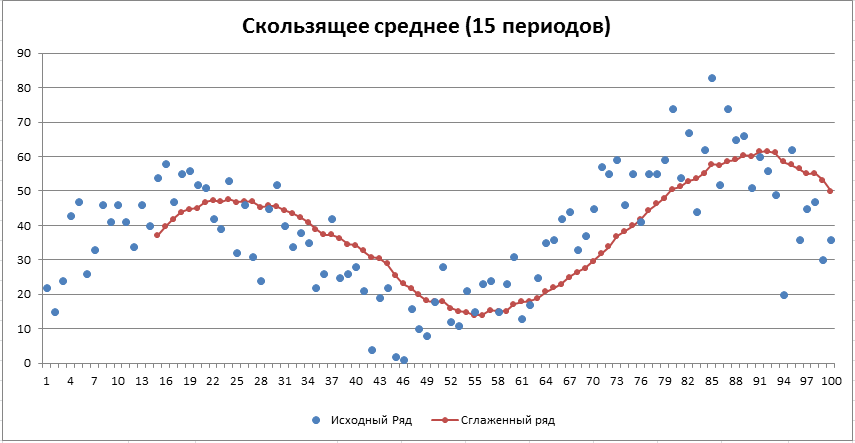
На второй картинке (15 периодов) ряд скользящего среднего сглажен, но тренды обоих рядов существенно смещены относительно друг друга.
Для устранения сдвига сглаженного ряда вместо простого скользящего среднего используют центрированное скользящее среднее.

Центрированное скользящее среднее

Для компенсации сдвига сглаженного ряда относительно исходного используют центрированное скользящее среднее. В этом случае значения сглаженного ряда получают путем усреднения как более ранних, так и более поздних значений.
Например, для 3-х периодов усреднения значения такого сглаженного ряда получают так:

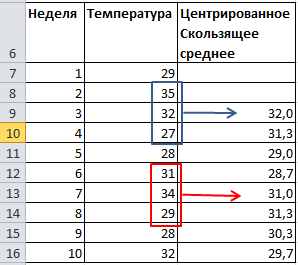
Y_{центр.скол.i}=(Y_i+1+ Y_i+ Y_i-1)/3 

См. файл примера на листе Центрированное-3 периода построение сглаженного ряда в случае 3-х периодов. При четном количестве усреднений используют метод двойного усреднения.

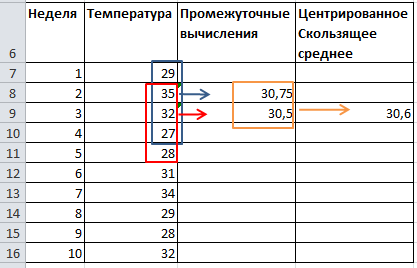
Например, для 4-х периодов усреднения значения такого сглаженного ряда получают так:

Y_{центр.скол.i} = ((Y_i+2 +Y_i+1+ Y_i+ Y_i-1)/4 + (Y_i+1 +Y_i+ Y_i-1+ Y_i-2)/4)/2 

или просто среднее всех 8-ми значений исходного ряда:
Y_{центр.скол.i} = (Y_i+2 + Y_i+1+ Y_i+ Y_i-1 + Y_i+1 +Y_i+ Y_i-1+ Y_i-2)/8 =(Y_i+2 + 2*(Y_i+1+ Y_i+ Y_i-1) + Y_i-2)/8

В файле примера на листе Центрированное реализовано построение сглаженного ряда с настраиваемым периодом усреднения:

=ЕСЛИ(ИЛИ(A11<(ЦЕЛОЕ($C$8/2)+1);A11>($G$8-ЦЕЛОЕ($C$8/2)));НД();
СРЗНАЧ(
СМЕЩ(B11;-(ЦЕЛОЕ($C$8/2));;$C$8);
СМЕЩ(B11;-(ЦЕЛОЕ($C$8/2))+ЕЧЁТН($C$8);;$C$8)))

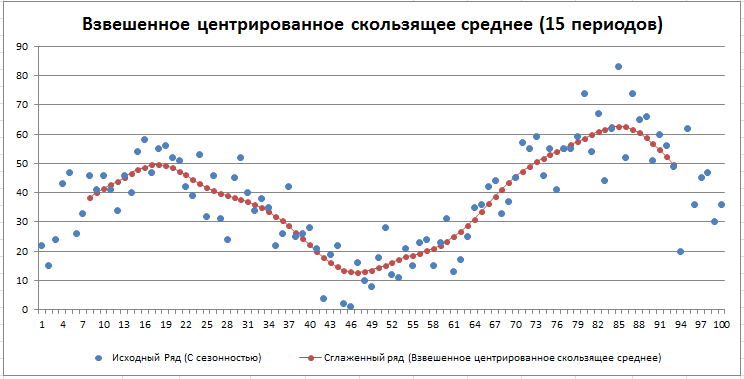
В итоге для 15 периодов сглаженный ряд будет иметь вот такой вид.

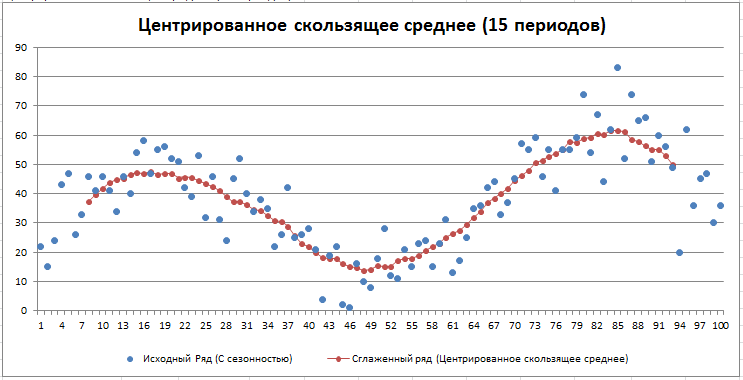
Очевидно, смещения вправо не наблюдается как у простого сглаженного среднего.

Примечание: Так как для вычисления центрированного скользящего среднего требуется знать как более ранние, так и более поздние значения, то становится очевидным, что такой метод сглаживания нельзя использовать для прогнозирования.

Взвешенное скользящее среднее

В рассмотренных выше методах вклад всех значений Y_i+1; Y_i; Y_i-1 в расчет скользящего среднего был одинаков, т.е. удаленные на разное количество периодов значения влияли одинаково на вычисление скользящего среднего.

В методе взвешенного скользящего среднего значения от более отдаленных периодов учитываются в меньшей степени, чем от близких.

Вспомним как рассчитывалось скользящее среднее в случае усреднения за 3 периода: 

Y_скол.i=(Y_i+ Y_i-1+ Y_i-2)/3 

Таким образом, при усреднении значения исходного ряда учитывались в равной степени. Формулу можно переписать следующим образом:

Y_скол.i=1/3*Y_i+ 1/3*Y_i-1+ 1/3*Y_i-2

1/3 – это вес значений исходного ряда, которые используются при усреднения. 

Взвешенное скользящее среднее является модификацией скользящего среднего: при его расчете веса различных периодов имеют различный вес (более отдаленные периоды, как правило, имеют меньший вес). Сумма весов должна быть равна 1.

Примечание: Сумма весов может отличаться от 1, но в этом случае каждое значение сглаженного ряда нужно разделить на эту сумму. 

В файле примера на листе Взвешенное-3 периода вычислим Взвешенное скользящее среднее для 3-х периодов со следующими весами:

Y_скол.i=0,5*Y_i+ 0,4*Y_i-1+ 0,1*Y_i-2

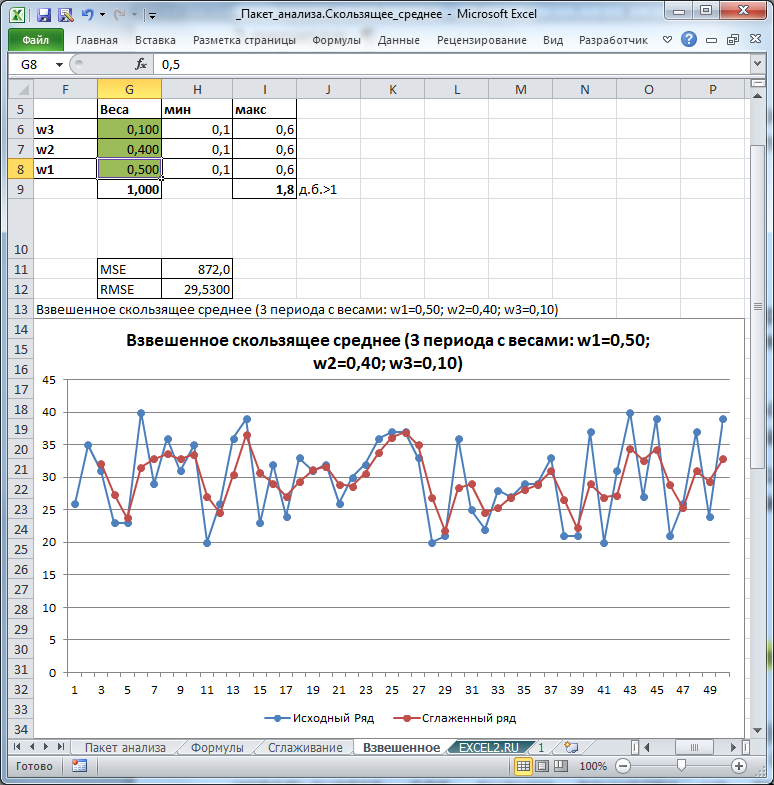
Для вычисления значений ряда используется формула =СУММПРОИЗВ(B11:B13;$F$6:$F$8), с помощью которой значения исходного ряда умножаются на соответствующие веса, затем производится сумма полученных произведений.

Веса для каждого периода усреднения выбираются из условий задачи или могут быть оптимизированы путем минимизации суммы квадратов ошибок (англ. Sum of Squared Errors - SSE), которая вычисляется по формуле: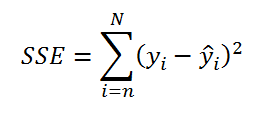

Суммирование идет по всем точкам сглаженного ряда (номер первой точки сглаженного ряда равен периоду усреднения, т.е. n (для данного метода), N – общее количество точек исходного ряда.

Для подбора оптимальных весов можно использовать инструмент MS EXCEL Поиск решения.

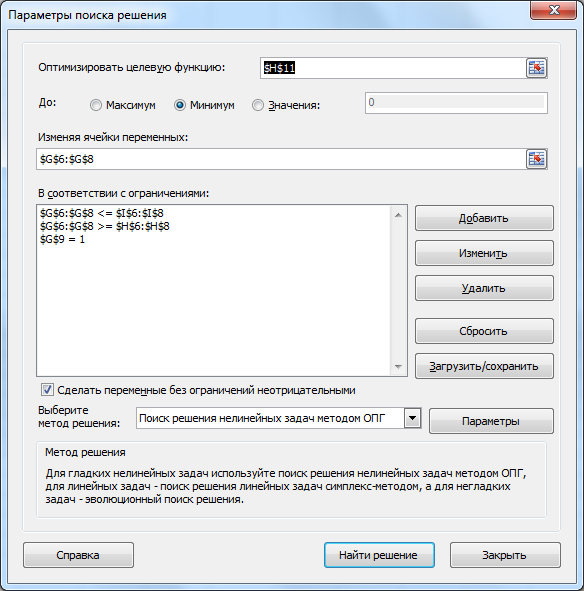
В качестве ограничений используются минимальные и максимальные значения весов, кроме того сумма весов должна быть =1. Если не задать минимальные и максимальные значения весов, то все веса, кроме веса ближайшего периода будут установлены Поиском решения равными 0. Т.к. в этом случае среднеквадратичная ошибка будет минимальна и =0 (оба ряда просто совпадут).

Взвешенное скользящее среднее с настраиваемым количеством периодов усреднения приведено в файле примера на листе Взвешенное. В этом случае потребуется также автоматический расчет весов. Расчет весов выполнен по формуле wi=i/s, где s – сумма номеров периодов усреднения. Например, если периодов усреднения 3, то сумма номеров периодов усреднения равна 6=3+2+1. При расчете первой точки сглаженного ряда w1=1/6, w2=2/6, w3=3/6. Сумма весов равна 1. w3 имеет максимальной вес, т.к. по времени соответствующая точка №3 ближе всего к первой точке сглаженного ряда. Конечно, можно использовать и другие формулы или распределения: одной из разновидностей взвешенных методов является экспоненциальное сглаживание.

Метод Взвешенного скользящего среднего также как и просто скользящее среднее имеет значительный лаг при больших значениях периода усреднения, т.е. когда ряд скользящего среднего запаздывает относительно тренда исходного ряда. Этого недостатка лишена следующая модификация - Взвешенное центрированное скользящее среднее.

Взвешенное центрированное скользящее среднее

При расчете Центрированного скользящего среднего, рассмотренного выше, также можно изменить веса периодов усреднения. 
Это можно сделать с помощью формулы:

=ЕСЛИ(ИЛИ(A11<(ЦЕЛОЕ($C$8/2)+1);A11>($G$8-ЦЕЛОЕ($C$8/2)));НД();
СРЗНАЧ(
СУММПРОИЗВ(СМЕЩ(B11;-(ЦЕЛОЕ($C$8/2));;$C$8);СМЕЩ($S$12;;;$C$8));
СУММПРОИЗВ(СМЕЩ(B11;-(ЦЕЛОЕ($C$8/2))+ЕЧЁТН($C$8);;$C$8);СМЕЩ($S$12;;;$C$8)))/$V$14)

Как и для взвешенного скользящего среднего, значения от более отдаленных периодов учитываются в меньшей степени, чем от близких.

Примечание: Для генерации весов в формуле использовано нормальное распределение.

В статье Анализируем ошибки моделей сглаживания временных рядов будет показано, что при увеличении количества периодов усреднения (n), погрешности будут расти практически монотонно: сначала за счет постепенного «выпрямления» сглаженной кривой по сравнению с исходным «пилообразным» графиком, затем и за счет его сдвига вправо. Сдвиг вправо сглаженной кривой особенно актуален для рядов с трендом и рядов с сезонностью.

Примечание: Оценка качества полученной модели для прогнозирования по кривым роста производится при проверке адекватности и оценки точности модели. В проверку адекватности входит: проверка независимости (отсутствие автокорреляции по критерию Дарбина-Уотсона), проверка случайности, соответствие остатков временного ряда случайному распределению(R/S критерий), равенство 0 средней ошибки.