Процентили в EXCEL

Рассмотрим понятие процентиля, функцию ПРОЦЕНТИЛЬ.ВКЛ() , процентиль-ранг и построим кривую процентилей.

Сначала разберемся на примерах, что такое процентиль , затем рассмотрим соответствующие функции MS EXCEL.

Задача. Проектируют койку на круизном лайнере. Необходимо, чтобы 95% пассажиров помещались на койке в полный рост. Как вычислить длину койки?

Для решения задачи потребуется найти рост, ниже которого 95% населения. Для этого нужно сделать репрезентативную выборку , скажем, из 2000 человек, отсортировать значения выборки по возрастанию , потом определить значение с позицией равной 1901 (2000*95%+1). Пусть найденный рост оказался равен 190 см. Ответ : Длина койки должна быть 190 см (+ запас для комфортного размещения на койке).

Значение 190 см называется 95%-й процентилью данной выборки , т.е. 95% опрошенных людей имеет рост <190 см.

Примечание : Найденное значение (190см) является оценкой 95%-й процентили всей генеральной совокупности , из которой взята выборка .

СОВЕТ : Понятие процентиля связано с понятием квантиля функции распределения . Поэтому имеет смысл освежить в памяти понятия функции распределения и обратной функции .

На основании вышесказанного сформулируем определение для процентили : K-й Процентиль представляет такое собой значение Х в наборе данных, которое разделяет набор на две части: одна часть содержит K процентов данных, меньших Х , а другая часть содержит все остальные значения набора (т.е. 1- K процентов данных б о льших Х).

Приведем алгоритм для нахождения k -й процентили выборки:

• отсортировать значения выборки по возрастанию (пусть в выборке всего N значений);
• найти такую позицию в списке , для которой k% значений оказалось бы меньше этого значения. Это можно сделать с помощью формулы N*k%+1 (затем, округлить его до целого );
• значение, находящееся в этой позиции, и будет k -й процентилью (примерно), т.к. k% значений массива данных будет меньше этого значения.

Примечание : Более точный алгоритм расчета процентилей дан ниже в разделе про функцию ПРОЦЕНТИЛЬ.ВКЛ() .

Еще одна задача . Зачет «автоматом» поставят только тем студентам, которые в течение семестра набрали в течение семестра больше баллов, чем 90%-я Процентиль (другими словами 10% лучшим студентам поставят зачет «автоматом»).

Так как порог установлен в процентилях , то заданному % студентов придется сдавать экзамен вне зависимости от набранных баллов (т.е. 90% студентов в любом случае будут сдавать экзамен). А вот если бы порог был установлен в абсолютных значениях, например, 380 баллов из 400, то вполне вероятна ситуация, когда половине студентов поставили бы «автоматом» (если бы они, конечно, набрали бы больше 380 баллов). Или наоборот, при общих слабых результатах ни один студент не получил бы зачет «автоматом». Установка порога в процентилях создает предпосылки здоровой конкуренции (или, наоборот, сговора: даже если никто особо не учился, то в любом случае 10% получат зачет «автоматом»).

Решим эту задачу, используя заданные значения выборки . Пусть всего 120 студентов, значения баллов за семестр разместим в диапазоне A8:A127 (см. Файл примера , лист Пример-Студенты ). Максимальный суммарный балл = 400. Порог получения зачета «автоматом» - больше баллов, чем 90%-я Процентиль .

Понятно, чтобы определить тех студентов, которые получат зачет «автоматом» нужно отсортировать их по набранным баллам и отобрать 10% (т.е. 12 студентов) с максимальными баллами. Но, чтобы студенты сами определились, начинать ли им готовиться к экзамену или нет, достаточно сообщить им проходной балл (90%-ю процентиль ). Рассчитаем этот проходной балл.

Для наглядности построим Гистограмму распределения с накоплением .

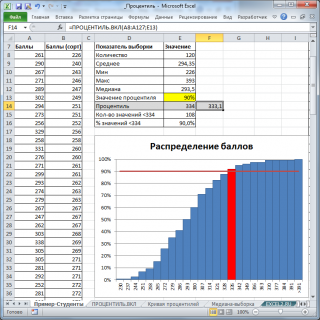
90%-ю процентиль можно найти с помощью формулы =НАИМЕНЬШИЙ(A8:A127;ЦЕЛОЕ(120*0,9)+1)

Эта формула создана на основе алгоритма, приведенного выше. Результат формулы - 334 балла.

Как видно из рисунка выше, количество значений массива (студентов), у которых баллы хуже, действительно равно 108 (90% от 120). Следовательно, как и предполагалось, 12 студентов получат зачет «автоматом».

Примечание : Найденное значение процентили 334 является приблизительным. Точное значение дает формула =ПРОЦЕНТИЛЬ.ВКЛ(A8:A127;0,9) , которое равно 331,4. О том как работает функция ПРОЦЕНТИЛЬ.ВКЛ() читайте ниже.

Как показывает опыт, для данных выборки K -я процентиль не всегда отделяет точно К процентов значений, которые меньше ее. Например, в нашем примере найдем 80%-ю процентиль. Оказывается, что только 79% значений меньше 80%-й процентили (318). Это происходит из-за округления. Для выборок с большим количеством значений (>100) обычно наблюдается хорошее соответствие. Повторы значений также могут привести к несоответствию значения процентиля и соответствующего % значений (см. ниже).

Примечание : Процентили часто называют перцентилями (с этим соглашается и MS WORD) или центилями . В версии MS EXCEL 2007 и более ранних использовалась функция ПЕРСЕНТИЛЬ() , которая оставлена для совместимости. Но, начиная с версии EXCEL 2010, появились функции ПРОЦЕНТИЛЬ.ВКЛ() и ПРОЦЕНТИЛЬ.ИСКЛ() – английское название PERCENTILE.EXC(), а Условное форматирование предлагает настроить правило с использованием именно процентилей . В свою очередь, надстройка Пакет Анализа имеет инструмент Ранг и Персентиль . Google также отдает предпочтение процентилям , выдавая гораздо больше результатов на запрос «процентиль», чем на запрос «перцентиль» (на начало 2016 года).

Таким образом, для процентилей используется 3 названия: процентиль (MS EXCEL, Google) , персентиль (MS EXCEL) , перцентиль (MS WORD) .

Ниже детально рассмотрим как работает функция ПРОЦЕНТИЛЬ.ВКЛ() и создадим ее аналог с помощью альтернативной формулы. Также рассмотрим функцию ПРОЦЕНТРАНГ.ВКЛ() и кривую процентилей .

СОВЕТ : Нижеследующие разделы следует читать пользователям, владеющими базовыми понятиями математической статистики (случайная величина, функция распределения) .

Функция ПРОЦЕНТИЛЬ.ВКЛ()

Начиная с версии MS EXCEL 2010 для расчета процентилей используется функция ПРОЦЕНТИЛЬ.ВКЛ() – английское название PERCENTILE.INC(). В более ранних версиях MS EXCEL использовался ее аналог - функция ПЕРСЕНТИЛЬ() .

Напомним определение процентиля , данное выше: K-й Процентиль представляет такое собой значение Х в наборе данных, которое разделяет набор на две части: одна часть содержит K% данных, меньших Х , а другая часть содержит все остальные значения набора (т.е. 1- K % данных б о льших Х).

Разберем детально как работает функция ПРОЦЕНТИЛЬ.ВКЛ() .

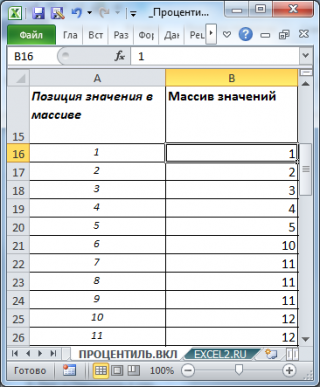
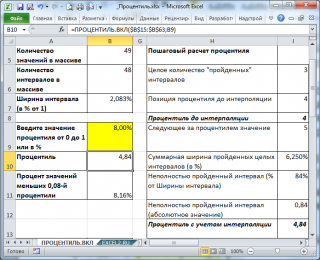
Пусть имеется массив значений ( выборка ). В массиве 49 значений, массив расположен в диапазоне B15:B63 , имеются повторы значений , массив для удобства отсортирован по возрастанию (см. файл примера , лист ПРОЦЕНТИЛЬ.ВКЛ ).

Рассчитаем 0,08-ю процентиль ( 8%-процентиль ) с помощью формулы =ПРОЦЕНТИЛЬ.ВКЛ(B15:B63; 0,08) . Получим, что 0,08-я процентиль равна 4,84.

Проанализируем, что мы получили.

• Во-первых, значения 4,84 нет в массиве (есть 4 и 5), т.е. функция ПРОЦЕНТИЛЬ.ВКЛ() интерполирует значения.
• Во-вторых, процент значений меньших 4,84 равен не точно 8%, а 8,16%=4/49*100% (т.к. всего 4 значения в массиве меньше 4,84). Это произошло, т.к. в выборке относительно мало значений.
• Другой причиной расхождения могут стать повторы. Например, заменив, первые 4 значения в массиве (т.е. 1; 2; 3; 4) числом 5, мы получим вместо 8,16% - 0%. Это произошло потому, что теперь 0,08-я процентиль равна 5, а в выборке нет ни одного значения меньше 5.

Как видно из рисунка ниже первое значение ( минимальное , равное 1) является 0-й процентилью .

Соответственно, 1-й процентилью (100% процентилью ), является максимальное значение равное 120 (см. файл примера лист ПРОЦЕНТИЛЬ.ВКЛ).

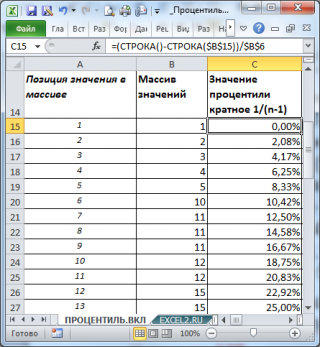
Как видно из рисунка, следующее за минимальным значением (т.е. число 2) является 0,0208-й процентилью . Значение 0,0208 или 2,08% - это (k-1)*1/(n-1), где n – это количество значений в массиве (в нашем массиве n=49), а k – это позиция числа в массиве (в данном случае k=2, где 2 – это позиция, а не само число).

Поясним эту формулу. Для вычисления процентили принимается, что весь диапазон значений массива (от мин до макс) разбит n значениями на равные интервалы (их всего n-1). Соответственно, 1/(n-1), это «ширина» интервала (весь диапазон равен 1 или 100%). Обратите внимание, что «ширина» интервала не зависит от данных, а только от их количества. В нашем случае «ширина» интервала равна 0,0208 или 2,08%.

Приведем алгоритм расчета 12,50%-процентили функцией ПРОЦЕНТИЛЬ.ВКЛ() (см. ячейку С21 ):

• ПРОЦЕНТИЛЬ.ВКЛ() определяет «ширину» интервала (в долях или процентах): =1/(49-1)=0,0208;
• подсчитывает Количество интервалов , которые были укладываются в 12,50%, т.е. =12,50%/2,08%=6 (значение процентиля кратно ширине интервала, т.е. делится нацело);
• 6-й интервал располагается между числами массива 10 и 11. Верхняя граница последнего 6-го интервала равна 11;
• Следовательно, 12,50%-я процентиль равна 11 (см. ячейку B 21 ).

По аналогии с непрерывной функцией распределения (см. статью про квантили ), получается, что 12,50% значений должно быть меньше полученного числа 11 (в соответствии с определением процентиля ). Фактически получается, что таких значений 6 (1; 2; 3; 4; 5; 10) и процент значений меньших 11 равен 12,24%=6/49 (причины расхождения: повторы и небольшое количество значений).

Если значение процентиля не кратно ширине интервала (ширина интервала равна 1/(n-1)), то имеет место интерполирование. Например, вспомним результат вычисления 0,08-й процентили равный 4,84. Значение процентили (т.е. не результат, а %) равно 0,08 (8%), что соответствует 3-м целым интервалам (8%/2,08%= 3 ,84) и некой доли (0,84) от ширины следующего интервала. Границами этого «неполного» интервала являются значения 4 ( 0,0625-я процентиль ) и 5 ( 0,0833-я процентиль ). Т.к. разница между 5 и 4 равна 1, то умножая «пройденную» долю интервала (0,84) на длину интервала в абсолютных значениях (=5-4=1), получаем 0,84. В итоге получаем 4,84: 4 – левая граница интервала + часть следующего (5-4)*0,84.

Если бы в массиве вместо 5 было значение 6, то значение 0,08-й процентили было бы равно 5,68 (4 – левая граница интервала + (6-4)*0,84=1,68).

Альтернативный расчет процентили с помощью формул приведен в файле примера .

Примечание : Некоторые значения процентилей имеют специальные названия:

• 25-я процентиль называется 1-й квартилью;
• 50-я процентиль называется Медианой (2-я квартиль);
• 75-я процентиль называется 3-й квартилью.

Функция ПРОЦЕНТРАНГ.ВКЛ() и Кривая процентилей

Функция ПРОЦЕНТРАНГ.ВКЛ() используется для оценки относительного положения значения в массиве. Для заданного значения функция вычисляет сколько значений в массиве меньше или равно ему. Точнее - какой процент значений массива меньше или равен ему. Результат функции называется процентиль-ранг (percentile rank) . Понятно, что для максимального значения процентиль-ранг равен 0,00%, а для наименьшего - 100% (все значения массива меньше или равны ему).

Функция ПРОЦЕНТРАНГ.ВКЛ() , английская версия – PERCENTRANK(), является, в каком-то смысле, обратной функции ПРОЦЕНТИЛЬ.ВКЛ() : т.е. задавая в качестве аргумента значение из массива, функция ПРОЦЕНТРАНГ.ВКЛ() вернет значение процентили кратной 1/(n-1).

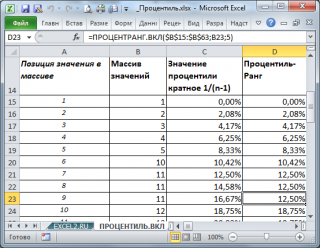
Как видно из рисунка выше, для повторяющихся значений функция ПРОЦЕНТРАНГ.ВКЛ() вернет, естественно, одинаковые значения. Также поступает функция РАНГ.РВ() или РАНГ() (см. статью Функция РАНГ() в MS EXCEL ).

Действительно, функции РАНГ.РВ() и ПРОЦЕНТРАНГ.ВКЛ() очень похожи. Первая возвращает позицию числа в массиве в зависимости от его значения. Вторая, в принципе, делает тоже самое, но результат выводится в % от общего количества значений в массиве.

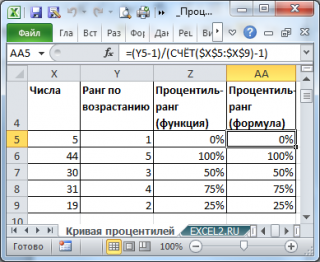
Как видно из картинки выше, чтобы получить процентиль-ранг необходимо значение ранга уменьшить на 1 и разделить на n-1. Значение ранга , естественно, должно быть отсортировано по возрастанию .

По выборке можно оценить функцию распределения Генеральной совокупности , из которой взята данная выборка. Для этой цели построим Кривую процентилей (percentile curve или percentile rank plot). 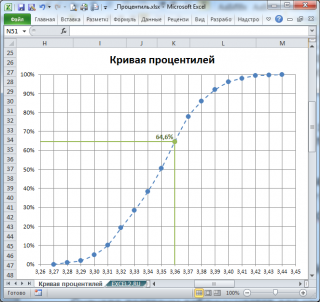Кривая процентилей представляет собой график зависимости процентиль-ранга от значений выборки .

Возьмем выборку состоящую из 100 значений (см. файл примера лист Кривая процентилей ). Значения содержатся в диапазоне А5:А104 .

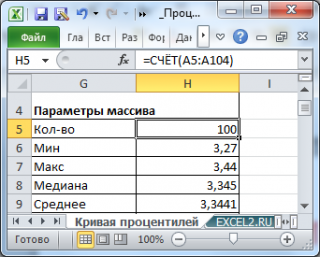
Сначала построим таблицу частот для каждого из значений выборки .

Примечание : В отличие от Гистограммы , где кумулятивная таблица частот строится для интервалов значений, таблицу частот для Кривой процентилей строят для каждого из значений выборки .

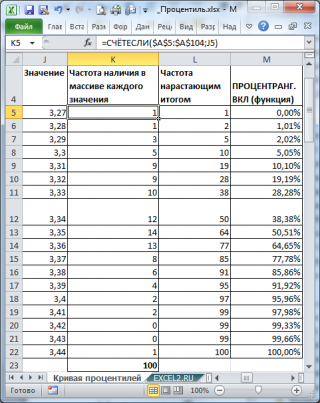
Из таблицы видно (столбец Частота нарастающим итогом ), что примерно 1 процент значений меньше или равен значения 3,27, примерно 2 процента на уровне или ниже 3,28, 5 процентов на уровне или ниже 3,29, и так далее. График Кривой процентилей для этих данных приведен на картинке ниже.

СОВЕТ : Про построение графиков см. статью Основные типы диаграмм .

Следует отметить, что использование данных из таблицы приведет к точечному виду кривой (так как процентиль-ранг будет изменяться скачком для каждого значения выборки ). Поэтому, сглаженная кривая, построенная на основе этих данных будет лучше представлять оцениваемую функцию распределения (пунктирная кривая).

Построив пунктирную кривую, становится ясно, зачем нам пришлось вводить понятие процентиль-ранга: процентиль-ранг – является приблизительной вероятностью выбрать случайную величину меньше или равную соответствующему значению (сравните с определением функции распределения). Это, в частности следует из расчета процентиль-ранга по формуле =СЧЁТЕСЛИ($A$5:$A$104;"<"&A5)/ (СЧЁТ($A$5:$A$104)-1)

Обратите внимание, что при построении Кривой процентилей никакие значения из выборки не были удалены или сгруппированы. В этом смысле, построение Кривой процентилей это более точная процедура для оценки вида функции распределения , чем построение Гистограммы данных (так как информация не теряется в процессе построения). Правда, для этого требуется достаточно большая выборка (лучше >100 значений).

Примечание : Формула =(РАНГ.РВ(A5;$A$5:$A$104;1)-1)/ (СЧЁТ($A$5:$A$104)-1) эквивалентна формуле =ПРОЦЕНТРАНГ.ВКЛ($A$5:$A$104;A5;5)