Поиск решения EXCEL (6.2). Задача коммивояжера (полный граф, нелинейная модель)

Решим один из вариантов задачи коммивояжера для небольшого количества городов (5-10) с помощью надстройки Поиск решения. Построим нелинейную модель.

Рассмотрим задачу коммивояжера (англ. Travelling Salesman Problem, TSP) заключающуюся в отыскании самого короткого маршрута, проходящего через заданные города по одному разу с последующим возвратом в исходный город (также рассмотрим вариант без возврата).

Задача

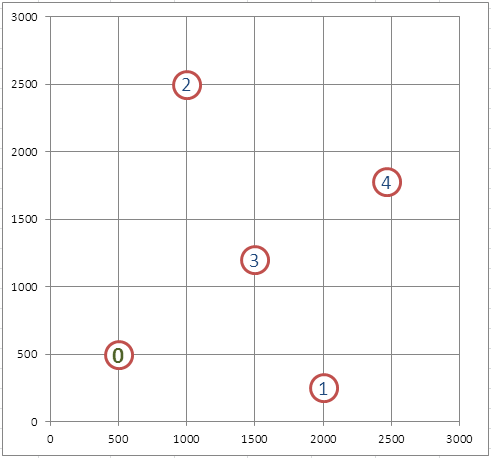
Найдем кратчайший путь между 5 городами, координаты которых известны. Рассмотрим замкнутый вариант задачи: коммивояжёру требуется посетить все города, после чего вернуться в исходный город.

Решение

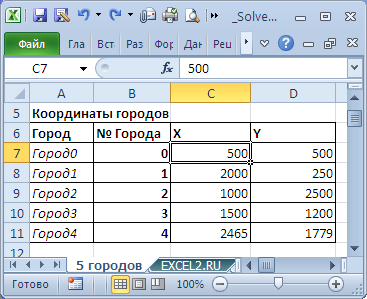
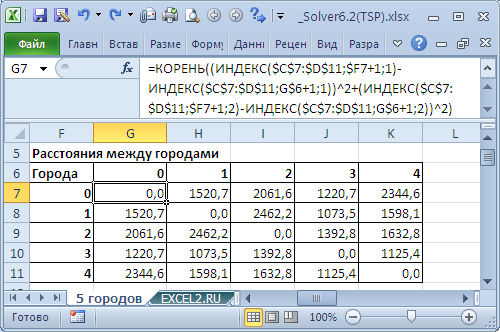
Так как даны координаты городов, то сначала найдем расстояния между ними (см. файл примера, лист 5 городов ).

Расстояния рассчитаем с помощью формулы: = КОРЕНЬ((ИНДЕКС($C$7:$D$11;$F7+1;1)-ИНДЕКС($C$7:$D$11;G$6+1;1))^2 +(ИНДЕКС($C$7:$D$11;$F7+1;2)-ИНДЕКС($C$7:$D$11;G$6+1;2))^2)

Теперь создадим модель для Поиска решения .

Совет : Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .

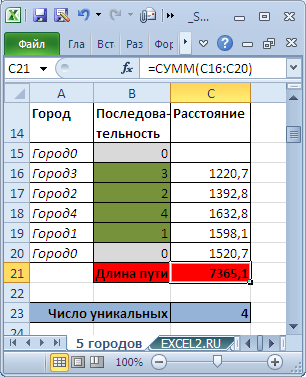
Переменные (выделено зеленым) . В качестве переменных модели следует взять номера городов. Так как начальная и конечная точка известны (Город0), то переменных будет 4. Ограничения (выделено синим) . Необходимо, чтобы номера городов не повторялись. Это означает, что количество уникальных (неповторяющихся) номеров городов должно быть равно 4. Для этого используется формула для подсчета уникальных значений : = СУММПРОИЗВ(1/СЧЁТЕСЛИ(B16:B19;B16:B19))

Целевая функция (выделено красным) . Длина маршрута должна быть минимальной.

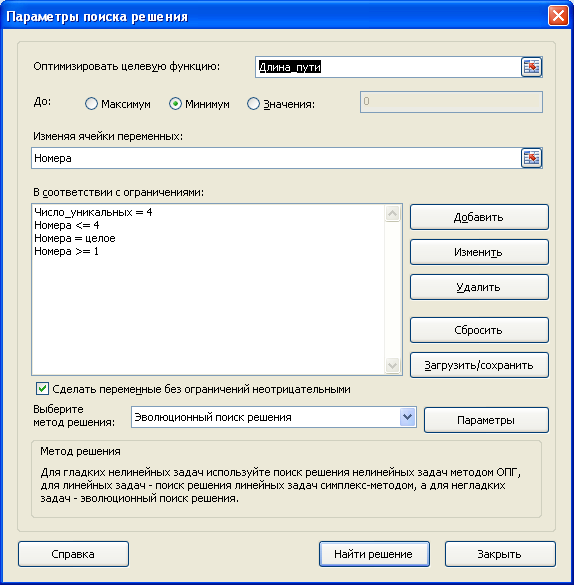
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .

Выберите Эволюционный метод поиска решения, т.к. созданная модель не является линейной из-за наложенного на переменные ограничения.

Найденное Решение

Поиск решения найдет (должен найти) самый короткий маршрут, т.е. последовательность 0-1-4-2-3-0 (или обратную).

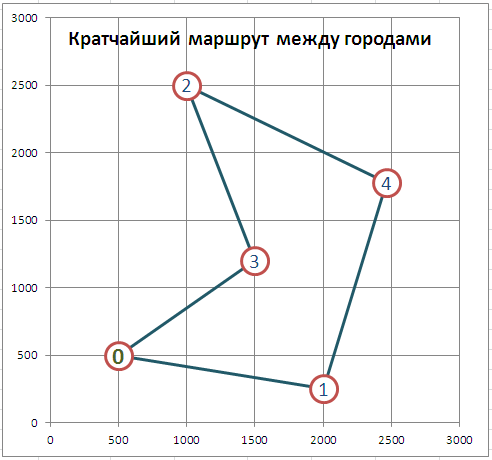
В этой простейшей задаче можно проверить, действительно ли этот маршрут имеет минимальную длину, путем перебора всех вариантов маршрутов. Это реализовано в файле примера .

Совет . Таблицы перебора перестановок от 1 до 5, от 1 до 6, … от 1 до 9 можно найти в этой статье Перебор всех возможных Перестановок в MS EXCEL .

Результаты Эволюционного метода сильно зависят от начальных условий и параметров его настройки (скорость изменения, размер совокупности). Повторный поиск, с теми же начальными условиями и параметрами, может привести к различным результатам. Убедиться в этом можно с помощью модели, созданной в файле примера на листе 11 городов.

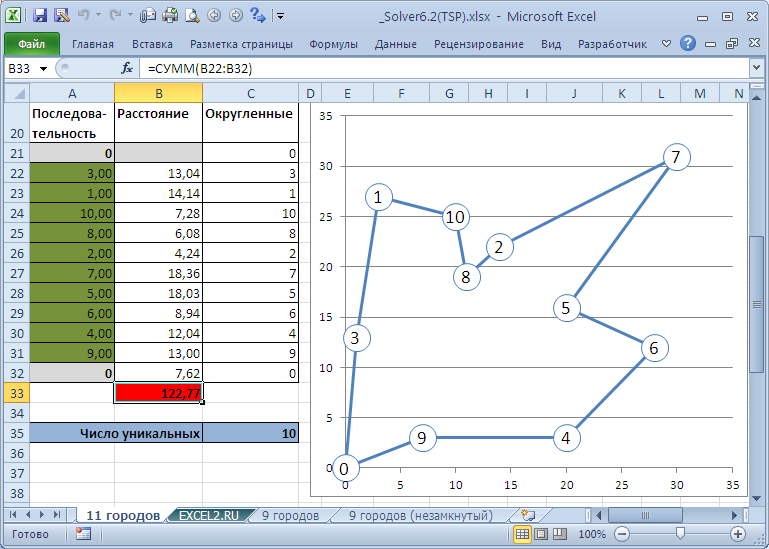
Обнулите значения переменных модели на Листе 11 городов, запустите Поиск решения. После окончания поиска (может занять несколько минут) опять обнулите значения переменных и перезапустите Поиск решения: найденные решения могут серьезно отличаться.

Совет . Иногда, для того чтобы улучшить найденное решение, помогает следующий прием: запустите Поиск решения , сохраните найденное решение, измените параметры поиска (например, размер совокупности), повторно запустите Поиск решения.

В файле примера также приведено решение задачи для замкнутого и незамкнутого маршрута посещения 9 городов. Решения найдены с помощью Эволюционного метода со следующими параметрами: Целочисленная оптимальность 0%, Использовать автоматическое масштабирование, Скорость изменения варьировалась 0,25-0,5; Размер совокупности варьировался 10-50. Оба решения проверены с помощью таблиц перебора всех маршрутов (см. таблицы перебора перестановок ). Если при первом прогоне Поиска решения не удавалось найти оптимальное решение, то он запускался повторно, при этом 1 или 2 параметра изменялись. После второго прогона оптимальное решение, как правило, было найдено.

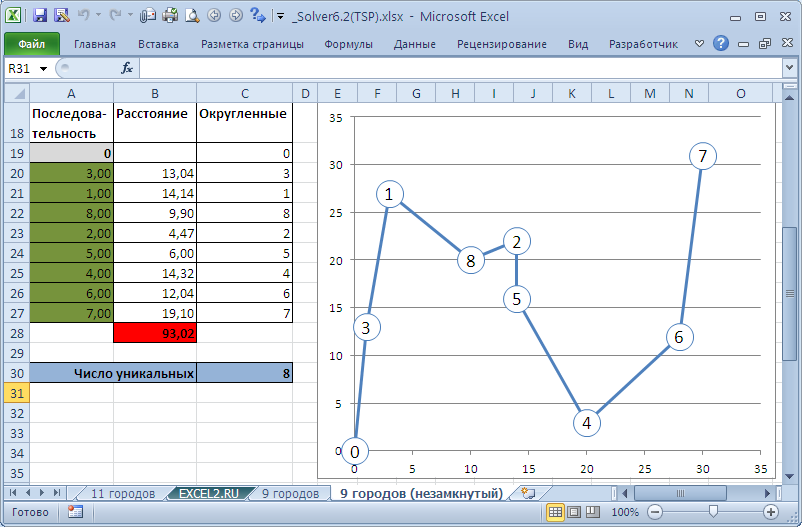
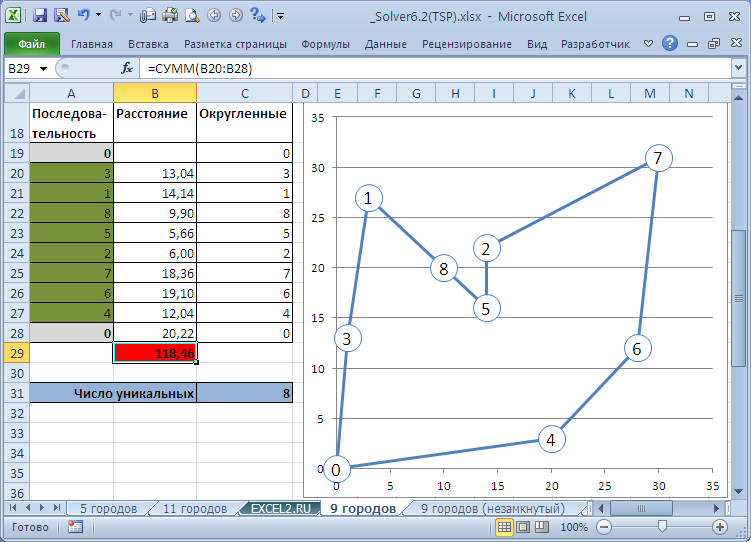
Вывод : задачу коммивояжера (граф полностью связный, гамильтоновый цикл) можно решить стандартным Поиском решения с помощью построения нелинейных моделей. При количестве вершин графа (городов) <10 найденное решение можно проверить с помощью таблиц перебора перестановок, т.к. Эволюционный метод не гарантирует, что найденный путь является кратчайшим. Поиск решения может продолжаться значительное время. Однако, более лучшей альтернативой решения этой задачи в MS EXCEL является построение линейной модели (см. статью Поиск решения MS EXCEL (6.3). Задача коммивояжера (полный граф, линейная модель) ) или написание программы на VBA.

Совет : Решение задачи о поиске кратчайшего пути между 2-мя заданными городами можно найти в статье Поиск решения MS EXCEL (6.4). Кратчайший путь (неполный граф, линейная модель) .