Сложение и вычитание матриц, умножение матриц на число в EXCEL
25 ноября 2015 г.
- Группы статей
- Матрицы
В этой статье рассмотрены операции сложения и вычитания над матрицами одного порядка, а также операции умножения матрицы на число. Примеры решены в MS EXCEL.
Операция сложения определена только для матриц одного порядка. Т.е. нельзя говорить о сложении матриц разной размерности. Также неопределена операция сложения матрицы и числа. Напротив, операция умножения матрицы на число определена.
Сумма двух матриц А и В - это матрица, элементы которой равны сумме соответствующих элементов матриц А и В.
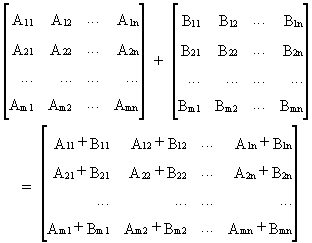
В MS EXCEL операцию сложения матриц реализовать элементарно.
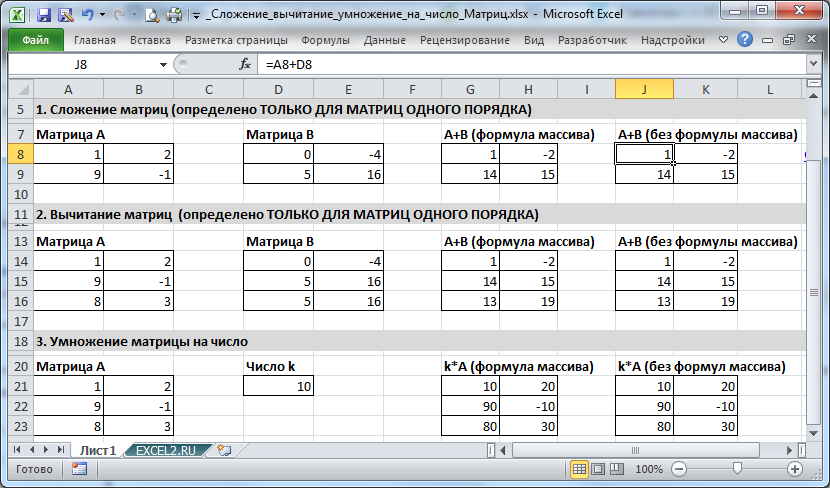
Поместив матрицу А размерности 2х2 в диапазон А8:В9 , а матрицу B той же размерности 2х2 в диапазон D8:E9, в ячейке J8 введем формулу =A8+D8 . Скопировав формулу в нужные ячейки, например, с помощью Маркера заполнения , получим матрицу А+В.
Аналогичного результата можно добиться с использованием формулы массива . Выделив диапазон G 8:H9 в Строке формул введите формулу =A8:B9+D8:E9 и нажмите CTRL+SHIFT+ENTER . Преимущество формулы массива состоит в том, что невозможно удалить отдельные элементы матрицы А+В (появится окно Невозможно удалить часть массива ).
Понятно, что операция вычитания матриц в MS EXCEL реализуется аналогично (см. файл примера ).
Умножение матриц на число
Операция умножения матрицы на число определена для матриц любого порядка.
Произведение матрицы А и числа k - это матрица, элементы которой получаются умножением всех элементов исходной матрицы А на число k.
В MS EXCEL это реализовано с помощью формулы =A21*$D$21 (предполагается, что матрица находится в диапазоне А21:В23 , а число в ячейке D21 ). Обратите внимание, что в формуле использована абсолютная адресация на ячейку с числом. Это позволяет при копировании формулы (для отображения всех элементов матрицы k*А) ссылаться на одну и ту же ячейку с числом.
Комментарии