Поиск решения EXCEL (4.3). Выбор места открытия нового представительства

Построим модель для принятия решения: компания планирует открыть в нескольких регионах свои представительства, куда будут поступать платежи от ее клиентов. Требуется определить оптимальный вариант открытия представительств, при котором суммарные расходы будут минимальны. Расчет будем проводить с помощью надстройки Поиск решения.

Задача

Компания планирует открыть в 6-и регионах свои представительства, куда будут поступать платежи от ее клиентов (представительства открываются в формате абонентных ящиков, см. примечание ниже). В качестве кандидатов на открытие абонентных ящиков рассматриваются 6 городов. Всего нужно открыть 6 абонентных ящиков - по одному для каждого региона. В городе можно открыть 1, 2 или более абонентных ящика для разных регионов, а можно и вовсе не открывать. Расходы на содержание абонентных ящиков в каждом городе разные (если в городе открыто их несколько, то оплачивается только 1). Средства от клиентов из Региона будут поступать в абонентный ящик Города с некоторой задержкой, в зависимости от Региона. Каждый день задержки стоит компании 6% от дневной суммы поступления. Требуется определить оптимальный вариант открытия абонентных ящиков, при котором суммарные расходы (содержание абонентных ящиков + потери из-за задержки платежа) будут минимальны (пример с сайта ]]> www.solver.com ]]> ).

Примечание . Абонентный ящик  - способ управления расчетами, при котором платежи клиентов компании поступают на специальный почтовый ящик, откуда периодически забираются банковскими служащими.

Создание модели

На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).

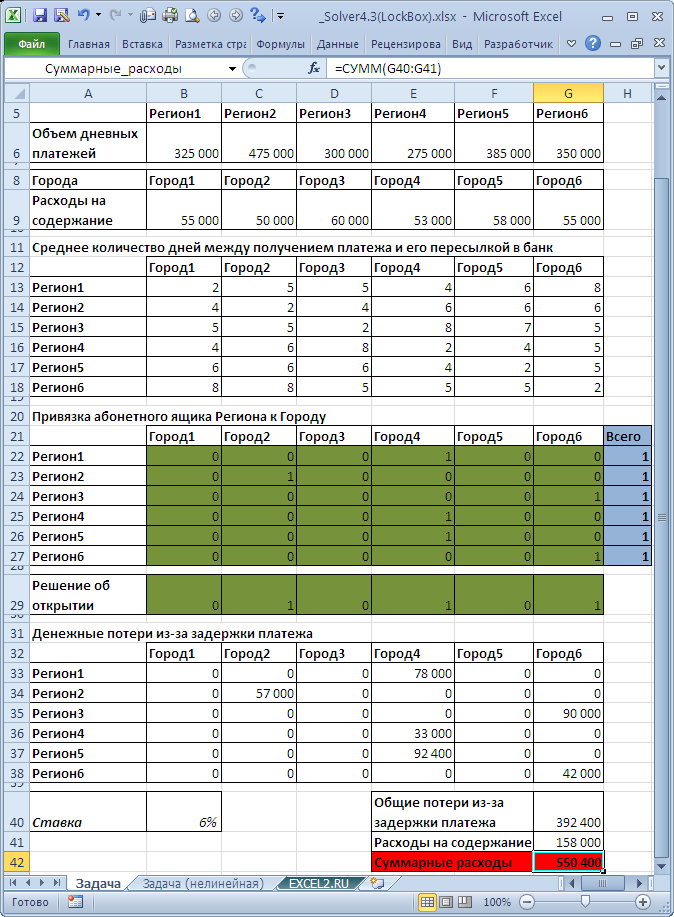
Переменные (выделено зеленым) . В качестве переменных модели следует взять привязку Региона к Городу: если представительство Региона размещено в Городе, то значение переменной =1, если нет, то 0. Вторым блоком переменных является решение об открытии в Городе, хотя бы 1 абонентного ящика. Эти переменные необходимы для подсчета расходов на содержание абонентного ящика, которые зависят только от Города, где он располагается. Если принято решение об открытии хотя бы одного абонентного ящика в Городе, то значение переменной =1, если нет, то 0. Ограничения (выделено синим) . Для каждого Региона должно быть открыто только по одному абонентному ящику. Целевая функция (выделено красным) . Суммарные расходы на содержание абонентных ящиков и потери из-за задержки платежей должны быть минимальны.

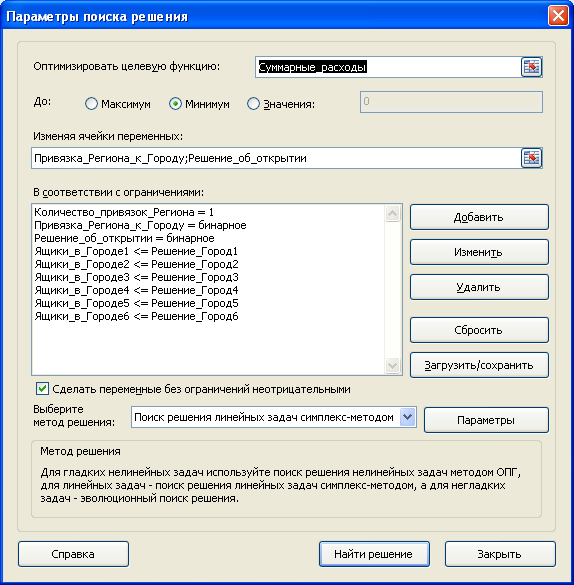
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .

Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .

О линейности модели

В результате расчета Поиск решения выдаст, что минимальные потери составят 550 400. Абонентные ящики необходимо открывать в Городах 2, 4 и 6. В Городах 4 и 6 открыть по несколько Абонентных ящиков.

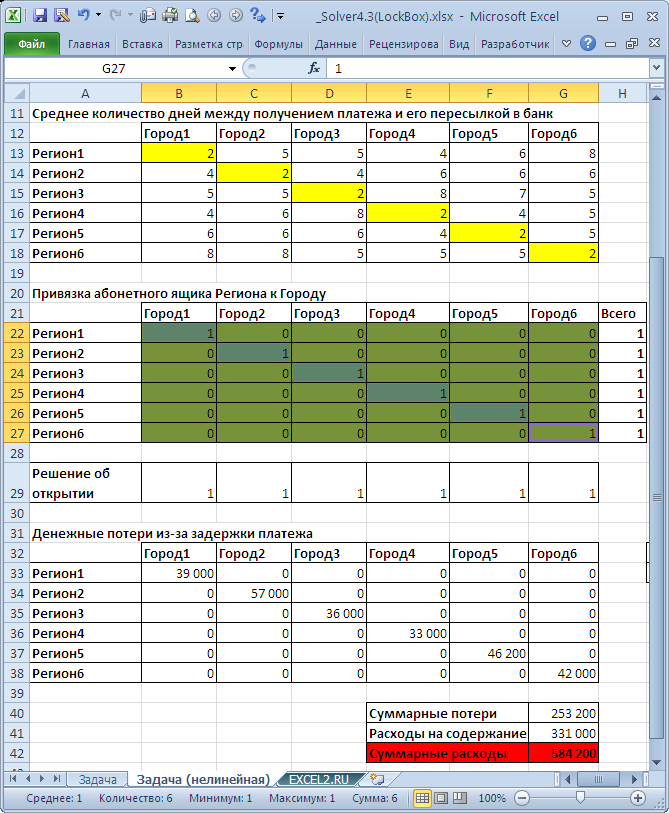
Теперь вернемся к переменным модели. Казалось бы, зачем нужен второй блок переменных? Ведь, зная привязку Региона к Городу мы всегда вычислим было ли принято решение об открытии в Городе, хотя бы 1 абонентного ящика. Например, это можно сделать с помощью формулы = ЕСЛИ(СУММ(Ящики_в_Городе1);1;) Однако, после замены этих переменных формулой, модель становится нелинейной. На листе Задача (нелинейная) файла примера приведен расчет такого варианта. Поиск решения в этом случае не гарантирует, что будет найдено глобально оптимальное решение, как в случае линейной модели. Т.е. в зависимости от начальных условий можно получить различные локально оптимальные решения. Например, при нулевых начальных значениях мы получим результат 685 900. Если в качестве начальных условий задать, что в Городах следует открыть Абонентные ящики для Регионов с наименьшим количеством дней задержки (см. рисунок ниже), то будет найдено решение 584 200. Поиск решения даже не будет пытаться изменить значения переменных, а просто скажет, что эти начальные условия соответствуют как минимум локально оптимальному решению. Отсюда можно сделать простой вывод: нужно стараться создавать линейные модели.