Поиск решения EXCEL (2.2). EOQ – экономичный размер заказа (с учетом ограничений)

Создадим модель для определения оптимального размера партии товара, при котором общие переменные затраты минимальны. Затраты связаны с процедурой заказа и хранением партии на складе, и зависят от размера партии. Также учтем ограничение, связанное с размером склада. Расчет будем проводить с помощью надстройки Поиск решения. Для простейшего случая задачи приведем аналитическое решение.

Задача основана на EOQ-модели (Economic Order Quantity, Экономичный размер заказа). Сначала рассмотрим классическую EOQ-модель, затем добавим ограничение, связанное с размером склада и найдем решение с помощью Поиска решения . (пример с сайта ]]> www.solver.com ]]> )

EOQ-модель

Изделия на склад поступают регулярно одинаковыми партиями размера Q (в каждой партии Q изделий), а со склада выходят по одному изделию (продаются или запускаются в производство). Предполагается, что количество изделий на складе уменьшается равномерно от Q до 0, а затем, происходит мгновенное пополнение склада новой партией (на величину Q) и так несколько раз в течение года, где D – это величина годового спроса на изделия. Соответственно, пополнение происходит D/Q раз в год. В этой модели 2 источника затрат:

• затраты, связанные с процедурой закупки партии товара;
• затраты на хранение изделий на складе.

Стоимость процедуры закупки одной партии фиксирована и равна K, она включает затраты на погрузку, разгрузку, доставку и пр. Суммарная стоимость закупки всех партий в течение года =K*D/Q. Годовая стоимость хранения одного изделия =h (включает содержание склада, охлаждение, страховку и пр.). Среднее количество изделий, хранящееся на складе =Q/2 (т.к. количество равномерно убывает от Q до 0), годовая стоимость хранения изделий =h*Q/2. Обратим внимание, что чем больше размер партии Q, тем выше расходы на хранение (=h*Q/2), но меньше стоимость закупки (=K*D/Q). Для определения оптимального размера партии (Q*) существует аналитическое решение. Общие затраты на хранение и закупку (TC): TC=K*D/Q+h*Q/2

После дифференцирования по Q определим Q* - размер партии, при которой TC минимальны.

Q*=SQRT(2*D*K/h) - формула Уилсона. На рисунке ниже приведены графики стоимости закупки, стоимости хранения и суммарные затраты (см. файл примера ).

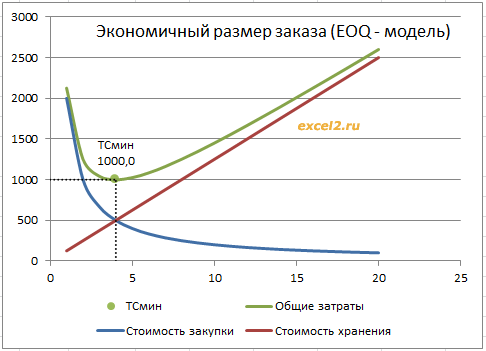
К сожалению, рассмотренная модель зачастую не отражает более сложную окружающую нас действительность: спрос подвержен изменениям, время исполнения закупочной процедуры не постоянно, на складе оставляют некий переменный запас изделий и др. В следующей модели мы учтем ограниченность размера склада. Для определения оптимального размера партии в данном случае нельзя будет применить Формулу Уилсона, но задачу можно решить с помощью Поиска решения . Покажем, как это сделать.

EOQ-модель с ограничением по объему склада

Усложним предыдущую задачу, добавив ограничение на объем склада, и рассмотрим поставку и хранение сразу 4-х разных изделий. У каждого изделия своя стоимость хранения и стоимость закупочной процедуры.

На рисунке ниже приведена модель, созданная для решения этой задачи (см. файл примера, лист EOQ (ограничен объем) ).

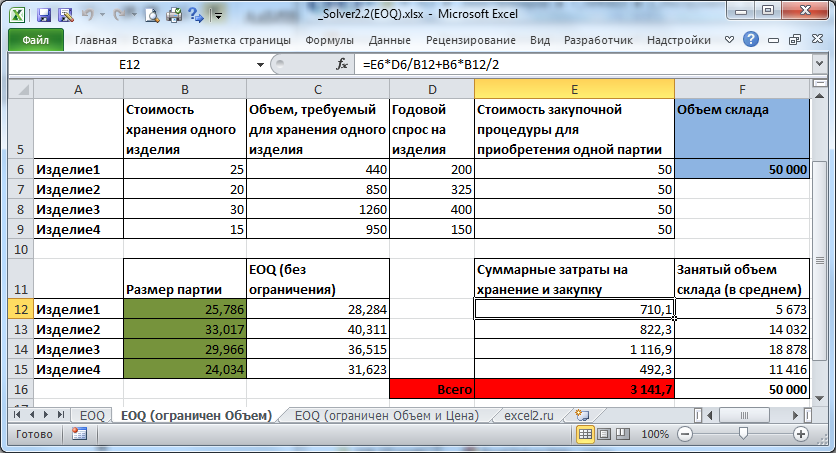
Переменные (выделено зеленым) . В качестве переменных модели следует взять количество изделий в партии (4 переменных для каждого изделия). Ограничения (выделено синим) . Объем склада не должен быть меньше, чем общий объем партий.

Примечание . Т.к. партии разных изделий приходят независимо друг от друга и количество изделий равномерно убывает от Q до 0, то в среднем количество изделий, находящихся на складе, будет равно половине партии (это допущение необходимо для сравнения с EOQ моделью).

Целевая функция (выделено красным) . Общая стоимость закупки и хранения, д.б. минимальна.

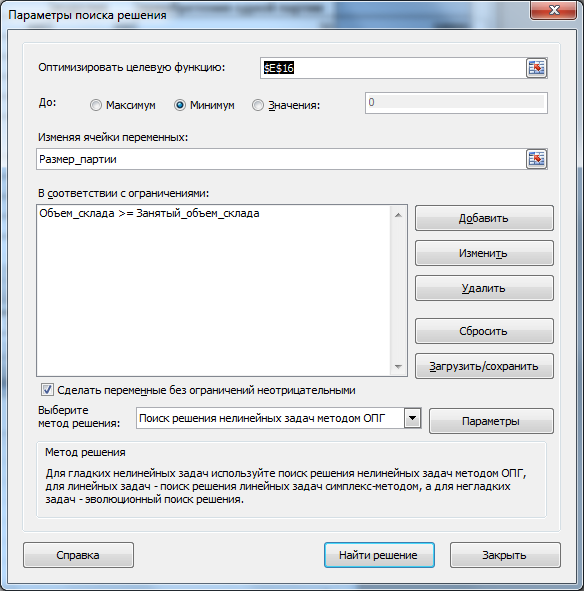
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .

Обратите внимание, что модель не линейная: Целевая функция (TC) зависит от переменных (Q) по нелинейному закону: TC=K*D/Q+h*Q/2 Поэтому в окне Поиска решения выберите метод для решения нелинейных задач. Формулы модели не должны содержать ошибок, поэтому не оставляйте ячейки переменных пустыми: в качестве начальных условий будут взяты 0 значения, что вызовет ошибку #ДЕЛ/0! Если ослабить ограничение (взять большой объем склада, скажем 500 000), то найденное решение будет близко или даже совпадать с расчетами, выполненными по Формуле Уилсона.

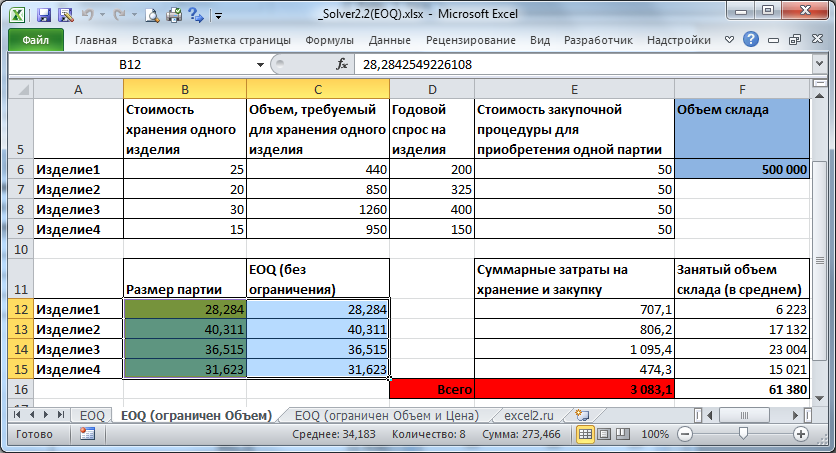
EOQ-модель с ограничением по объему склада и закупочной цене

Усложним предыдущую задачу, добавив ограничение на стоимость закупки изделий. Также потребуем, чтобы количество изделий в партиях было четным числом (см. файл примера, лист EOQ (ограничен объем и цена) ).

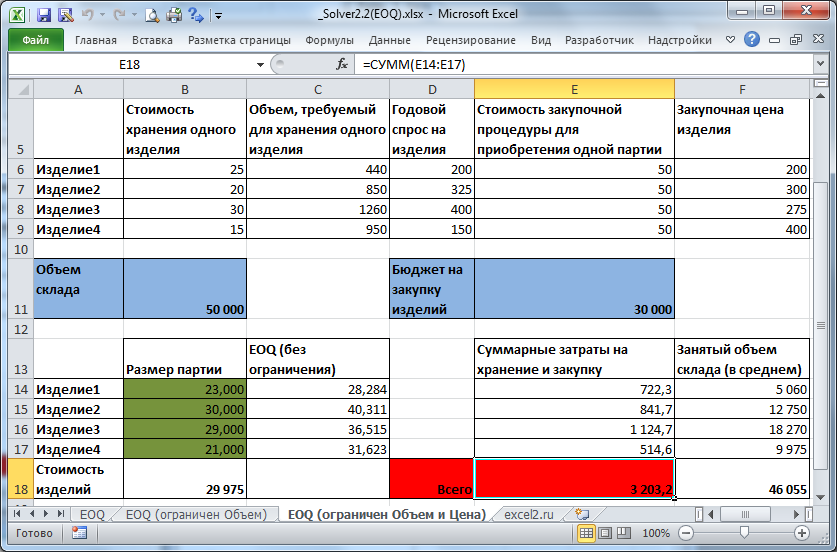
В параметрах Поиска решения можно установить Целочисленную оптимальность =0. При Целочисленной оптимальности =5% решение начинает сильно зависеть от начальных условий (установите сначала переменные равным 1, затем =26). В первом случае будет найдено решение 23, 30, 30, 20, а во втором 24, 31, 30, 19. Дело в том, что целевая функция в обоих случаях будет отличаться совсем незначительно (гораздо менее 5%).

Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .