Поиск решения EXCEL (1.5). Распределение ресурсов (ограничение - требования к качеству продукции, несколько периодов)
25 марта 2015 г.
- Группы статей
- Надстройка "Поиск решения"
Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). В качестве ограничения используем требования к качеству продукции. Расчет будем проводить с помощью надстройки Поиск решения.
Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты.
Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Задача
Компания владеет 4-мя карьерами, из которых она может добывать известняк различного качества. Особенно важны 2 характеристики: содержание в породе кальция и магния. Компания должна выполнить заказ на поставку известняка (в течение 5 лет). Продукция должна отгружаться ежегодно и должна содержать в среднем определенное количество кальция и магния на тонну. Годовые затраты на эксплуатацию каждого карьера фиксированы и составляют значительную величину. Каждый карьер имеет свою производительность. Суммарная мощность карьеров избыточна для выполнения заказа. По причине требований к защите окружающей среды в год возможна эксплуатация только 3-х или менее карьеров. Чтобы минимизировать затраты необходимо по каждому карьеру ежегодно принимать решение: эксплуатировать его в этом году или нет? (пример с сайта www.solver.com )
Примечание . Задача, в которой минимизируются затраты, понесенные в одном периоде решена в статье Поиск решения MS EXCEL (1.4). Распределение ресурсов (ограничение - требование к качеству продукции) , и имеет смысл предварительно познакомиться с изложенным там материалом.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).
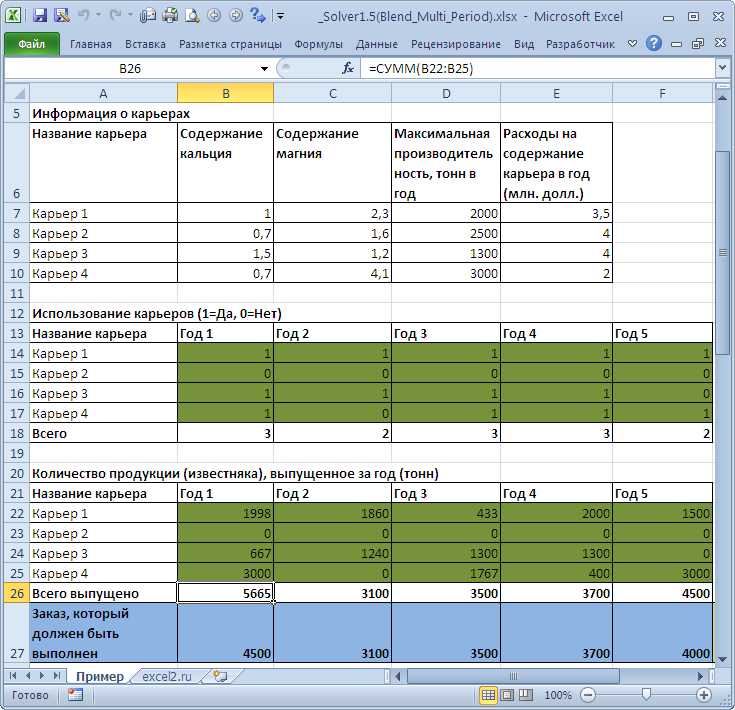
Переменные (выделено зеленым) . В качестве переменных модели следует взять бинарные значения (0 или 1), означающие 0 – карьер закрыт, 1 – открыт. Также необходимо варьировать количество известняка, выпускаемое каждым карьером, чтобы рассчитать содержание кальция и магния.
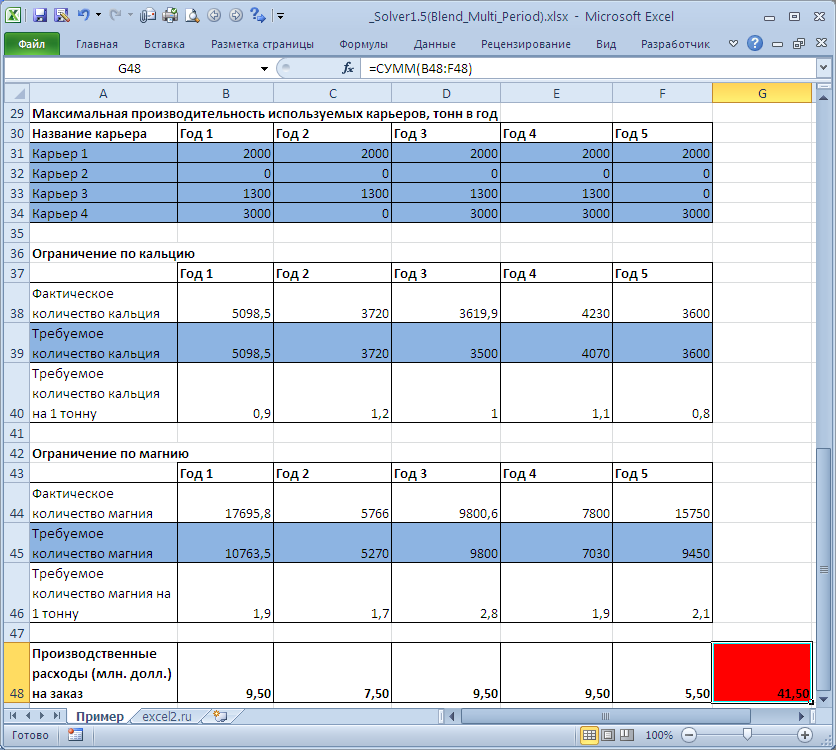
Ограничения (выделено синим) . Среднее содержание кальция и магния должно удовлетворять требования спецификации. Заказ должен быть выполнен. Объем выпущенной карьером продукции не должен превосходить его максимальной производительности.
Целевая функция (выделено красным) . Суммарные расходы за 5 лет на содержание открытых карьеров должны быть минимальны.
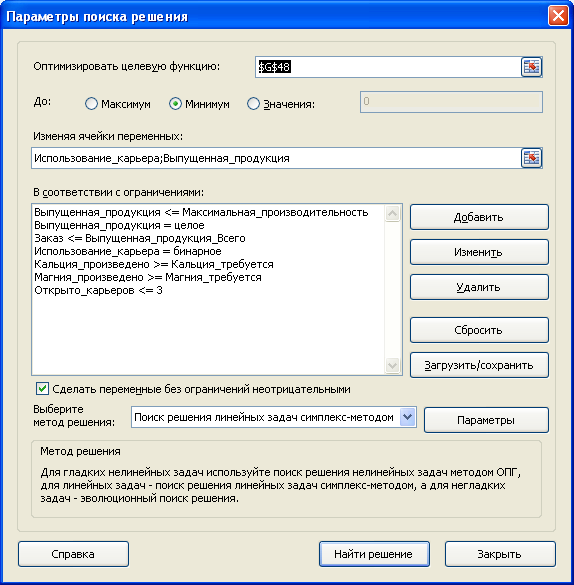
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .
Комментарии