Стандартная задача линейного программирования (ограничения на переменные выражены неравенствами) решена нами с помощью Поиска решения в предыдущей статье. Пример записи ограничений в такой задаче приведен ниже:

Как видно из картинки выше в задаче задано 3 ограничения (неравенства). Есть еще 4 ограничения (по числу переменных) - все переменные должны больше 0. 

Примечание: В стандартной задаче все переменные больше 0. На то она и стандартная.

В этой статье сведем стандартную задачу к каноническому виду и решим ее с помощью Поиска решения (Solver) в MS EXCEL.

Дадим определение.

Канонической называется задача линейного программирования, которая состоит в нахождении максимального или минимального значения целевой функции при условии, что все ограничения являются равенствами.

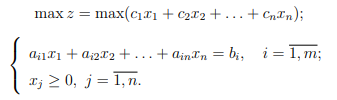
Примечание: Каноническая форма необходима для решения задачи симплекс методом (SIMPLEX LP).

Теперь задача.

Пусть требуется максимизировать целевую функцию F(x₁, x₂, x₃, x₄) = 2*x₁+3*x₂+x₃-5*x₄ 

Примечание: Ограничения задачи заданы выше.

Для приведения задачи к канонической форме введем дополнительные (свободные) переменные (т.е. произведем эквивалентные преобразования). Так как у нас три ограничения, то и дополнительных переменных должно быть 3. Введение этих переменных позволяет избавиться от неравенств в ограничениях и заменить их на равенства.

Совет: для знакомства с Поиском решения см. эту статью.

Решение

Сначала на лист EXCEL поместим все коэффициенты из 3-х неравенств (3х4) и добавим еще коэффициенты для 3-х свободных переменных (в форме единичной матрицы 3х3).

Также нужно заполнить столбец свободных членов (правая часть неравенств, синие ячейки).

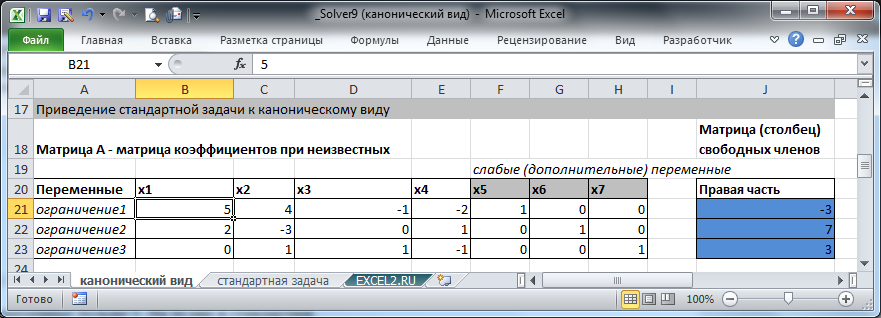
Теперь определим ячейки для хранения значений переменных х, выделим их зеленым цветом и расположим их в одном столбце (а не в строке). Значения этих ячеек Поиск решения будет изменять, чтобы максимизировать функцию F.

Напомним, что в задаче 4 переменных (x₁, x₂, x₃, x₄) и 3 дополнительных переменных (x₅, x₆, x₇), необходимых для сведения задачи к каноническому виду, поэтому нам потребовалось 7 ячеек.

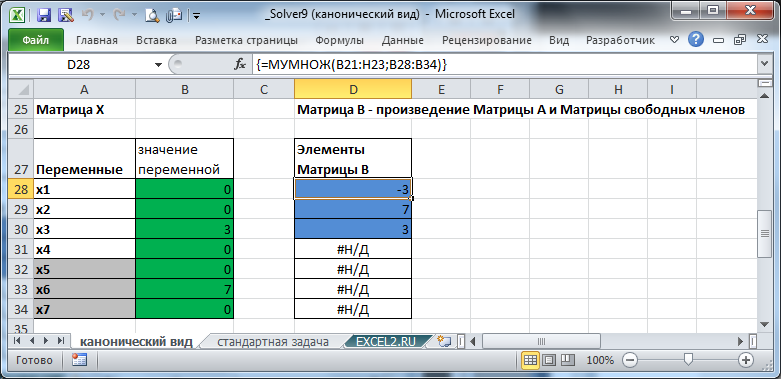
Теперь вычислим значения левых частей наших 3-х ограничений, то есть умножим коэффициенты Матрицы А на столбец переменных (Матрица Х, или просто столбец с переменными). Это можно сделать с помощью формулы =МУМНОЖ(B21:H23;B28:B34), т.е. использовав умножение матриц. Формулу нужно вводить как формулу массива, возвращающим сразу несколько значений.

Примечание. Альтернативным и интуитивно более понятным подходом является использование формулы =СУММПРОИЗВ(B21:H21;ТРАНСП($B$28:$B$34)) Это реализовано в файле примера. Формулу тоже нужно ввести как формулу массива, т.к. СУММПРОИЗВ() работает с массивами (векторами), которые оба размещены по строкам или по столбцам. В нашем случае это не так: коэффициенты размещены в одной строке, а значения х в столбце, поэтому использована функция ТРАНСП() для транспонирования столбца с переменными. Можно, конечно, предварительно транспонировать столбец в строку, в этом случае функцию СУММПРОИЗВ() можно вводить как обычную формулу.

Итак, у нас полностью сформировалось 3 ограничения: левая часть выражения (элементы Матрицы В) и правая часть (дано). Выделим эти ячейки синим цветом, чтобы было удобнее вводить условия в окно Поиска решения. Т.к. мы ввели дополнительные переменные, то ограничения теперь заданы в виде равенств - это канонический вид.

Осталось задать целевую функцию, умножив коэффициенты на ячейки с переменными (дополнительные переменные использовать не нужно). Это проще всего сделать формулой =СУММПРОИЗВ(B40:B43;B28:B31)

В окне Поиска решения задайте параметры оптимизации.

Совет: О том как установить Поиск решения  см. эту статью.

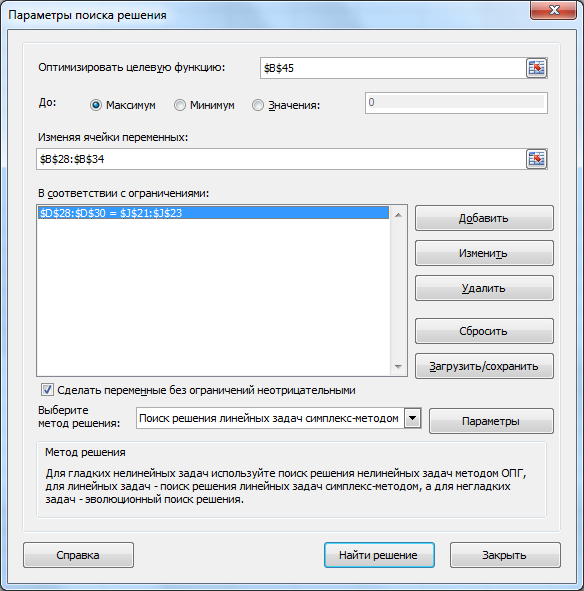
Поиск решения сам предложил решить задачу Симплекс-методом, а также сделать переменные неотрицательными.

После запуска Поиска решения решение будет найдено и оно, конечно, совпадет с решением задачи, которая была решена в стандартной форме.