Функция ПЛТ() в EXCEL

Функция ПЛТ( ) , английский вариант PMT(), позволяет рассчитать месячную сумму платежа по кредиту в случае аннуитетных платежей (когда за кредит платится равными частями).

Блок статей, посвященных теории и расчетам параметров аннуитета размещен здесь . В этой статье рассмотрены только синтаксис и примеры использования функции ПЛТ() .

Синтаксис функции ПЛТ()

ПЛТ(ставка; кпер; пс; [бс]; [тип])

• Ставка. Процентная ставка по кредиту (ссуде).
• Кпер. Общее число выплат по кредиту.
• пс. Сумма кредита.
• Бс. Необязательный аргумент. Требуемое значение остатка по кредиту после последнего платежа. Если этот аргумент опущен, предполагается, что он равен 0 (кредит будет полностью возвращен).
• Тип. Необязательный аргумент. Принимает значение 0 (нуль) или 1. Если =0 (или опущен), то принимается, что регулярный платеж осуществляется в конце периода, если 1, то в начале периода (сумма регулярного платежа будет несколько меньше).

Выплаты, возвращаемые функцией ПЛТ() , включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или комиссий, иногда связываемых со ссудой.

Пример 1

Предположим, человек планирует взять кредит в размере 50 000 руб. (ячейка В8 ) в банке под 14% годовых ( B6 ) на 24 месяца ( В7 ) (см. файле примера ).

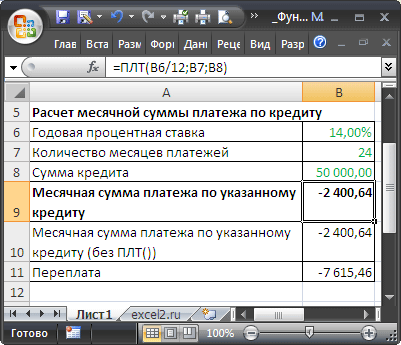
Расчет Месячной суммы платежа по такому кредиту с помощью функции ПЛТ()

=ПЛТ(B6/12;B7;B8)

СОВЕТ : Убедитесь, что Вы последовательны в выборе временных единиц измерения для задания аргументов "ставка" и "кпер". В нашем случае рассчитываются ежемесячные выплаты по двухгодичному займу (24 месяца ) из расчета 14 процентов годовых ( 14% / 12 месяцев ).

Расчет Месячной суммы платежа по такому кредиту с помощью БЕЗ функции ПЛТ()

=-B8*(B6/12*(1+B6/12)^B7)/((1+B6/12)^B7-1)

Для нахождения суммы переплаты, умножьте возвращаемое функцией ПЛТ() значение на "кпер" (получите число со знаком минус) и прибавьте сумму кредита. В нашем случае переплата составит 7 615,46 руб. (за 2 года).

Пример 2

Предположим, человек планирует ежемесячно откладывать деньги, чтобы скопить через 5 лет (ячейка E7 ) 1 млн. рублей ( E8 ). Деньги ежемесячно он планирует относить в банк и пополнять свой вклад. В банке действует процентная ставка 10% ( E6 ) и человек полагает, что она будет действовать без изменений в течение 5 лет. Какую сумму человек должен ежемесячно относить в банк, чтобы таким образом через 5 лет скопить 1 млн. руб.? (см. файле примера ).

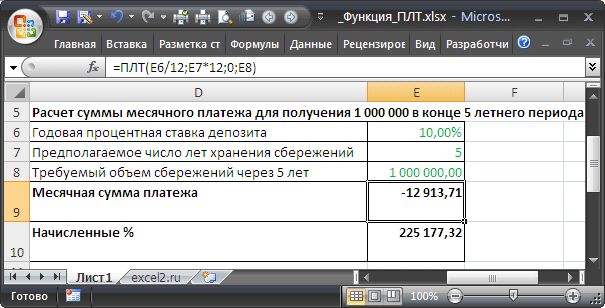
Расчет ежемесячной суммы платежа в таком случае можно также с помощью функции ПЛТ()

=ПЛТ(E6/12;E7*12;0;E8)

К концу 5 летнего периода сумма начисленных процентов составит более 225 тыс. руб., т.е. если бы человек просто складывал бы деньги себе в сейф, то он скопил бы только порядка 775 тыс. руб.