Сочетания без повторений: Комбинаторика в EXCEL
2 февраля 2016 г.
- Группы статей
- Комбинаторика
Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).
Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:
(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)
Примечание : Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье - плохая идея.
Отличие Сочетаний от Размещений
В отличие от Размещений следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор Сочетаний включается только одна из этих комбинаций. Очевидно, что для тех же n и k число Сочетаний всегда меньше чем число Размещений (так как при размещениях порядок важен, а для сочетаний - нет), причем в k! раз.
Подсчет количества Сочетаний
Число всех Сочетаний из n элементов по k можно вычислить по формуле:
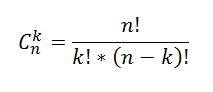
Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6} равно 15=6!/(4!(6-4)!)
Примечание
: Для
Сочетаний
из n элементов по k также используется и другая запись:
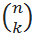
В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции - COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .
Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.
Примечание : О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье Сочетания с повторениями: Комбинаторика в MS EXCEL
Вывод всех комбинаций Сочетаний
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.
Задавая с помощью элементов управления Счетчик количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.
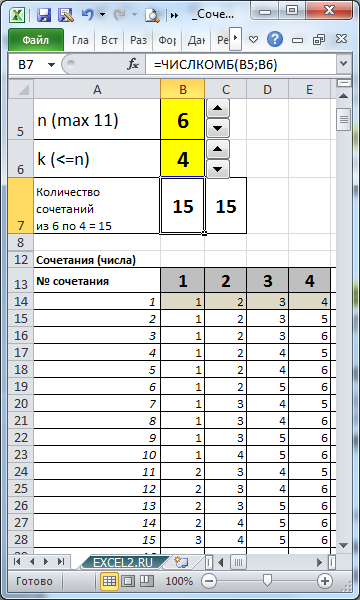
В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.
Задача
Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.
Нам нужно определить число Сочетаний 7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.
Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
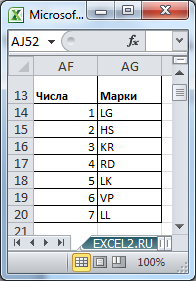
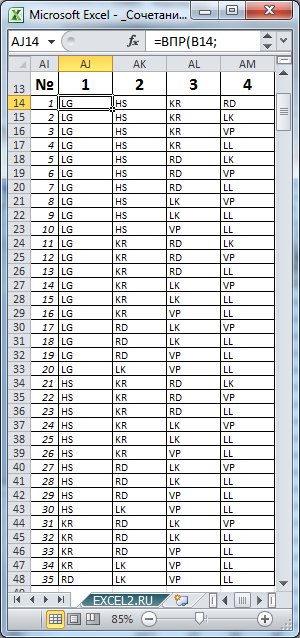
Выставив в ячейках В5 и В6 значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).
Примечание : О Перестановках можно прочитать в статье Перестановки без повторений: Комбинаторика в MS EXCEL , а о Размещениях в статье Размещения без повторений: Комбинаторика в MS EXCEL .
Комментарии