Оптимизация смен рабочих с помощью Поиска решений в EXCEL

Решим задачу об оптимизации смен рабочих с помощью Поиска решений MS EXCEL 2010. В качестве примера разберем задачу из сборника "Методы оптимизации управления и принятия решений" авторы Зайцев М.Г. и Варюхин С.Е. (2008г.). Задача 2.43 "Проблема мастера".

Сборник задач "Методы оптимизации управления и принятия решений" довольно популярен в качестве задачника для Вузов, поэтому ссылки на него встречаются повсеместно в интернете. Приятно, что для каждой задачи имеется ответ в конце книги - можно сравнить получившееся решение с решением, которое найдено авторами с помощью Поиска решения (в году так 2000-м, я полагаю).

Условия задачи (оригинальные)

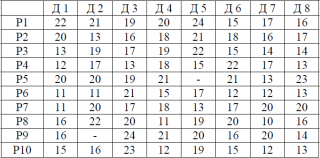
Мастер должен выбрать несколько фрезеровщиков из 10 (Р1,Р2..Р10) для изготовления 8 видов деталей (Д1,Д2,...Д8) для партии продукции:

так, чтобы сократить общие затраты рабочего времени. Среднее количество деталей, которое каждый рабочий может обработать за смену, дано в таблице:

а. Определить оптимальное распределение рабочих по операциям, принимая во внимание, что рабочие Р5 и Р9 не могут изготавливать детали Д5 и Д2 соответственно.b. Каков самый короткий срок выполнения этого заказа?

Разбор условия задачи

Скажу честно, но условия задачи не кажутся мне четко сформулированными. Вот мои комментарии:

1) Рабочих называют сначала фрезеровщиками, затем просто рабочими. Зачем?

2) Используется понятие "операции", то есть подразумевается некая определенная последовательность действий. То есть можно подумать, что сначала делается операция Д1 (изготовление детали 1), затем Д2 и т.д. Чтобы выяснить это, обратимся к ответу:

То есть нет никаких последовательных операций, есть просто 8 типов деталей, которые нужно изготовить. Причем один рабочий изготавливает за смену или дольше только один вид деталей, затем, если есть необходимость, то переходит к другому типу. Понятие "операции" не помогает студенту понять условие, а лишь его запутывает.

3) В ответе целая и дробные части смены отделены точкой, но как известно, в России разделителем является запятая. Кроме того, очевидно, что дробная часть смены приведет к дробному количеству изготовленных деталей (это как то непонятно). Как следствие, в задаче планируется складывать 63,111 и 48,888 деталей, чтобы выполнить заказ. Что не очень логично.

4) В условии используется " среднее количество деталей, которое каждый рабочий может обработать за смену". Как будто, эту задачу планируется решать статистическими методами с использованием некой функции распределения.

5) Зачем сказано, что "рабочие Р5 и Р9 не могут изготавливать детали Д5 и Д2"? Просто поставьте ноль, никакого смысла в этом условии нет.

Кроме безобидных неточностей в формулировках условия в формулировке задачи отсутствуют 2 дополнительных ограничений, без которых вышеуказанный ответ не получить. Разберемся в этом, решив задачу.

Решение

Если вы не знакомы с Поиском решения, то для начала прочитайте статью Поиск решения MS EXCEL. Знакомство .

Чтобы построить модель для Поиска решения (ПР) в EXCEL нужно определить 3 ее составляющих:

• целевая функция (то, что мы будем оптимизировать, например, минимизировать трудозатраты), это формула в одной ячейке ( ячейку выделим красным );
• переменные модели, это то что будет изменять ПР в ходе поиска ( ячейки выделим зеленым );
• ограничения модели, например, Заказ должен быть выполнен ( ячейки выделим синим ).

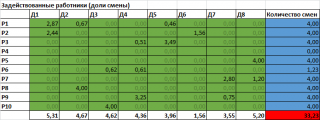
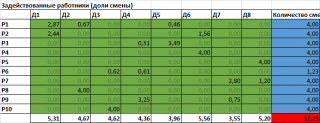
Создадим в файле примера на листе а вспомогательную таблицу (загрузка рабочих по сменам) и заполним ее данными из вышеуказанного решения.

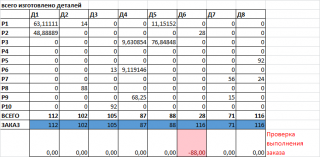
Теперь рассчитаем, сколько же деталей будет изготовлено при такой загрузке рабочих.

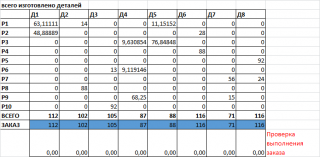
Оказывается, в решении опечатка. При данном ответе не будет выполнен заказ - основное условие задачи. Оказывается, деталь Д6 также изготавливает рабочий Р4. После добавления нужного количества смен, получим правильный ответ - теперь заказ выполнен.

Вернемся к таблице загрузки рабочих по сменам и еще раз внимательно посмотрим на решение, приведенное в задачнике.

Оказывается, количество смен у каждого рабочего составляет от 1 до 4 (ровно)! Почему? Потому что, это дополнительное ограничение, про которое ничего не сказано в условии задачи. Получим это решение. Для этого создадим модель.

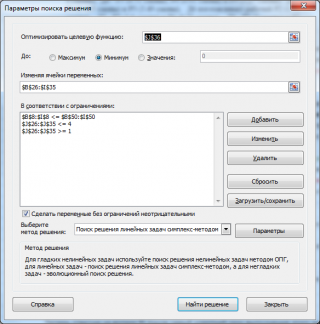
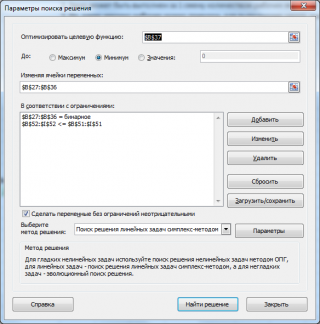
Будем минимизировать общее количество смен всех рабочих (см. формулу в красной ячейке). В качестве ограничений потребуем выполнение заказа и загрузку каждого рабочего от 1 до 4 смен. Переменными являются ячейки, содержащие количества смен рабочих.

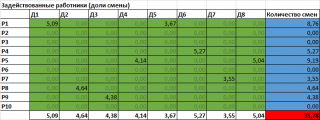
Нажав кнопку Найти решение получим именно тот ответ, который дан в задачнике. Чтобы понять, откуда взялось ограничение про загрузку каждого рабочего от 1 до 4 смен, удалим эти ограничения и снова запустим Поиск решения. Вот ответ:

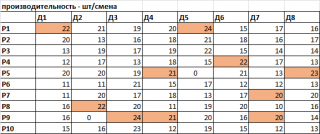
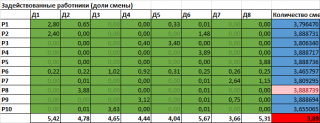
Как видим, общее количество смен всех рабочих уменьшилось (35,78 против 37,23). Так зачем авторам потребовались эти дополнительные ограничения? Дело в том, что без этих ограничений мы получим тривиальный ответ, который очевиден и без Поиска решения! Сравните загрузку рабочих с их производительностью:

Максимальная производительность выделена цветом и поразительно совпадает с найденным решением. На самом деле решение очевидно: чтобы сократить загрузку рабочих - возьми самых производительных (по типам деталей) и загрузи их! Этот факт приводит к мысли, что либо задача некорректно сформулирована, либо неправильно решена. Будем грешить на решение.

Перед тем как решить  задачу другим способом, ответим на второй вопрос задачи: "Каков самый короткий срок выполнения этого заказа?" (см. файл примера, лист б )

Чтобы вычислить самый короткий срок выполнения заказа - просто уберем 2 доп. ограничения о количестве смен (от 1 до 4) в окне Поиска решения и изменим целевую функцию в красной ячейке J31 . Теперь будем МИНимизировать МАКСимальную длительность смен рабочих ( =МАКС(J21:J30) ).

При этом считаем, что все 10 рабочих работают независимо друг от друга (на разных станках), поэтому время выполнения заказа будет равно максимальному количеству смен у одного из рабочих. Полученный ответ 3,89 совпадает с ответом в задачнике (менее 4-х дней).

Альтернативное решение

Теперь попробуем переформулировать условие задачи.

Во-первых, предположим, что каждый рабочий за 8-ми часовую смену обязан сделать все 8 типов деталей (от Д1 до Д8). Т.е., в 1-й час каждый рабочий делает Д1, во 2-й час каждый рабочий делает Д2 и т.д. Производительность дана в таблице.

Во-вторых, заказ нужно сделать за 1 смену.

Вопрос: каких рабочих нужно взять, чтобы выполнить заказ минимальным количеством рабочих?

При такой формулировке задачи мы избавляемся от нецелых смен и дробных деталей (каждый рабочий работает 1 смену). Также мы не получаем тривиального решения.

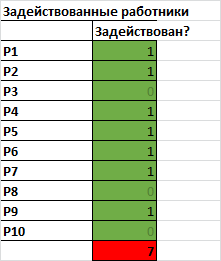
Если для выполнения заказа мы берем рабочего, то ему присваивается значение 1, если нет, то 0.

Поиск решения (по прежнему линейная задача) находит, что достаточно взять 7 рабочих, чтобы выполнить заказ. В этом случае, правда, заказ будет несколько перевыполнен по некоторым типам деталей.

Также можно усложнить задачу, вычислив, каких именно рабочих требуется взять, чтобы излишки по заказу были минимальны.