Поиск решения EXCEL (1.1). Оптимальная структура выпускаемой продукции

Создадим модель для определения Оптимальной структуры выпускаемой продукции (Product Mix), при котором выручка максимальна. Расчет будем проводить с помощью надстройки Поиск решения. За основу возьмем пример из файла solvsamp.xls, поставляемый с MS EXCEL.

Рассмотрим задачу определения Оптимальной структуры выпускаемой продукции (Product Mix) на основе примера из файла solvsamp.xls (при установленном MS EXCEL 2010 файл находится в папке C:\Program Files\Microsoft Office\Office14\SAMPLES).

Совет . Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .

Задача

Предприятие выпускает 3 вида изделий: телевизоры, стерео системы и динамики. Все 3 изделия собираются, используя общий набор комплектующих: рама, кинескоп, кинескоп, динамик, блок питания и электронная плата, количество которых ограничено запасом на складе. Необходимо найти соотношение объемов выпуска изделий, при котором общий доход от их продажи максимален (другими словами: из имеющихся на складе комплектующих необходимо изготовить такой набор изделий, доход от продажи которого максимален).

Создание модели

На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).

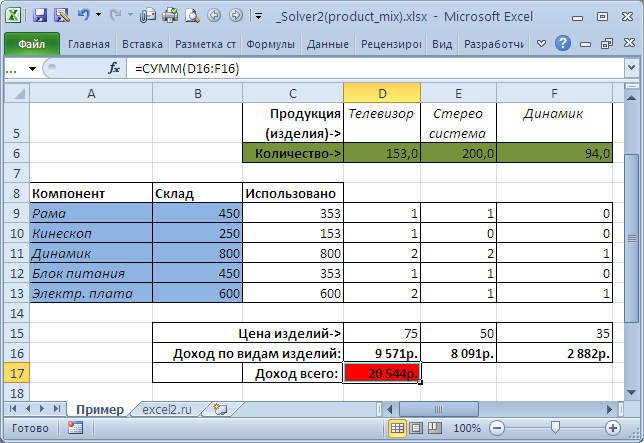
Переменные . Очевидно, что в качестве переменных модели следует определить объемы выпуска каждого из изделий (количество). Соответствующие ячейки выделены зеленым. Целевая функция . Целевая функция – это формула, рассчитывающая совокупный доход от продажи всех изделий (выделено красным). Доход от каждого изделия считается как произведение цены изделия на его количество. Величина дохода содержит еще один множитель, который зависит от количества изделия. Поясним его предназначение. В модели предполагается, что удельный доход от каждой последующей продажи изделия - уменьшается (например, в связи с дополнительными затратами на сбыт). Это реализовано с помощью множителя (на основе логарифма) монотонно убывающего с ростом количества изделий, что, кстати, делает модель нелинейной.

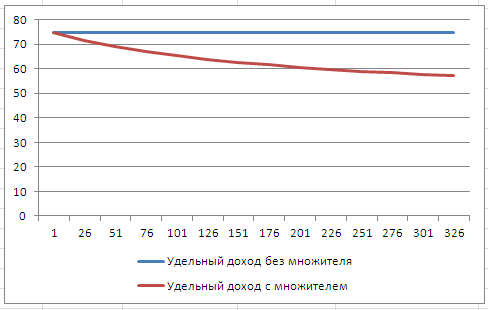
Множитель требуется, чтобы решение задачи при данном соотношении цен не было тривиальным (в противном случае решить задачу можно без привлечения Поиска решения : собрать сначала из имеющихся на складе комплектующих максимально возможное  количество самых дорогих изделий (ТВ), затем подешевле (Стерео), а из остатков – самое дешевое изделие). Из-за этого множителя, при определенном количестве дорого изделия, становится выгоднее собирать изначально более дешевые изделия, что делает задачу интереснее.

Ограничения . Ограничения модели также понятны – количество изделий должно быть целым, а количество использованных комплектующих не должно превышать имеющихся на складе.

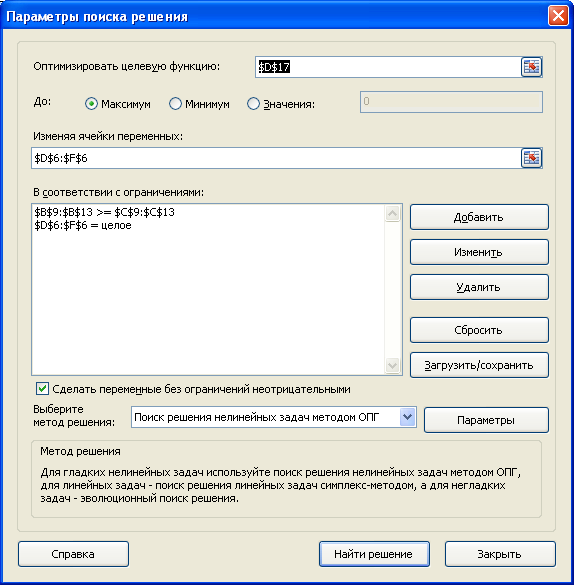
Убедитесь, что метод решения соответствует нелинейной задаче. Теперь в диалоговом окне можно нажать кнопку Найти решение .

Результаты расчетов

Поиск решения нашел оптимальное решение: при изготовлении 153 ТВ, 200 Стерео систем и 94 Аудио систем величина суммарного дохода максимальна и равна 20544,39. Простота рассмотренной модели является причиной ее ограничений:

• модель не учитывает величины рыночного спроса (предполагается, что мы продадим все изделия);
• оптимизируется лишь доход, но не прибыль, т.к. не учитывается стоимость комплектующих (например, при определенном количестве производство телевизоров может стать убыточным из-за снижения удельной цены).

Примечание . В статье Поиск решения MS EXCEL (1.2). Распределение ресурсов (ограничение по количеству оборудования) решим задачу определения наилучшего распределения ресурсов, при котором минимизируются затраты (Allocation Problem). Примечание . В статье Поиск решения MS EXCEL (1.1a). Оптимальная структура выпускаемой продукции (с приобретением недостающего объема продукции) решим задачу определения структуры производства в случае недостаточного объема материалов.