Уровень значимости и уровень надежности в EXCEL

Дадим определение терминам уровень надежности и уровень значимости. Покажем, как и где они используется в MS EXCEL .

Уровень значимости (Level of significance) используется в процедуре проверки гипотез и при построении доверительных интервалов .

СОВЕТ : Для понимания терминов Уровень значимости и Уровень надежности потребуется знание следующих понятий:

• выборочное распределение среднего ;
• стандартное отклонение ;
• проверка гипотез ;
• нормальное распределение .

Уровень значимости статистического теста – это вероятность отклонить нулевую гипотезу , когда на самом деле она верна. Другими словами, это допустимая для данной задачи вероятность ошибки первого рода (type I error).

Уровень значимости обычно обозначают греческой буквой α ( альфа ). Чаще всего для уровня значимости используют значения 0,001; 0,01; 0,05; 0,10.

Например, при построении доверительного интервала для оценки среднего значения распределения , его ширину рассчитывают таким образом, чтобы вероятность события « выборочное среднее (Х _ср ) находится за пределами доверительного интервала » было равно уровню значимости . Реализация этого события считается маловероятным (практически невозможным) и служит основанием для отклонения нулевой гипотезы о равенстве среднего заданному значению .

Ошибка первого рода часто называется риском производителя. Это осознанный риск, на который идет производитель продукции, т.к. он определяет вероятность того, что годная продукция может быть забракована, хотя на самом деле она таковой не является. Величина ошибки первого рода задается перед проверкой гипотезы , таким образом, она контролируется исследователем напрямую и может быть задана в соответствии с условиями решаемой задачи.

Чрезмерное уменьшение уровня значимости α (т.е. вероятности ошибки первого рода ) может привести к увеличению вероятности ошибки второго рода , то есть вероятности принять нулевую гипотезу , когда на самом деле она не верна. Подробнее об ошибке второго рода см. статью Ошибка второго рода и Кривая оперативной характеристики .

Уровень значимости обычно указывается в аргументах обратных функций MS EXCEL для вычисления квантилей соответствующего распределения: НОРМ.СТ.ОБР() , ХИ2.ОБР() , СТЬЮДЕНТ.ОБР() и др. Примеры использования этих функций приведены в статьях про проверку гипотез и про построение доверительных интервалов .

Уровень надежности

Уровень доверия (этот термин более распространен в отечественной литературе, чем Уровень надежности ) - означает вероятность того, что доверительный интервал содержит истинное значение оцениваемого параметра распределения.

Уровень доверия равен 1-α, где α – уровень значимости .

Термин Уровень надежности имеет синонимы: уровень доверия, коэффициент доверия, доверительный уровень и доверительная вероятность (англ. Confidence Level , Confidence Coefficient ).

В математической статистике обычно используют значения уровня доверия 90%; 95%; 99%, реже 99,9% и т.д.

Например, Уровень доверия 95% означает, что событие, вероятность которого 1-0,95=5% исследователь считать маловероятным или невозможным. Разумеется, выбор уровня доверия полностью зависит от исследователя. Так, степень доверия авиапассажира к надежности самолета, несомненно, должна быть выше степени доверия покупателя к надежности электрической лампочки.

Примечание : Стоит отметить, что математически не корректно говорить, что Уровень доверия является вероятностью, того что оцениваемый параметр распределения принадлежит доверительному интервалу , вычисленному на основе выборки . Поскольку, считается, что в математической статистике отсутствуют априорные сведения о параметре распределения. Математически правильно говорить, что доверительный интервал , с вероятностью равной Уровню доверия, накроет истинное значение оцениваемого параметра распределения.

Уровень надежности в MS EXCEL

В MS EXCEL Уровень надежности упоминается в надстройке Пакет анализа . После вызова надстройки, в диалоговом окне необходимо выбрать инструмент Описательная статистика .

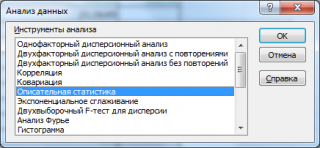
После нажатия кнопки ОК будет выведено другое диалоговое окно.

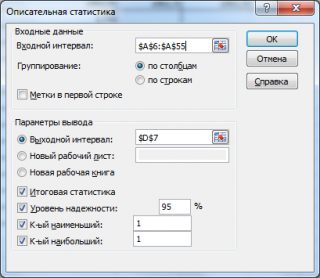
В этом окне задается Уровень надежности, т.е.значениевероятности в процентах. После нажатия кнопки ОК в выходном интервале выводится значение равное половине ширины доверительного интервала . Этот доверительный интервал используется для оценки среднего значения распределения, когда дисперсия не известна (подробнее см. статью про доверительный интервал ).

Необходимо учитывать, что данный доверительный интервал рассчитывается при условии, что выборка берется из нормального распределения . Но, на практике обычно принимается, что при достаточно большой выборке (n>30), доверительный интервал будет построен приблизительно правильно и для распределения, не являющегося нормальным (если при этом это распределение не будет иметь сильной асимметрии ).

Примечание : Понять, что в диалоговом окне речь идет именно об оценке среднего значения распределения , достаточно сложно. Хотя в английской версии диалогового окна это указано прямо: Confidence Level for Mean .

Если Уровень надежности задан 95%, то надстройка Пакет анализа использует следующую формулу (выводится не сама формула, а лишь ее результат):

=СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) *СТЬЮДЕНТ.ОБР.2Х(1-0,95;СЧЁТ(Выборка)-1)

или эквивалентную ей

=СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) *СТЬЮДЕНТ.ОБР((1+0,95)/2;СЧЁТ(Выборка)-1)

где =СТАНДОТКЛОН.В(Выборка)/КОРЕНЬ(СЧЁТ(Выборка)) – является стандартной ошибкой среднего (формулы приведены в файле примера ).

или

=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95; СТАНДОТКЛОН.В(Выборка); СЧЁТ(Выборка))

Подробнее см. в статьях про доверительный интервал .