Равномерное непрерывное распределение в EXCEL

Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL СЛЧИС() и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.

Равномерно распределенная на отрезке [a; b] случайная величина имеет плотность распределения (вероятности) :

Функция распределения определяется следующим образом:

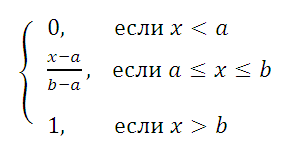
Равномерное непрерывное распределение (англ. Continuous uniform d istribution или Rectangular distribution ) часто встречается на практике.

Пример1. Например, известно, что гейзер извергается каждые 50 минут. Найти вероятность, того что турист увидит извержение, если будет ждать у гейзера 20 минут. В соответствии с вышеуказанными формулами вероятность увидеть извержение в течение времени наблюдения равна 20/50=0,4, т.е. 40%.

Пример2. Симметричный волчок после раскручивания падает набок. Вертикальная ось волчка после падения указывает на определенный угол от 0 до 360 градусов. Найти вероятность, того что ось волчка укажет на сектор от 90 до 180 градусов. Вероятность равна (180-90)/(360-0)=0,25.

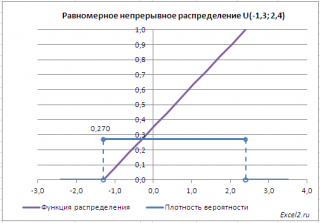
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .

Математическое ожидание и дисперсия

Математическое ожидание для равномерного непрерывного распределения вычисляется по формуле =(a+b)/2.

Дисперсия (квадрат стандартного отклонения) вычисляется по формуле =((b-a)^2)/12.

Генерация случайных чисел

Случайные числа, имеющие равномерное непрерывное распределение на отрезке [0; 1), можно сгенерировать с помощью функции MS EXCEL СЛЧИС() . В функции нельзя задать нижнюю и верхнюю границу интервала, но записав формулу =СЛЧИС()*(b-a)+a можно сгенерировать равномерно распределенные числа на любом интервале [a; b).

Примечание : Чтобы сгенерировать случайные числа, имеющие равномерное дискретное распределение , воспользуйтесь функцией СЛУЧМЕЖДУ() .

Сгенерировать случайные числа, извлеченные из непрерывного равномерного распределения, можно также с помощью надстройки Пакет анализа .

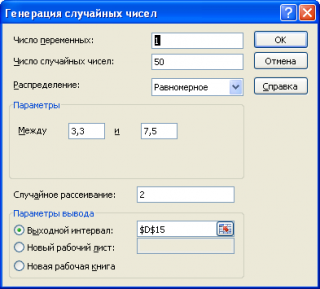
Сгенерируем массив из 50 чисел из диапазона [3,3; 7,5). Для этого в окне Генерация случайных чисел установим следующие параметры (см. файл примера лист Генерация ):

Как видно из рисунка выше, в поле Случайное рассеивание установлен необязательный параметр равный 2. Параметр Случайное рассеивание может принимать значение от 1 до 32767. Если установить этот параметр, то MS EXCEL будет каждый раз генерировать один и тот же массив чисел, соответствующий этот значению. Этот подход удобен для генерации одинаковых массивов, например, на различных компьютерах.

Оценка среднего и стандартного отклонения

Нижнюю и верхнюю границу интервала возьмем [3,3; 7,5) и разместим их в ячейках B4:B5 . Сгенерируем 50 чисел ( выборку ) и поместим их в диапазоне С14:С63 .

Математическое ожидание этого распределения =(B4+B5)/2 и равно 5,4. Стандартное отклонение распределения равно =КОРЕНЬ(((B5-B4)^2)/12)=1,21

Чтобы оценить математическое ожидание воспользуемся значениями выборки =СУММ(C14:C63)/СЧЁТ(C14:C63) .

Оценить стандартное отклонение можно с помощью формулы =СТАНДОТКЛОН.В(C14:C63) в MS EXCEL 2010 или =СТАНДОТКЛОН(C14:C63) для более ранних версий.

Чтобы оценить дисперсию используйте формулу =ДИСП.В(C14:C63) в MS EXCEL 2010 или =ДИСП(C14:C63) для более ранних версий. Также можно использовать формулу =СТАНДОТКЛОН.В(C14:C63)^2 .

СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .