Распределение Вейбулла. Непрерывные распределения в EXCEL

Рассмотрим распределение Вейбулла, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ВЕЙБУЛЛ.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров распределения.

Распределение Вейбулла (англ. Weibull distribution ) зависит от 2-х параметров: α ( альфа)>0 (определяет форму распределения) и b ( бета)>0 (определяет масштаб). Плотность вероятности этого распределения задается следующей формулой:

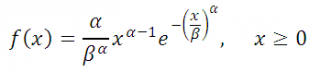
Если параметр альфа = 1, то распределение Вейбулла превращается в экспоненциальное распределение . Параметр бета на практике обычно принимается >=1.

Функция распределения задается следующей формулой:

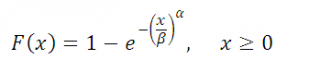
СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .

Математическое ожидание и дисперсия распределения задаются следующими выражениями:

где Г(r) – гамма-функция:

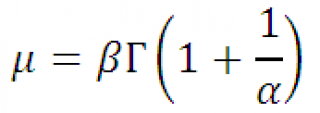
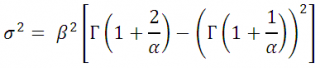
если r – положительное целое, то Г(r)=(r-1)!

Распределение Вейбулла является адекватной моделью для описания времени безотказной работы многих технических устройств:

• время отказа вследствие износа (wearout failure time). Отказ должен происходить из-за поломки наименее надежного комплектующего (weakest link principle);
• время отказа материала по причине разрушения (material strength). Отказ должен происходить по причине наличия внутреннего дефекта. Если параметр альфа = 1 ( экспоненциальное распределение ), то причиной отказа должна служить внешняя причина.

Распределение Вейбулла в MS EXCEL

В MS EXCEL, начиная с версии 2010, для распределения Вейбулла имеется функция ВЕЙБУЛЛ.РАСП() , английское название - WEIBULL.DIST(), которая позволяет вычислить плотность вероятности и интегральную функцию распределения (вероятность, что случайная величина X, имеющая распределение Вейбулла , примет значение меньше или равное x).

Примечание : До MS EXCEL 2010 в EXCEL была функция ВЕЙБУЛЛ() , которая позволяет вычислить интегральную функцию распределения и плотность вероятности . ВЕЙБУЛЛ() оставлена в MS EXCEL 2010 для совместимости.

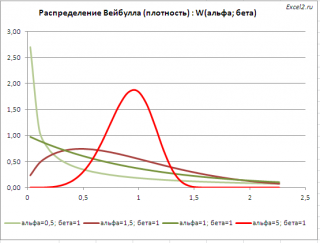
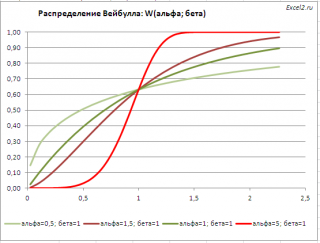
Графики функций

В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения при нескольких параметрах альфа и бета .

Распределение Вейбулла имеет обозначение Weibull (альфа; бета) или просто W (альфа; бета).

Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .

Примечание : Для удобства написания формул в файле примера для параметров распределения альфа и бета созданы соответствующие Имена .

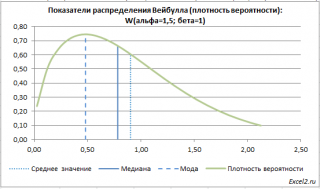
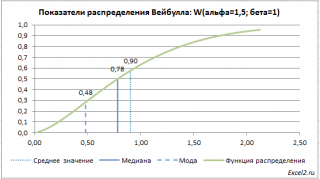
В файле примера также построены графики плотности вероятности и функции распределения с отмеченными значениями среднего , медианы и моды .

Генерация случайных чисел и оценка параметров

Используем обратную функцию распределения (или p - quantile , см. статью про Квантили ), которая для распределения Вейбулла может быть выражена в явном виде с использованием элементарных функций:

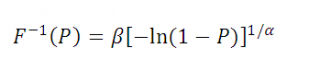
С помощью этой функции можно сгенерировать значения случайной величины, имеющей распределение Вейбулла . Для этого нужно использовать формулу MS EXCEL:

=бета*(-LN(СЛЧИС()))^(1/альфа)

Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).

Теперь имея массив случайных чисел, сгенерированных с заданными параметрами распределения альфа и бета (пусть их будет 200), оценим параметры распределения.

Оценку параметров альфа и бета можно сделать с помощью линейной регрессии. Для этого необходимо привести функцию распределения Вейбулла к виду обычной прямой, задаваемой уравнением Y=aX+b. Для этого сделаем следующие преобразования:

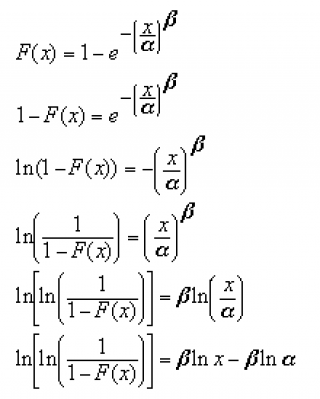
Сравнивая выражение с уравнением прямой Y=ax+b получим, что:

• Y соответствует левая часть выражения,
• X – соответствует ln(x),
• параметр распределения бета соответствует коэффициенту a , отвечающего за наклон прямой к оси абсцисс.
• выражение –бета*ln(альфа) соответствует коэффициенту b (ордината точки пересечения с осью Oy).

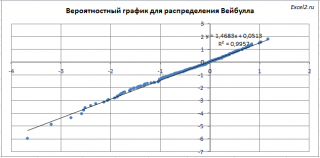
По сути, мы практически построили Вероятностный график (probability plot) для распределения Вейбулла : если отсортированные значения ln(x), отложенные по оси Ох, лягут приблизительно вдоль прямой, то это будет означать, что значения выборки взяты из распределения Вейбулла. Осталось модифицировать ось Оу с помощью формулы =LN(-LN(1-Ui)), где Ui=(i-0,5)/200, а i=1; 2; ...; 200.

Заметим, что -LN(1-Ui) – это обратная функция распределения с параметрами альфа=1 и бета=1. Второй логарифм нам потребовался, т.к. по оси абсцисс отложены не сами x, а ln(x).

Примечание : Т.к. форма распределения Вейбулла существенно зависит от его параметров, то вместо альфа=1 и бета=1 для обратной функции лучше использовать точечные оценки этих параметров , полученные на основании выборки . О том как вычислить оценку параметров альфа и бета см. ниже.

В файле примера на листе Генерация построен соответствующий Вероятностный график .

С помощью функции НАКЛОН() вычислим наклон получившейся кривой (коэффициент прямой а, англ. slope ), который служит оценкой параметра бета .

Функция ОТРЕЗОК() вернет ординату точки пересечения с Оу (коэффициент прямой b ). Выражение =EXP(-b/бета) служит оценкой параметра альфа .

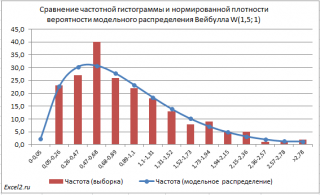
Построив частотную гистограмму по данным из выборки , сравним ее с плотностью вероятности модельного распределения, т.е. распределения, с помощью которого были сгенерированы сами значения выборки . Из-за наличия случайной ошибки выборки (sampling error) значения могут расходиться.

Процедура построения модельного распределения следующая:

• Значения плотности вероятности модельного распределения вычислены как P _i - P _i-1 , где P – значения интегральной функции распределения на границах интервалов гистограммы, а dx =1. (Обычно, плотность вероятности непрерывного распределения вычисляется как производная функции распределения dP/dx).
• Вследствие такого преобразования, мы перешли от непрерывного распределения к дискретному . Необходимо убедиться, что сумма плотностей вероятностей равна 1.
• Пронормировав модифицированные плотности вероятностей на количество значений в выборке (200), вычислим для каждого интервала частоты модельного распределения (можно обойтись без нормирования, использовав вспомогательную ось диаграммы).

В итоге получим:

Как видно из диаграммы выше, совпадение модельного распределения с гистограммой выборки достаточно хорошее.

Примечание : При построении диаграммы использована гистограмма и график с маркерами . Подробнее о построении диаграмм см. Основы построения диаграмм в MS EXCEL .

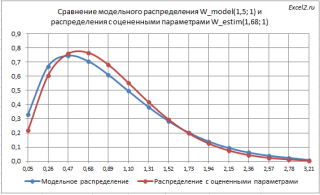
Также можно сравнить плотности вероятностей модельного распределения и распределения с параметрами, полученными в результате оценки.

Как видно из диаграммы выше, совпадение также достаточно хорошее.

СОВЕТ : Т.к. генерирование случайных чисел происходит с помощью функции СЛЧИС() , то нажимая клавишу F9 , можно каждый раз получать новую выборку и, соответственно, новую оценку параметров.

СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .