Распределение Пуассона. Дискретные распределения в EXCEL

Рассмотрим распределение Пуассона, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL ПУАССОН.РАСП() построим графики функции распределения и плотности вероятности. Произведем оценку параметра распределения, его математического ожидания и стандартного отклонения.

Сначала дадим сухое формальное определение распределения, затем приведем примеры ситуаций, когда распределение Пуассона (англ. Poisson distribution ) является адекватной моделью для описания случайной величины.

Если случайные события происходят в заданный период времени (или в определенном объеме вещества) со средней частотой λ( лямбда ), то число событий x , произошедших за этот период времени, будет иметь распределение Пуассона .

Плотность вероятности распределения Пуассона задается следующей формулой:

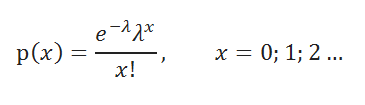
λ – единственный параметр распределения Пуассона .

СОВЕТ : подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .

Применение распределения Пуассона

Примеры, когда Распределение Пуассона является адекватной моделью:

• число вызовов, поступивших на телефонную станцию за определенный период времени;
• число частиц, подвергнувшихся радиоактивному распаду за определенный период времени;
• число дефектов в куске ткани фиксированной длины.

Распределение Пуассона является адекватной моделью, если выполняются следующие условия:

• события происходят независимо друг от друга, т.е. вероятность последующего события не зависит от предыдущего;
• средняя частота событий постоянна. Как следствие, вероятность события пропорциональна длине интервала наблюдения;
• два события не могут произойти одновременно;
• число событий должно принимать значения 0; 1; 2…

Примечание : Хорошей подсказкой, что наблюдаемая случайная величина имеет распределение Пуассона, является тот факт, что среднее значение выборки приблизительно равно дисперсии (см. ниже).

Ниже представлены примеры ситуаций, когда Распределение Пуассона не может быть применено:

• число студентов, которые выходят из университета в течение часа (т.к. средний поток студентов не постоянен: во время занятий студентов мало, а в перерыве между занятиями число студентов резко возрастает);
• число землетрясений амплитудой 5 баллов в год в Калифорнии (т.к. одно землетрясение может вызвать повторные толчки сходной амплитуды – события не независимы);
• число дней, которые пациенты проводят в отделении интенсивной терапии (т.к. число дней, которое пациенты проводят в отделении интенсивной терапии всегда больше 0).

Примечание : Распределение Пуассона является приближением более точных дискретных распределений: Гипергеометрического и Биномиального .

Примечание : О взаимосвязи распределения Пуассона и Биномиального распределения можно прочитать в статье Взаимосвязь некоторых распределений в MS EXCEL . О взаимосвязи распределения Пуассона и Экспоненциального распределения можно прочитать в статье про Экспоненциальное распределение .

Распределение Пуассона в MS EXCEL

В MS EXCEL, начиная с версии 2010, для Распределения Пуассона имеется функция ПУАССОН.РАСП() , английское название - POISSON.DIST(), которая позволяет вычислить не только вероятность того, что за заданный период времени произойдет х событий (функцию плотности вероятности p(x), см. формулу выше), но и интегральную функцию распределения (вероятность того, что за заданный период времени произойдет не меньше x событий).

До MS EXCEL 2010 в EXCEL была функция ПУАССОН() , которая также позволяет вычислить функцию распределения и плотность вероятности p(x). ПУАССОН() оставлена в MS EXCEL 2010 для совместимости.

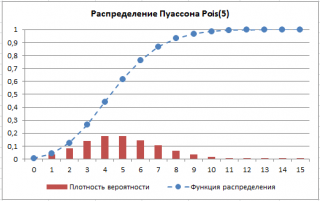
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .

Распределение Пуассона имеет скошенную форму (длинный хвост справа у функции вероятности), но при увеличении параметра λ становится все более симметричным.

Примечание : Для построения интегральной функции распределения идеально подходит диаграмма типа График , для плотности распределения – Гистограмма с группировкой . Подробнее о построении диаграмм читайте статью Основные типы диаграмм .

Примечание : Среднее и дисперсия (квадрат стандартного отклонения ) равны параметру распределения Пуассона – λ (см. файл примера лист Пример ).

Задача

Типичным применением Распределения Пуассона в контроле качества является модель количества дефектов, которые могут появиться в приборе или устройстве.

Например, при среднем количестве дефектов в микросхеме λ (лямбда) равном 4, вероятность, что случайно выбранная микросхема будет иметь 2 или меньше дефектов, равна: = ПУАССОН.РАСП(2;4;ИСТИНА)=0,2381

Третий параметр в функции установлен = ИСТИНА, поэтому функция вернет интегральную функцию распределения , то есть вероятность того, что число случайных событий окажется в диапазоне от 0 до 4 включительно.

Вычисления в этом случае производятся по формуле:

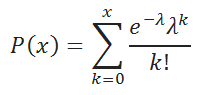
Вероятность того, что случайно выбранная микросхема будет иметь ровно 2 дефекта, равна: = ПУАССОН.РАСП(2;4;ЛОЖЬ)=0,1465

Третий параметр в функции установлен = ЛОЖЬ, поэтому функция вернет плотность вероятности.

Вероятность того, что случайно выбранная микросхема будет иметь больше 2-х дефектов, равна: =1-ПУАССОН.РАСП(2;4;ИСТИНА) =0,8535

Примечание : Если x не является целым числом, то при вычислении формулы дробная часть числа отбрасывается . Формулы =ПУАССОН.РАСП( 2 ; 4; ЛОЖЬ) и =ПУАССОН.РАСП( 2,9 ; 4; ЛОЖЬ) вернут одинаковый результат.

Генерация случайных чисел и оценка λ

С помощью надстройки Пакет анализа можно сгенерировать случайные числа, извлеченные из распределения Пуассона .

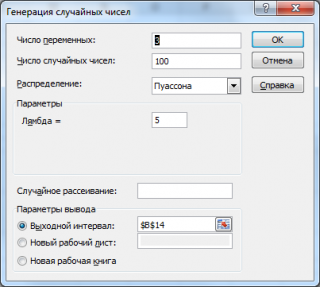
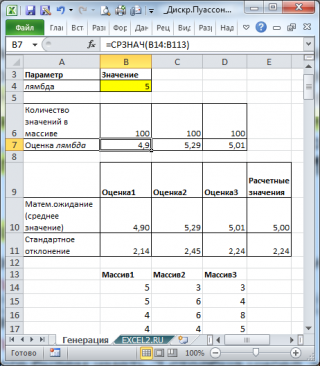
Сгенерируем 3 массива по 100 чисел с параметром λ=5. Для этого в окне Генерация случайных чисел установим следующие параметры:

В итоге будем иметь 3 столбца чисел, на основании которых можно оценить параметр λ для каждого массива с помощью функции СРЗНАЧ() , см. файл примера лист Генерация .

Связь Распределения Пуассона с Биномиальным и Нормальным распределением

Распределение Пуассона является предельным случаем Биномиального распределения , при условии, если параметр n Биномиального распределения стремится к бесконечности, а p – к 0.

Можно сформулировать условия, когда приближение распределением Пуассона работает хорошо:

• p <0,1 (чем меньше p и больше n, тем приближение точнее);
• p >0,9 (учитывая, что q =1- p , вычисления в этом случае необходимо производить через q (а х нужно заменить на n - x ). Следовательно, чем меньше q и больше n , тем приближение точнее).

Примечание : Если 0,1<=p<=0,9, а n*p>10, то Биномиальное распределение можно аппроксимировать Нормальным распределением .

При значениях λ >15 , Распределение Пуассона хорошо аппроксимируется Нормальным распределением со следующими параметрами: μ =λ , σ ² =λ .

Подробнее о связи этих распределений, можно прочитать в статье Взаимосвязь некоторых распределений в MS EXCEL . Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.

СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .