Распределение ХИ-квадрат. Распределения математической статистики в EXCEL
12 ноября 2016 г.
- Группы статей
- Распределения вероятностей
Рассмотрим Распределение ХИ-квадрат. С помощью функции MS EXCEL ХИ2.РАСП() построим графики функции распределения и плотности вероятности, поясним применение этого распределения для целей математической статистики.
Распределение ХИ-квадрат ( Х 2 , ХИ2, англ. Chi - squared distribution ) применяется в различных методах математической статистики:
- при построении доверительных интервалов для дисперсии ;
- при проверке гипотез о дисперсии нормального распределения ;
- при проверке гипотез с помощью критерия согласия Пирсона (согласуются ли эмпирические данные с нашим предположением о теоретической функции распределения или нет, англ. Goodness-of-fit)
- при проверке гипотез с помощью критерия независимости хи-квадрат (используется для определения связи между двумя категориальными переменными, англ. Chi-square test of association).
Определение : Если x 1 , x 2 , …, x n независимые случайные величины, распределенные по стандартному нормальному закону N(0;1), то распределение случайной величины Y=x 1 2 + x 2 2 +…+ x n 2 имеет распределение Х 2 с n степенями свободы.
Распределение Х 2 зависит от одного параметра, который называется степенью свободы ( df , degrees of freedom ). Например, при построении доверительных интервалов для оценки дисперсии число степеней свободы равно df=n-1, где n – размер выборки .
Плотность распределения
Х
2
выражается формулой:
![]()
при y>0
СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Графики функций
Распределение Х 2 имеет несимметричную форму, среднее значение равно n, дисперсия равна 2n.
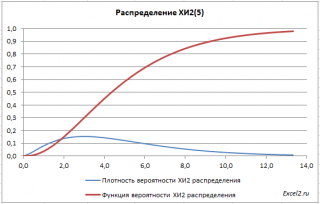
В файле примера на листе График приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Полезное свойство ХИ2-распределения
Пусть x 1 , x 2 , …, x n независимые случайные величины, распределенные по нормальному закону с одинаковыми параметрами μ и σ, а X cр является арифметическим средним этих величин x. Тогда случайная величина y равная
Имеет Х 2 -распределение с n-1 степенью свободы. Используя определение дисперсии выборки вышеуказанное выражение можно переписать следующим образом:
Следовательно, выборочное распределение статистики y, при выборке из нормального распределения , имеет Х 2 -распределение с n-1 степенью свободы.
Это свойство нам потребуется при построении доверительного интервала при оценке дисперсии распределения . Т.к. дисперсия может быть только положительным числом, а Х 2 -распределение используется для его оценки, то y д.б. >0, как и указано в определении.
ХИ2-распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Х 2 -распределения имеется специальная функция ХИ2.РАСП() , английское название – CHISQ.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина Х, имеющая ХИ2 - распределение , примет значение меньше или равное х, P{X <= x}).
Примечание : Т.к. ХИ2-распределение является частным случаем гамма распределения , то формула =ГАММА.РАСП(x;n/2;2;ИСТИНА) для целого положительного n возвращает тот же результат, что и формула =ХИ2.РАСП(x;n; ИСТИНА) или =1-ХИ2.РАСП.ПХ(x;n) . А формула =ГАММА.РАСП(x;n/2;2;ЛОЖЬ) возвращает тот же результат, что и формула =ХИ2.РАСП(x;n; ЛОЖЬ) , т.е. плотность вероятности ХИ2-распределения.
Функция ХИ2.РАСП.ПХ() возвращает функцию распределения , точнее - правостороннюю вероятность, т.е. P{X > x}. Очевидно, что справедливо равенство =ХИ2.РАСП.ПХ(x;n)+ ХИ2.РАСП(x;n;ИСТИНА)=1 т.к. первое слагаемое вычисляет вероятность P{X > x}, а второе P{X <= x}.
До MS EXCEL 2010 в EXCEL была только функция ХИ2РАСП() , которая позволяет вычислить правостороннюю вероятность, т.е. P{X > x}. Возможности новых функций MS EXCEL 2010 ХИ2.РАСП() и ХИ2.РАСП.ПХ() перекрывают возможности этой функции. Функция ХИ2РАСП() оставлена в MS EXCEL 2010 для совместимости.
ХИ2.РАСП() является единственной функцией, которая возвращает плотность вероятности ХИ2-распределения (третий аргумент должен быть равным ЛОЖЬ). Остальные функции возвращают интегральную функцию распределения , т.е. вероятность того, что случайная величина примет значение из указанного диапазона: P{X <= x}.
Вышеуказанные функции MS EXCEL приведены в файле примера на листе Функции .
Примеры
Найдем вероятность, что случайная величина Х примет значение меньше или равное заданного x : P{X <= x}. Это можно сделать несколькими функциями:
= ХИ2.РАСП(x; n; ИСТИНА) =1-ХИ2.РАСП.ПХ(x; n)=1-ХИ2РАСП(x; n)
Функция ХИ2.РАСП.ПХ() возвращает вероятность P{X > x}, так называемую правостороннюю вероятность, поэтому, чтобы найти P{X <= x}, необходимо вычесть ее результат от 1.
Найдем вероятность, что случайная величина Х примет значение больше заданного x : P{X > x}. Это можно сделать несколькими функциями:
= 1-ХИ2.РАСП(x; n; ИСТИНА) =ХИ2.РАСП.ПХ(x; n)=ХИ2РАСП(x; n)
Обратная функция ХИ2-распределения
Обратная функция используется для вычисления альфа - квантилей , т.е. для вычисления значений x при заданной вероятности альфа , причем х должен удовлетворять выражению P{X <= x}= альфа .
Функция ХИ2.ОБР() используется для вычисления доверительных интервалов дисперсии нормального распределения .
Функция ХИ2.ОБР.ПХ() используется для вычисления верхнего квантиля , т.е. если в качестве аргумента функции указан уровень значимости, например 0,05, то функция вернет такое значение случайной величины х, для которого P{X>x}=0,05. В качестве сравнения: функция ХИ2.ОБР() вернет такое значение случайной величины х, для которого P{X<=x}=0,05.
В MS EXCEL 2007 и ранее вместо ХИ2.ОБР.ПХ() использовалась функция ХИ2ОБР() .
Вышеуказанные функции можно взаимозаменять, т.к. следующие формулы возвращают один и тот же результат: =ХИ.ОБР(альфа;n) =ХИ2.ОБР.ПХ(1-альфа;n) =ХИ2ОБР(1- альфа;n)
Некоторые примеры расчетов приведены в файле примера на листе Функции .
Функции MS EXCEL, использующие ХИ2-распределение
В MS EXCEL имеется еще одна функция, использующая для расчетов ХИ2-распределение – это ХИ2.ТЕСТ() . Ее более ранняя версия - ХИ2ТЕСТ() . Подробнее об использовании этой функции см. статью про критерий независимости хи-квадрат .
Ниже приведено соответствие русских и английских названий функций: ХИ2.РАСП.ПХ() - англ. название CHISQ.DIST.RT, т.е. CHI-SQuared DISTribution Right Tail, the right-tailed Chi-square(d) distribution ХИ2.ОБР() - англ. название CHISQ.INV, т.е. CHI-SQuared distribution INVerse ХИ2.ПХ.ОБР() - англ. название CHISQ.INV.RT, т.е. CHI-SQuared distribution INVerse Right Tail ХИ2РАСП() - англ. название CHIDIST, функция эквивалентна CHISQ.DIST.RT ХИ2ОБР() - англ. название CHIINV, т.е. CHI-SQuared distribution INVerse
Оценка параметров распределения
Т.к. обычно ХИ2-распределение используется для целей математической статистики (вычисление доверительных интервалов, проверки гипотез и др.), и практически никогда для построения моделей реальных величин, то для этого распределения обсуждение оценки параметров распределения здесь не производится.
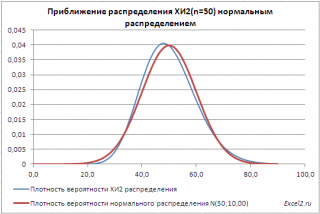
Приближение ХИ2-распределения нормальным распределением
При числе степеней свободы n>30
распределение Х
2
хорошо аппроксимируется
нормальным распределением
со
средним значением
μ=n и
дисперсией σ
=2*n (см.
файл примера лист Приближение
).
Комментарии