Поиск решения EXCEL (6.4). Кратчайший путь (неполный граф, линейная модель)

Необходимо найти кратчайший путь между 2-мя заданными городами. Построим линейную модель и с помощью надстройки Поиск решения решим задачу.

В статье Поиск решения MS EXCEL (6.3). Задача коммивояжера (полный граф, линейная модель) рассматривались модели, в которых  коммивояжёру требуется посетить все имеющиеся города. В этой задаче посещение всех городов не требуется.

Задача

Имеется 11 городов, координаты которых известны. Маршруты проложены только между некоторыми городами (неполный граф). Найти кратчайший путь между 2-мя заданными городами. Построить Линейную модель.

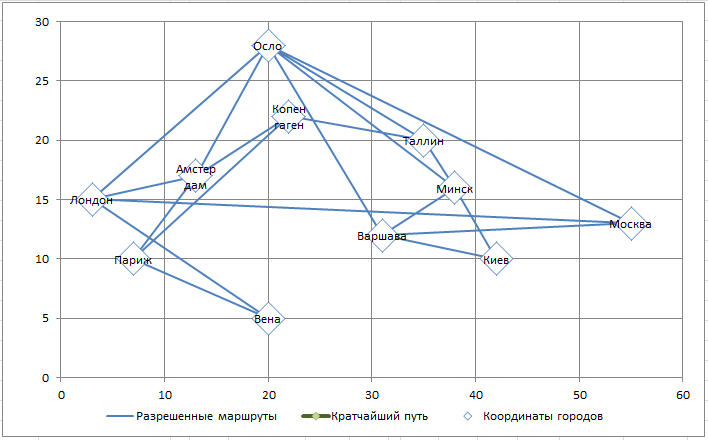
Создание модели

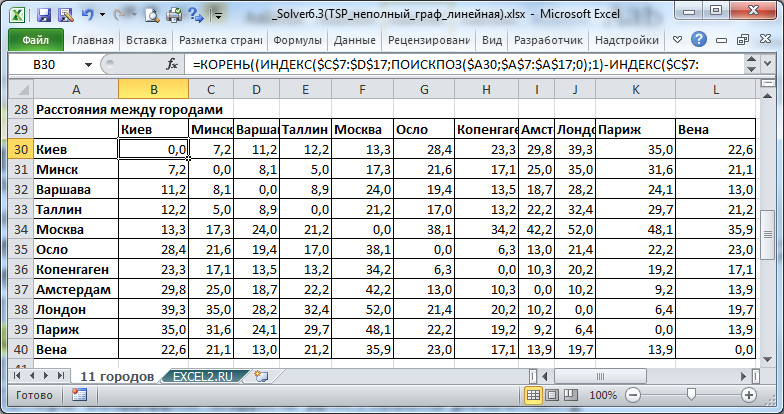
Так как даны координаты городов, то сначала найдем расстояния между ними (см. файл примера ).

Расстояния рассчитаем с помощью формулы: = КОРЕНЬ((ИНДЕКС($C$7:$D$17;ПОИСКПОЗ($A30;$A$7:$A$17;0);1)-ИНДЕКС($C$7:$D$17;ПОИСКПОЗ(B$29;$A$7:$A$17;0);1))^2 +(ИНДЕКС($C$7:$D$17;ПОИСКПОЗ($A30;$A$7:$A$17;0);2)-ИНДЕКС($C$7:$D$17;ПОИСКПОЗ(B$29;$A$7:$A$17;0);2))^2)

Теперь создадим линейную модель для решения задачи с помощью Поиска решения .

Совет : Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .

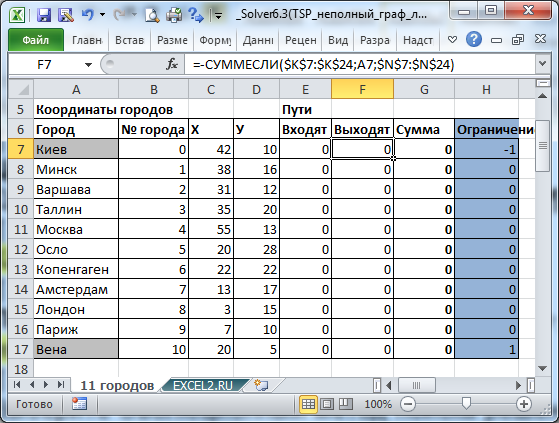
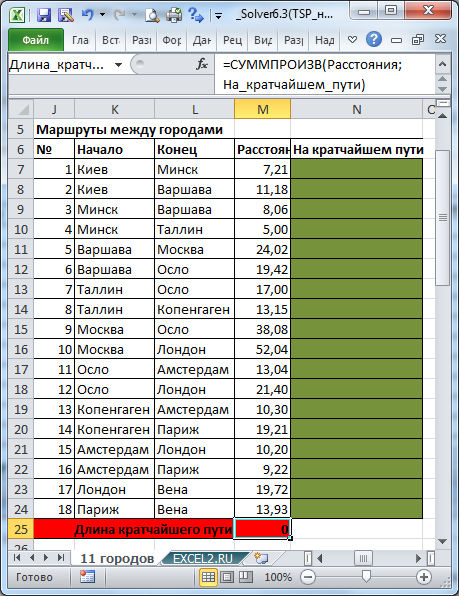
Обратите внимание, что не все города соединены сообщением (столбцы J:M), например нет прямого маршрута между Москвой и Парижем. Также для модели принципиально направление маршрута: Москва - Лондон, это не тоже самое, что Лондон-Москва (при необходимости список маршрутов можно расширить).

Переменные (выделено зеленым) . В качестве переменных модели следует взять номера маршрутов между городами: если маршрут включен в кратчайший путь, то переменная =1, если нет, то =0. Ограничения (выделено синим) . Необходимо, чтобы из каждого города, в котором побывал путешественник, был входящий и выходящий маршрут. Так как входящий маршрут обозначается 1, а исходящий -1, то их сумма, равная 0, будет означать, что в город вошли и вышли (включен в кратчайший путь). Исключение составляют город – начальная точка путешествия (сумма =-1) и город – конечная точка (сумма =1). Изменяя ограничение в синем столбце, можно задавать начальные и конечные пункты путешествия. Целевая функция (выделено красным) . Длина маршрута должна быть минимальной.

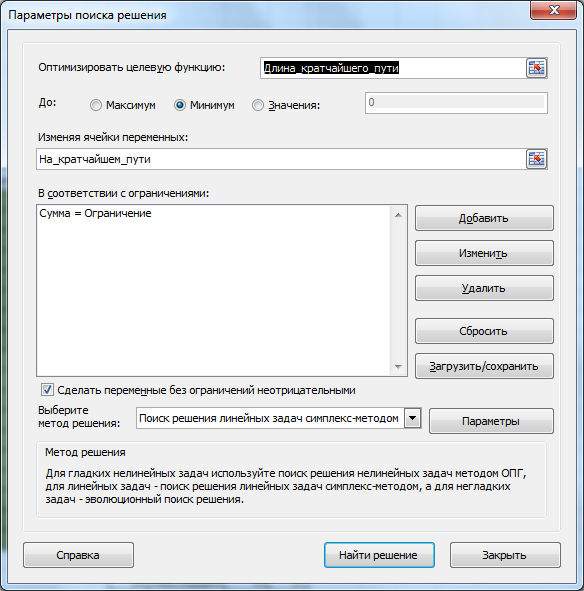
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .

Выберите Линейный метод поиска решения, т.к. созданная модель является линейной.

Найденное Решение

Поиск решения гарантировано найдет самый короткий маршрут, т.к. модель линейная.

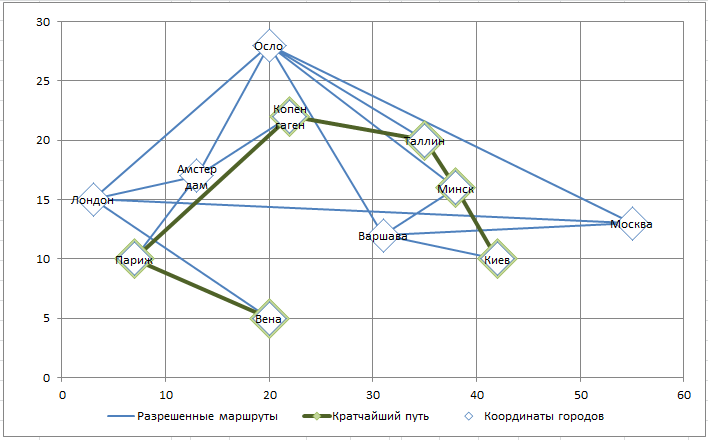
Изменив начальный и конечный пункт путешествия, и перезапустив Поиск решения , получим другой маршрут.

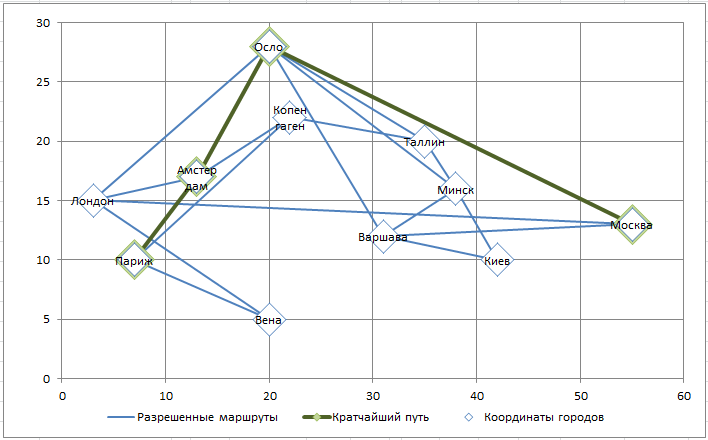
Будьте внимательны, не все пары конечных и начальных пунктов допустимы. Например, задав путешествие из Москвы в Копенгаген, Поиск решения не найдет маршрут, т.к. для этого потребуется «двигаться назад», а в маршрутах между городами обратные пути не прописаны (маршруты, конечно, можно добавить в столбцы J:M, но не забудьте изменить и другие формулы).