Поиск решения EXCEL (1.3). Распределение ресурсов (ограничение по количеству оборудования, несколько периодов)

Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). Расчет будем проводить с помощью надстройки Поиск решения.

Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты. Задача, в которой минимизируются затраты, понесенные в одном периоде решена в статье Поиск решения MS EXCEL (1.2). Распределение ресурсов (ограничение по количеству оборудования) , и имеет смысл предварительно познакомиться с изложенным там материалом. В этой статье мы решим аналогичную задачу, но для случая работы оборудования в нескольких периодах (пример с сайта ]]> www.solver.com ]]> ).

Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .

Задача

Предприятие выпускает монопродукт (только один вид изделия и ничего более) и ему необходимо выполнить заказ клиента. Выпуск продукции осуществляется в течение 5 дней. Отгрузка заказа ежедневная. На предприятии 3 типа оборудования. Каждый тип оборудования выпускает один и тот же продукт. Производительность каждого типа оборудования разная. Каждый тип оборудования имеет постоянную и переменную часть расходов. Переменная часть расходов пропорциональна количеству произведенных изделий. Имеется ограниченное количество единиц оборудования каждого типа (но общее количество оборудования избыточно для выполнения заказа). Требуется минимизировать расходы на оборудование при условии выполнения заказа.

Создание модели

На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).

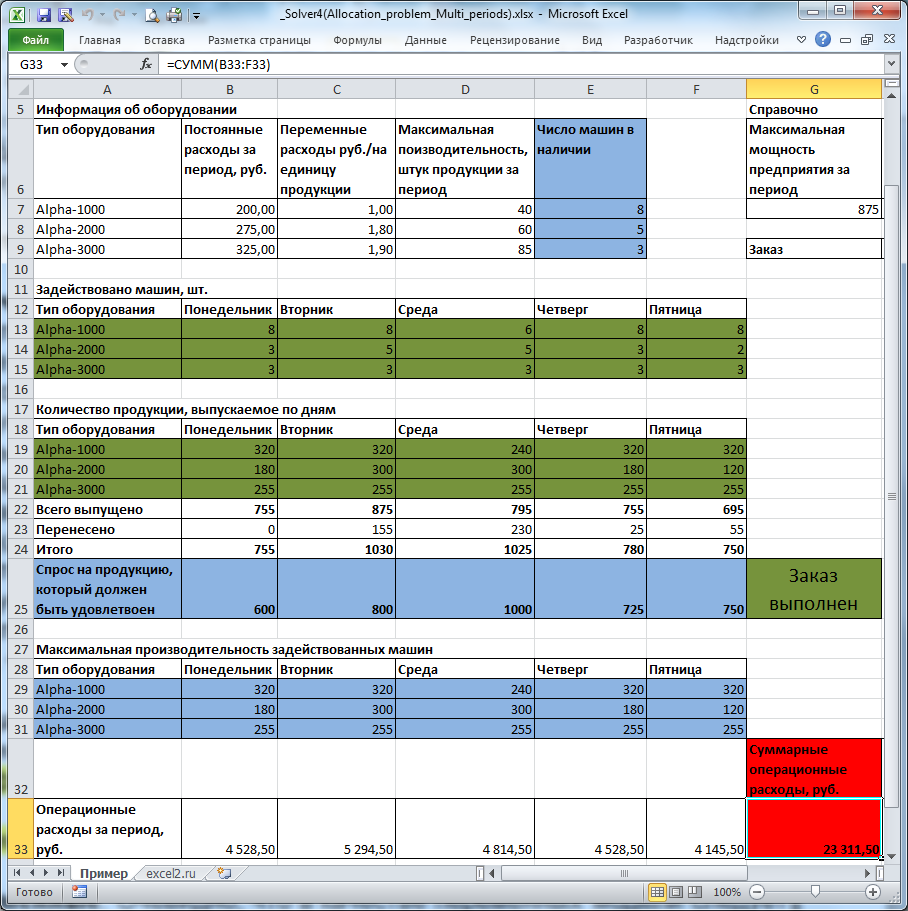
Предприятие несет расходы в зависимости от типа оборудования: использование оборудования типа Alpha-3000 самое дорогое в эксплуатации, но оно и самое производительное. Оборудование типа Alpha-1000 самое дешевое в эксплуатации, но оно и менее производительное. Задача Поиска решения выбрать наиболее дешевое оборудование, так чтобы заказ был выполнен (мощностей Alpha-1000 не хватит для выполнения заказа). Казалось бы, решение очевидно (взять по максимуму дешевое оборудование, остальную производительность обеспечить более дорогим). Однако, если учесть, что из-за низкой производительности дешевых машин приходится их брать больше, неся существенные постоянные расходы, то решение уже не кажется очевидным.

Переменные (выделено зеленым) . В качестве переменных модели следует взять количество задействованных единиц оборудования каждого типа и суммарное количество продукции, выпущенное на каждом типе оборудования (производительность задается не для каждой единицы, а для типа в целом). Для наглядности диапазонам ячеек, содержащих переменные, присвоены имена Машин_Задействовано и Продукции_выпущено.

Ограничения (выделено синим) . Количество задействованных машин должно быть целым числом. Количество задействованных машин каждого типа должно быть не больше, чем имеется в наличии (используются именованные диапазоны Alpha XXXX _Задействовано и Alpha XXXX _в_наличии ). Всего должно быть выпущено продукции не меньше чем величина заказа (используется именованный диапазон Продукции выпущено_Итого ). В день возможно производить больше продукции, чем требуется в день заказа, излишек переносится на следующий день. Также необходимо ограничить производительность задействованного оборудования. Производительность задается не для каждой единицы, а для типа в целом (используются именованные диапазоны Продукции выпущено и Макс_производительность_задейств_машин ).

Целевая функция (выделено красным) . Целевая функция – это сумма операционных расходов за 5 дней. Операционные расходы, понесенные за день, задается формулой =СУММПРОИЗВ(B19:B21; Расходы_переменные)+ СУММПРОИЗВ(B13:B15; Расходы_постоянные) B19:B21 – количество продукции, выпущенной в определенный день. B13:B15 - количество задействованных машин в определенный день.

Это суммарные операционные расходы (переменная и постоянные части). Сумма операционных расходов за 5 дней должна быть минимизирована.

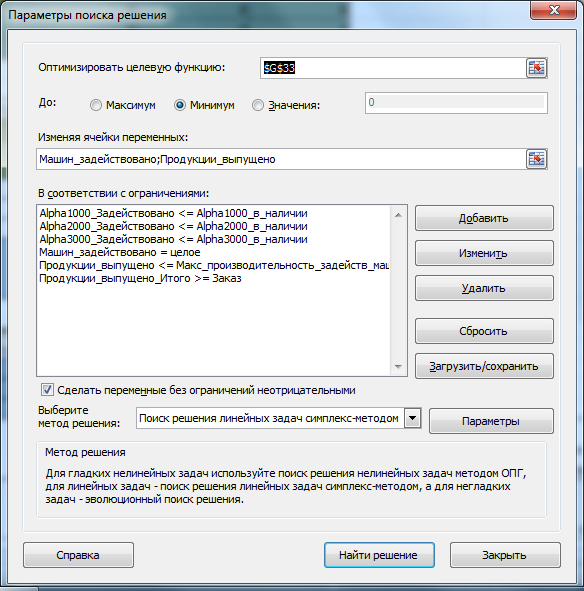
Убедитесь, что метод решения соответствует линейной задаче. Параметры Поиска решения были выбраны следующие:

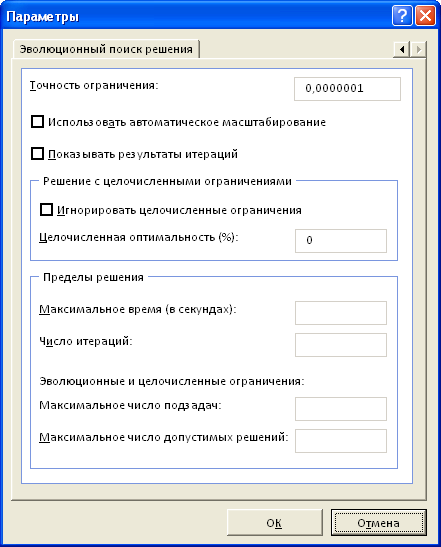
Теперь в диалоговом окне можно нажать кнопку Найти решение .

Результаты расчетов

Поиск решения подберет оптимальный набор единиц оборудования по типам и их производительность, при котором операционные расходы будут минимальные, а заказ выполнен. В нашей задаче было установлено целочисленное ограничение, что существенно усложняет задачу поиска и, соответственно, сказывается на скорости расчета. Как показано на рисунке выше, Целочисленная оптимальность была выбрана 0% ( Целочисленная оптимальность (Integer Optimality) позволяет Поиску решения остановить поиск, в случае, если он найдет целочисленное решение, в пределах указанного процента от оптимального). В нашем случае (0%), требуется найти лучшее из известных Поиску решения решений. Поиск в этом случае занял 8 секунд, результат 23 311,50. Установив Целочисленную оптимальность 1%, поиск займет 0,2 сек, результат 23 370,50 (отличие на 0,3%). Это информация к размышлению: стоит ли увеличение точности на 0,3% уменьшения скорости расчетов более чем на порядок? Решать Вам. В любом случае, первые расчеты модели лучше проводить при Целочисленной оптимальности не равной 0%.