Квартили и интерквартильный интервал (IQR) в EXCEL

Для вычисления квартилей в MS EXCEL существует специальная функция КВАРТИЛЬ() . В этой статье дадим определение квартилей и научимся их вычислять для выборки и для непрерывного распределения. Также вычислим интерквартильный интервал.

Квартили (Quartiles) — значения, которые делят выборку (набор значений) на четыре части, содержащие приблизительно равное количество наблюдений (по 25%).

Поясним определение квартиля на примере. Пусть имеется выборка , состоящая из 50 значений в ячейках А7:А56 (см. файл примера , лист Квартиль-выборка). Для наглядности отсортируем значения по возрастанию и построим гистограмму .

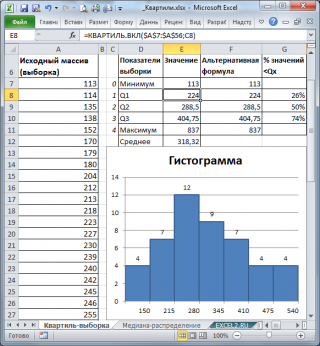
Чтобы разделить выборку на 4 части достаточно 3-х квартилей .

Первый квартиль (или нижний квартиль , Q1) делит выборку , на 2 части: примерно 25% значений в выборке меньше Q1, остальные 75% - больше. Для вычисления 1-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;1) . Для нашей выборки формула вернет значение 224. Значения 224 нет в выборке , формула произвела интерполяцию на основе 2-х соседних значений 223 и 227.

Примечание : Функция КВАРТИЛЬ.ВКЛ() появилась в MS EXCEL 2010. В более ранних версиях использовалась аналогичная ей функция КВАРТИЛЬ() .

Чтобы убедиться, что примерно 25% значений меньше, чем 224, используем формулу =СЧЁТЕСЛИ(A7:A56;"<"&224)/СЧЁТ(A7:A56) . В результате получим, что 26% меньше, чем 1-й квартиль .

Чем в выборке больше значений и меньше повторов , тем точнее деление выборки квартилями на четверти.

Примечание : Первый квартиль - это то же самое, что и 25-я процентиль . Подробнее см. статью про процентили .

Второй квартиль (или медиана , Q2) также делит выборку , на 2 равные части: половина чисел множества больше, чем медиана , а половина чисел меньше, чем медиана . Для вычисления 2-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;2) или =МЕДИАНА(A7:A56)

Третий квартиль (или верхний квартиль , Q3) делит выборку , на 2 части: примерно 75% значений в выборке меньше Q3, остальные 25% - больше. Для вычисления 3-го квартиля используйте формулу =КВАРТИЛЬ.ВКЛ(A7:A56;3) или =ПРОЦЕНТИЛЬ.ВКЛ(A7:A56;0,75)

Примечание : Третий квартиль - это то же самое, что и 75-я процентиль .

Второй аргумент функции КВАРТИЛЬ.ВКЛ() может также принимать значения 0 и 4. В первом случае функция вернет минимальное значение , во втором – максимальное .

Интерквартильный размах

Интерквартильным размахом или интерквартильным интервалом (InterQuartile range, IQR) называется разность между третьим и первым квартилями (Q3 - Q1). Интерквартильный размах является характеристикой разброса значений в выборке .

Примечание : Характеристикой разброса значений в выборке является также дисперсия и стандартное отклонение .

Интерквартильный размах , а также квартили используются при построении Блочной диаграммы , которая полезна для оценки разброса значений (variation) в небольших выборках или для сравнения нескольких выборок имеющих сходные распределения.

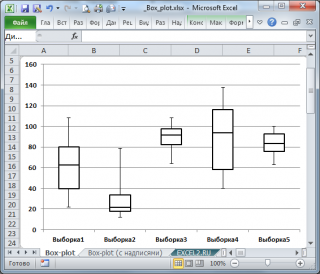
Подробнее о построении Блочной диаграммы см. статью Блочная диаграмма в MS EXCEL .

Квартили непрерывного распределения

Если функция распределения F (х) случайной величины х непрерывна, то 1-й квартиль является решением уравнения F(х) =0,25, второй - F(х) =0,5, а третий F(х) =0,75.

Примечание : Подробнее о Функции распределения см. статью Функция распределения и плотность вероятности в MS EXCEL .

Если известна функция плотности вероятности p (х) , то 1-й квартиль можно найти из уравнения:

Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ ² ), получим, что медиана (2-й квартиль ) вычисляется по формуле e ^μ или в MS EXCEL =EXP(μ). При μ=1, медиана равна 2,718.

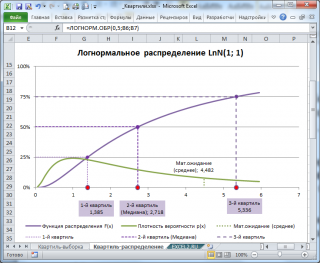
Обратите внимание на точку Функции распределения , для которой F(х)=0,5 (см. картинку выше или файл примера , лист Квартиль-распределение) . Абсцисса этой точки равна 2,718. Это и есть значение 2-го квартиля ( медианы ), что естественно совпадает с ранее вычисленным значением по формуле e ^μ .

Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице:

Поэтому, линии квартилей ( х=квартиль ) делят площадь под графиком функции плотности вероятности на 4 равные части.

Квартили в MS EXCEL

Чтобы вычислить в MS EXCEL квартили заданного распределения необходимо использовать соответствующую обратную функцию распределения .

При вычислении квартилей в MS EXCEL используются обратные функции распределения : НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР() , ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .

Например, в MS EXCEL 1-й квартиль для логнормального распределения LnN(1;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,25;1;1) , а 3-й квартиль для стандартного нормального распределения по формуле =НОРМ.СТ.ОБР(0,75) .