Квантили распределений EXCEL

Рассмотрим вычисление квантилей для некоторых функций распределений, представленных в MS EXCEL .

Понятие Квантиля основано на определении Функции распределения . Поэтому, перед изучением Квантилей рекомендуем освежить в памяти понятия из статьи Функция распределения вероятности .

Содержание статьи:

• Определение
• Квантили специальных видов
• Квантили стандартного нормального распределения
• Квантили распределения Стьюдента
• Квантили распределения ХИ-квадрат
• Квантили F-распределения
• Квантили распределения Вейбулла
• Квантили экспоненциального распределения

Сначала дадим формальное определение квантиля, затем приведем примеры их вычисления в MS EXCEL.

Определение

Пусть случайная величина X , имеет функцию распределения F ( x ). α-квантилем ( альфа- квантиль, x _a , квантиль порядка α, нижний α- квантиль ) называют решение уравнения x _a =F ^-1 (α), где α - вероятность, что случайная величина х примет значение меньшее или равное x _a , т.е. Р(х<= x _a )= α.

Из определения ясно, что нахождение квантиля распределения является обратной операцией нахождения вероятности. Т.е. если при вычислении функции распределения мы находим вероятность α, зная x _a , то при нахождении квантиля мы, наоборот, ищем x _a зная α .

Чтобы пояснить определение, используем график функции стандартного нормального распределения (см. файл примера Лист Определение ):

Примечание : О построении графиков в MS EXCEL можно прочитать статью Основные типы диаграмм в MS EXCEL .

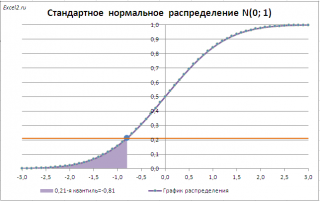
Например, с помощью графика вычислим 0,21-ю квантиль , т.е. такое значение случайной величины, что Р(X<=x _0,21 )=0,21.

Для этого найдем точку пересечения горизонтальной линии на уровне вероятности равной 0,21 с функцией распределения . Абсцисса этой точки равна -0,81. Соответственно, 0,21-я квантиль равна -0,81. Другими словами, вероятность того, что случайная величина, распределенная стандартному нормальному закону, примет значение меньше -0,81, равна 0,21 (21%).

Примечание : При вычислении квантилей в MS EXCEL используются обратные функции распределения : НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .

Точное значение квантиля в нашем случае можно найти с помощью формулы =НОРМ.СТ.ОБР(0,21)

СОВЕТ : Процедура вычисления квантилей имеет много общего с вычислением процентилей выборки (см. статью Процентили в MS EXCEL ).

Квантили специальных видов

Часто используются Квантили специальных видов:

• процентили x _p/100 , p=1, 2, 3, ..., 99
• квартили x _p/4 , p=1, 2, 3
• медиана x _1/2

В качестве примера вычислим медиану (0,5-квантиль) логнормального распределения LnN(0;1) (см. файл примера лист Медиана ).

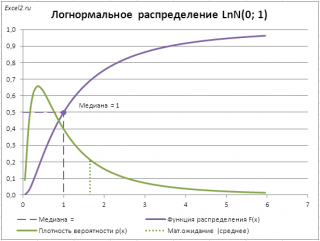
Это можно сделать с помощью формулы =ЛОГНОРМ.ОБР(0,5; 0; 1)

Квантили стандартного нормального распределения

Необходимость в вычислении квантилей стандартного нормального распределения возникает при проверке статистических гипотез и при построении доверительных интервалов.

Примечание : Про проверку статистических гипотез см. статью Проверка статистических гипотез в MS EXCEL . Про построение доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .

В данных задачах часто используется специальная терминология:

• Нижний квантиль уровня альфа ( α percentage point) ;
• Верхний квантиль уровня альфа (upper α percentage point) ;
• Двусторонние квантили уровня альфа .

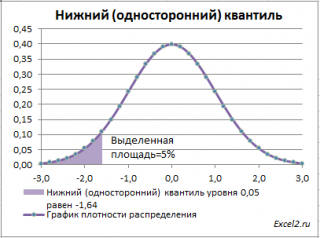
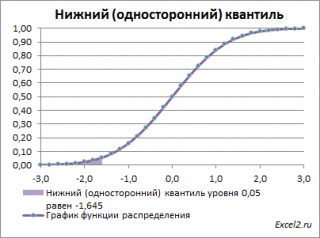
Нижний квантиль уровня альфа - это обычный α-квантиль. Чтобы пояснить название « нижний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения (см. файл примера лист Квантили ).

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение меньше α-квантиля . Из определения квантиля эта вероятность равна α . Из графика функции распределения становится понятно, откуда происходит название " нижний квантиль" - выделенная область расположена в нижней части графика.

Для α=0,05, нижний 0,05-квантиль стандартного нормального распределения равен -1,645. Вычисления в MS EXCEL можно сделать по формуле:

=НОРМ.СТ.ОБР(0,05)

Однако, при проверке гипотез и построении доверительных интервалов чаще используется "верхний" α-квантиль. Покажем почему.

Верхним α - квантилем называют такое значение x _α , для которого вероятность, того что случайная величина X примет значение больше или равное x _α равна альфа: P(X>= x _α )= α . Из определения понятно, что верхний альфа - квантиль любого распределения равен нижнему (1- α) - квантилю. А для распределений, у которых функция плотности распределения является четной функцией, верхний α - квантиль равен нижнему α - квантилю со знаком минус . Это следует из свойства четной функции f(-x)=f(x), в силу симметричности ее относительно оси ординат.

Действительно, для α=0,05, верхний 0,05-квантиль стандартного нормального распределения равен 1,645. Т.к. функция плотности вероятности стандартного нормального распределения является четной функцией, то вычисления в MS EXCEL верхнего квантиля можно сделать по двум формулам:

=НОРМ.СТ.ОБР(1-0,05)

=-НОРМ.СТ.ОБР(0,05)

Почему применяют понятие верхний α - квантиль? Только из соображения удобства, т.к. он при α<0,5 всегда положительный (в случае стандартного нормального распределения ). А при проверке гипотез α равно уровню значимости , который обычно берут равным 0,05, 0,1 или 0,01. В противном случае, в процедуре проверки гипотез пришлось бы записывать условие отклонения нулевой гипотезы μ>μ ₀ как Z ₀ >Z _{1- α} , подразумевая, что Z _{1- α} – обычный квантиль порядка 1- α (или как Z ₀ >-Z _α ). C верхнем квантилем эта запись выглядит проще Z ₀ >Z _α .

Примечание : Z ₀ - значение тестовой статистики , вычисленное на основе выборки . Подробнее см. статью Проверка статистических гипотез в MS EXCEL о равенстве среднего значения распределения (дисперсия известна) .

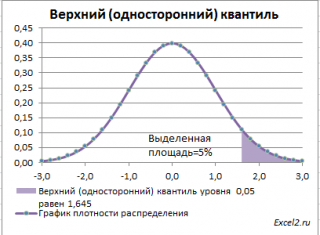
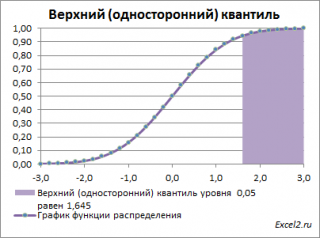
Чтобы пояснить название « верхний» квантиль , построим график плотности вероятности и функцию вероятности стандартного нормального распределения для α=0,05.

Выделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение больше верхнего 0,05-квантиля , т.е. больше значения 1,645. Эта вероятность равна 0,05.

На графике плотности вероятности площадь выделенной области равна 0,05 (5%) от общей площади под графиком (равна 1). Из графика функции распределения становится понятно, откуда происходит название "верхний" квантиль - выделенная область расположена в верхней части графика. Если Z ₀ больше верхнего квантиля , т.е. попадает в выделенную область, то нулевая гипотеза отклоняется.

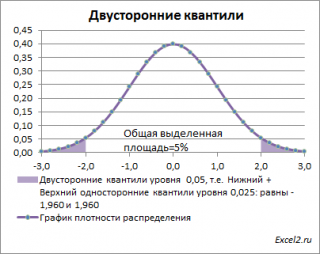
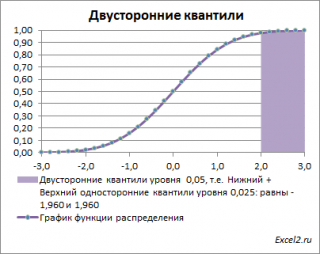
Также при проверке двухсторонних гипотез и построении соответствующих доверительных интервалов иногда используется понятие "двусторонний" α-квантиль. В этом случае условие отклонения нулевой гипотезы звучит как |Z ₀ |>Z _{α /2} , где Z _{α /2} – верхний α/2-квантиль . Чтобы не писать верхний α/2-квантиль , для удобства используют "двусторонний" α-квантиль. Почему двусторонний? Как и в предыдущих случаях, построим график плотности вероятности стандартного нормального распределения и график функции распределения .

Невыделенная площадь на рисунке соответствует вероятности, что случайная величина примет значение между нижним квантилем уровня α /2 и верхним квантилем уровня α /2, т.е. будет между значениями -1,960 и 1,960 при α=0,05. Эта вероятность равна в нашем случае 1-(0,05/2+0,05/2)=0,95. Если Z ₀ попадает в одну из выделенных областей, то нулевая гипотеза отклоняется.

Вычислить двусторонний 0,05 - квантиль это можно с помощью формул MS EXCEL: =НОРМ.СТ.ОБР(1-0,05/2) или =-НОРМ.СТ.ОБР(0,05/2)

Другими словами, двусторонние α-квантили задают интервал, в который рассматриваемая случайная величина попадает с заданной вероятностью α.

Квантили распределения Стьюдента

Аналогичным образом квантили вычисляются и для распределения Стьюдента . Например, вычислять верхний α/2- квантиль распределения Стьюдента с n -1 степенью свободы требуется, если проводится проверка двухсторонней гипотезы о среднем значении распределения при неизвестной дисперсии ( см. эту статью ).

Для верхних квантилей распределения Стьюдента часто используется запись t _α/2,n-1 . Если такая запись встретилась в статье про проверку гипотез или про построение доверительного интервала , то это именно верхний квантиль .

Примечание : Функция плотности вероятности распределения Стьюдента , как и стандартного нормального распределения , является четной функцией.

Чтобы вычислить в MS EXCEL верхний 0,05/2 - квантиль для t-распределения с 10 степенями свободы (или тоже самое двусторонний 0,05-квантиль ), необходимо записать формулу =СТЬЮДЕНТ.ОБР.2Х(0,05; 10) или =СТЬЮДРАСПОБР(0,05; 10) или =СТЬЮДЕНТ.ОБР(1-0,05/2; 10) или =-СТЬЮДЕНТ.ОБР(0,05/2; 10)

.2X означает 2 хвоста, т.е. двусторонний квантиль .

Квантили распределения ХИ-квадрат

Вычислять квантили распределения ХИ-квадрат с n -1 степенью свободы требуется, если проводится проверка гипотезы о дисперсии нормального распределения (см. статью Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения ).

При проверке таких гипотез также используются верхние квантили. Например, при двухсторонней гипотезе требуется вычислить 2 верхних квантиля распределения ХИ ² : χ ² _α/2,n-1 и χ ² _{1- α/2,n-1} . Почему требуется вычислить два квантиля , не один, как при проверке гипотез о среднем , где используется стандартное нормальное распределение или t-распределение ?

Дело в том, что в отличие от стандартного нормального распределения и распределения Стьюдента , плотность распределения ХИ ² не является четной (симметричной относительно оси х). У него все квантили больше 0, поэтому верхний альфа-квантиль не равен нижнему (1-альфа)-квантилю или по-другому: верхний альфа-квантиль не равен нижнему альфа-квантилю со знаком минус.

Чтобы вычислить верхний 0,05/2 - квантиль для ХИ ² -распределения с числом степеней свободы 10, т.е. χ ² _0,05/2,n-1 , необходимо в MS EXCEL записать формулу =ХИ2.ОБР.ПХ(0,05/2; 10) или =ХИ2.ОБР(1-0,05/2; 10)

Результат равен 20,48. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике функции распределения .

Чтобы вычислить верхний (1-0,05/2)- квантиль при том же числе степеней свободы , т.е. χ ² _1-0,05/2,n-1 и необходимо записать формулу =ХИ2.ОБР.ПХ(1-0,05/2; 10) или =ХИ2.ОБР(0,05/2; 10)

Результат равен 3,25.

Квантили F-распределения

Вычислять квантили распределения Фишера с n ₁ -1 и n ₂ -1 степенями свободы требуется, если проводится проверка гипотезы о равенстве дисперсий двух нормальных распределений (см. статью Двухвыборочный тест для дисперсии: F-тест в MS EXCEL ).

При проверке таких гипотез используются, как правило, верхние квантили. Например, при двухсторонней гипотезе требуется вычислить 2 верхних квантиля F -распределения: F _{α/2,n1-1, n 2 -1} и F _{1-α/2,n1-1, n 2 -1} . Почему требуется вычислить два квантиля , не один, как при проверке гипотез о среднем ? Причина та же, что и для распределения ХИ ² – плотность F-распределения не является четной . Эти квантили нельзя выразить один через другой как для стандартного нормального распределения . Верхний альфа-квантиль F -распределения не равен нижнему альфа-квантилю со знаком минус.

Чтобы вычислить верхний 0,05/2-квантиль для F -распределения с числом степеней свободы 10 и 12, необходимо записать формулу =F.ОБР.ПХ(0,05/2;10;12) =FРАСПОБР(0,05/2;10;12) =F.ОБР(1-0,05/2;10;12)

Результат равен 3,37. .ПХ означает правый хвост распределения, т.е. тот который расположен вверху на графике функции распределения .

Квантили распределения Вейбулла

Иногда обратная функция распределения может быть представлена в явном виде с помощью элементарных функций, например как для распределения Вейбулла . Напомним, что функция этого распределения задается следующей формулой:

После логарифмирования обеих частей выражения, выразим x через соответствующее ему значение F(x) равное P:

Примечание : Вместо обозначения α-квантиль может использоваться p - квантиль. Суть от этого не меняется.

Это и есть обратная функция, которая позволяет вычислить P - квантиль ( p - quantile ). Для его вычисления в формуле нужно подставить известное значение вероятности P и вычислить значение х _p (вероятность того, что случайная величина Х примет значение меньше или равное х _p равна P).

Квантили экспоненциального распределения

Задача : Случайная величина имеет экспоненциальное распределение :

Требуется выразить p -квантиль x _p через параметр распределения λ и заданную вероятность p .

Примечание : Вместо обозначения α-квантиль может использоваться p-квантиль . Суть от этого не меняется.

Решение : Вспоминаем, что p -квантиль – это такое значение x _p случайной величины X, для которого P(X<=x _p )= p . Т.е. вероятность, что случайная величина X примет значение меньше или равное x _p равна p . Запишем это утверждение с помощью формулы:

По сути, мы записали функцию вероятности экспоненциального распределения : F(x _p )= p .

Из определения квантиля следует, что для его нахождения нам потребуется обратная функция распределения .

Проинтегрировав вышеуказанное выражение, получим:

Используя это уравнение, выразим x _p через λ и вероятность p .

Конечно, явно выразить обратную функцию распределения можно не для всех функций распределений .