Двухвыборочный тест для дисперсии: F-тест в EXCEL

Рассмотрим использование MS EXCEL при проверке статистических гипотез о равенстве дисперсий 2-х нормальных распределений. Вычислим значение тестовой статистики F ₀ , рассмотрим процедуру «двухвыборочный F -тест», вычислим Р-значение (Р- value ), построим доверительный интервал. С помощью надстройки Пакет анализа сделаем «двухвыборочный F -тест для дисперсии».

Имеется две независимых случайных нормально распределенных величины . Эти случайные величины имеют нормальные распределения с неизвестными дисперсиями σ ₁ ² и σ ₂ ² соответственно. Из этих распределений получены две выборки размером n ₁ и n ₂ .

Необходимо произвести проверку гипотезы о равенстве дисперсий этих распределений (англ. Hypothesis Tests for the Equality of Variances of Two Normal Distributions).

СОВЕТ : Для проверки гипотез потребуется знание следующих понятий:

• дисперсия и стандартное отклонение ,
• выборочное распределение статистики ,
• уровень доверия/ уровень значимости ,
• распределение Фишера и его квантили .

Примечание : Провер ка гипотез о дисперсии нормального распределения ( одновыборочный тест ) изложена в статье Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения .

Нулевая гипотеза H ₀ звучит так: дисперсии нормальных распределений равны, т.е. σ ₁ ² = σ ₂ ² .

Альтернативная гипотеза H ₁ : σ ₁ ² <> σ ₂ ² . Т.е. нам требуется проверить двухстороннюю гипотезу .

В отличие от z-теста и t-теста , где мы рассматривали разность средних значений , в этом тесте будем рассматривать отношение дисперсий : σ ₁ ² / σ ₂ ² . Если дисперсии равны, то их отношение должно быть равно 1.

Как известно, точечной оценкой дисперсии распределения σ ² может служить значение дисперсии выборки s ² . Соответственно, оценкой отношения дисперсий σ ₂ ² / σ ₂ ² будет s ₁ ² / s ₂ ² .

Процедура проверки гипотезы о равенстве дисперсий 2-х распределений имеет специальное название: двухвыборочный F -тест для дисперсий (F-Test: Hypothesis Tests for the Variances of Two Normal Distributions).

Тестовой статистикой для проверки гипотез данного вида является случайная величина F= s ₁ ² / s ₂ ² .

Данная тестовая статистика , как и любая другая случайная величина, имеет свое распределение (в процедуре проверки гипотез это распределение называют « эталонным распределением », англ. Reference distribution). В нашем случае F -статистика имеет F-распределение (распределение Фишера) . Значение, которое приняла F -статистика обозначим F ₀ .

Примечание : В статье Статистики и их распределения показано , что выборочное распределение статистики при достаточно большом размере выборок стремится к F-распределению вероятности с n ₁ -1 и n ₂ -1 степенями свободы .

Установим требуемый уровень значимости α (альфа) (допустимую для данной задачи ошибку первого рода , т.е. вероятность отклонить нулевую гипотезу , когда она верна).

Мы будем отклонять нулевую двухстороннюю гипотезу, если F ₀ , вычисленное на основании выборок , примет значение:

• больше верхнего α/2-квантиля F-распределения вероятности с n ₁ -1 и n ₂ -1 степенями свободы или
• меньше нижнего α/2-квантиля того же распределения.

Примечание : Верхний α/2-квантиль - это такое значение случайной величины F , что P ( F >= F _{α /2, n1-1, n2-1} )=α/2. Верхний 1-α /2- квантиль равен нижнему α/2 квантилю . Подробнее о квантилях распределений см. статью Квантили распределений MS EXCEL .

Запишем критерий отклонения с помощью верхних квантилей:

• F ₀ > F _{α /2, n1-1, n2-1} или
• F ₀ < F _{1-α /2, n1-1, n2-1}

Чтобы в MS EXCEL вычислить значение верхнего α/2-квантиля для различных уровней значимости (10%; 5%; 1%) и степеней свободы, т.е. F _{α /2, n1-1, n2-1} - используйте формулу =F.ОБР.ПХ(α /2 ; n ₁ -1, n ₂ -1) или =F.ОБР(1-α /2 ; n ₁ -1, n ₂ -1)

Чтобы в MS EXCEL вычислить значение нижнего квантиля α/2-квантиля - используйте формулу =F.ОБР(α /2 ; n ₁ -1, n ₂ -1) или =F.ОБР.ПХ(1-α /2 ; n ₁ -1, n ₂ -1)

Проверка двухсторонней гипотезы приведена в файле примера .

F-тест обычно используется для того, чтобы ответить на следующие вопросы:

• Взяты ли 2 выборки из генеральных совокупностей с равными дисперсиями ?
• Привели ли изменения, внесенные в технологический процесс (новая термообработка, замена химического компонента и пр.), к снижению вариабельности текущего процесса?

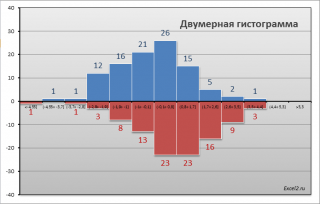
СОВЕТ : Перед проверкой гипотез о равенстве дисперсий полезно построить двумерную гистограмму , чтобы визуально определить разброс данных в обеих выборок .

Доверительный интервал

В файле примера для двустороннего F-теста вычислены границы соответствующего двустороннего доверительного интервала .

В файле примера также показана эквивалентность проверки гипотезы через доверительный интервал , статистику F ₀ ( F -тест) и p -значение (см. ниже) .

Вычисление Р-значения

При проверке гипотез, помимо F -теста, большое распространение получил еще один эквивалентный подход, основанный на вычислении p -значения (p-value).

Если p-значение меньше, чем заданный уровень значимости α , то нулевая гипотеза отвергается и принимается альтернативная гипотеза . И наоборот, если p-значение больше α, то нулевая гипотеза не отвергается.

В случае двусторонней гипотезы p-значение вычисляется следующим образом:

• если F ₀ >1, то p-значение равно удвоенной вероятности, что F -статистика примет значение больше F ₀ ,
• если F ₀ <1, то p-значение равно удвоенной вероятности, что F -статистика примет значение меньше F ₀ .

В MS EXCEL соответствующая формула для вычисления p -значения в случае двухсторонней гипотезы : =2*МИН(F.РАСП(F ₀ ; n ₁ -1; n ₂ -1; ИСТИНА); F.РАСП.ПХ(F ₀ ; n ₁ -1; n ₂ -1))

Почему вычисляется удвоенная вероятность? Представим, что установлен уровень доверия 0,05, а F ₀ <1. Если F ₀ больше нижнего 0,025-квантиля , то вероятность, что F -статистика примет значение меньше этого квантиля будет больше 0,025. Поэтому, у нас нет основания отклонить нулевую гипотезу (см. раздел про F -тест ). Однако, мы помним, p-значение сравнивается с уровнем значимости 0,05, а не 0,05/2=0,025. Поэтому, нужно удвоить значение вероятности.

Примечание : Про p -значение можно также прочитать в статье про двухвыборочный z-тест .

Функция F.ТЕСТ()

Функция F.ТЕСТ() возвращает p-значение в случае двусторонней гипотезы.

Функция имеет только 2 аргумента: массив1 и массив2 , в которых указываются ссылки на диапазоны ячеек, содержащих выборки .

Таким образом, функция F.ТЕСТ() эквивалентна вышеуказанной формуле =2*МИН(F.РАСП(F ₀ ; n ₁ -1; n ₂ -1; ИСТИНА); F.РАСП.ПХ(F ₀ ; n ₁ -1; n ₂ -1))

где F ₀ – это отношение дисперсий выборок, n ₁ и n ₂ – размеры выборок .

Функцию F.ТЕСТ() можно использовать и при проверке односторонних гипотез – для этого нужно разделить ее результат на 2.

Пакет анализа

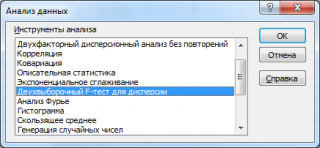
В надстройке Пакет анализа для проведения двухвыборочного F -теста имеется специальный инструмент: Двухвыборочный F-тест для дисперсии (F-Test Two Sample for Variances).

После выбора инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Пакет анализа ):

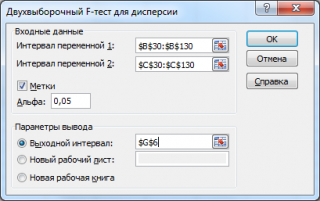
• интервал переменной 1 : ссылка на значения первой выборки . Ссылку указывать лучше с заголовком. В этом случае, при выводе результата надстройка выводит заголовки, которые делают результат нагляднее (в окне требуется установить галочку Метки );
• интервал переменной 2 : ссылка на значения второй выборки ;
• Метки: если в полях интервал переменной 1 и интервал переменной 2 указаны ссылки вместе с заголовками столбцов, то эту галочку нужно установить. В противном случае надстройка не позволит провести вычисления и пожалуется, что « входной интервал содержит нечисловые данные »;
• Альфа: уровень значимости ;
• Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.

В результате вычислений будет заполнен указанный Выходной интервал.

Тот же результат можно получить с помощью формул (см. файл примера лист Пакет анализа ):

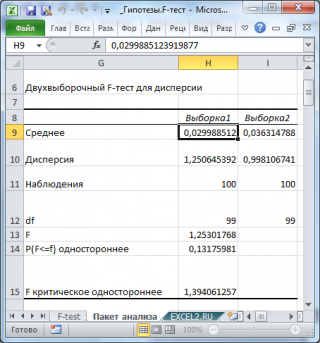
Разберем результаты вычислений, выполненных надстройкой:

• Среднее : средние значения обеих выборок . Вычисления можно сделать с помощью функции СРЗНАЧ() . Значения средних в расчетах для проверки гипотез не участвуют и приводятся для информации;
• Дисперсия : дисперсии обеих выборок. Вычисления можно сделать с помощью функции ДИСП.В()
• Наблюдения : размер выборок. Вычисления можно сделать с помощью функции СЧЁТ()
• Df : число степеней свободы : n-1, где n размер выборок ;
• F : значение тестовой F -статистики (в наших обозначениях – это F ₀ – отношение дисперсий выборок );
• P( F <= f ) одностороннее : р-значение в случае односторонней альтернативной гипотезы σ ₁ ² > σ ₂ ² . Эквивалентная формула =F.РАСП.ПХ(F ₀ ;n ₁ -1; n ₂ -1) ;
• F критическое одностороннее (F Critical one-tail): Верхний α-квантиль F -распределения c n ₁ -1 и n ₂ -1 степенями свободы . Эквивалентная формула =F.ОБР.ПХ(α; n ₁ -1; n ₂ -1) .

СОВЕТ : О проверке других видов гипотез см. статью Проверка статистических гипотез в MS EXCEL .