Двухвыборочный t-тест с одинаковыми дисперсиями в EXCEL
11 декабря 2016 г.
- Группы статей
- Статистический вывод
Рассмотрим использование MS EXCEL при проверке статистических гипотез о разнице средних значений 2-х распределений в случае неизвестных дисперсий (дисперсии этих 2-х распределений одинаковы). Вычислим значение тестовой статистики t 0 , рассмотрим соответствующую процедуру «двухвыборочный t -тест», вычислим Р-значение (Р- value ). С помощью надстройки Пакет анализа сделаем «Двухвыборочный t-тест с одинаковыми дисперсиями».
Имеется две независимых случайных величины. Эти случайные величины имеют распределения с неизвестными средними значениями μ 1 и μ 2 . Дисперсии этих распределений неизвестны, но равны между собой ( дисперсию обозначим σ 2 ). Из этих распределений получены две выборки размером n 1 и n 2 .
Необходимо произвести проверку гипотезы о разнице средних значений этих распределений: μ 1 - μ 2 (англ. Hypothesis tests for a difference in means, populations with unknown but equal variances).
Нулевая гипотеза H 0 звучит так: разница средних значений равна Δ 0 , т.е. Δ 0 = (μ 1 - μ 2 ). Часто предполагается, что Δ 0 =0, следовательно, μ 1 = μ 2 (значение Δ 0 задается исследователем исходя из условий решаемой задачи).
Альтернативная гипотеза H 1 : (μ 1 - μ 2 )<>Δ 0 . Т.е. нам требуется проверить двухстороннюю гипотезу .
Примечание : Про построение соответствующего двухстороннего доверительного интервала можно прочитать в этой статье Доверительный интервал для разницы средних значений 2-х распределений (дисперсии неизвестны, но равны) в MS EXCEL .
СОВЕТ : При первом знакомстве с процедурой двухвыборочного t -теста может быть полезным освежить в памяти процедуру одновыброчного t-теста для среднего при неизвестной дисперсии .
СОВЕТ : Для проверки гипотез нам потребуется знание следующих понятий:
- дисперсия и стандартное отклонение ,
- выборочное распределение статистики ,
- уровень доверия/ уровень значимости ,
- нормальное распределение ,
- t-распределение Стьюдента и его квантили .
Примечание : Вышеуказанные распределения не обязательно должны быть нормальными . Однако, требуется чтобы выполнялись условия применимости Центральной предельной теоремы . Если размеры выборок меньше 30, то для справедливости сделанных здесь выводов, необходимо, чтобы выборки были сделаны из нормального распределения .
Сначала дадим точечную оценку для Δ 0 .
Точечной оценкой для Δ 0 или для μ 1 - μ 2 является разница между средними значениями, вычисленными на основании выборок из этих (независимых) распределений, т.е. Хср 1 - Хср 2 . Это следует из свойства математического ожидания : Е(Хср 1 - Хср 2 )= Е(Хср 1 )-Е(Хср 2 )= μ 1 - μ 2
Хср 1 - Хср 2 является случайной величиной, и как любая другая случайная величина, она имеет свое распределение вероятности. В данном случае, эта случайная величина распределена по нормальному закону . Это следует из того, что Хср 1 и Хср 2 распределены по нормальному закону (см. статью про ЦПТ ), а их линейная комбинация Хср 1 - Хср 2 также имеет нормальное распределение (см. статью про нормальное распределение ).
Теперь вычислим дисперсию этого распределения. На основании свойств дисперсии имеем, что VAR(Хср 1 - Хср 2 )= VAR(Хср 1 )+ VAR(Хср 2 ) = σ 2 /n 1 + σ 2 /n 2 =σ 2 (1/n 1 + 1/n 2 ).
Т.к. дисперсия σ 2 нам неизвестна, то вместо нее используем ее оценку: так называемую объединенную оценку дисперсии s p 2 (pooled estimate of variance).
Воспользуемся результатами статьи про двухвыборочный z-тест .
Из процедуры двухвыборочного z-теста известно, что тестовая статистика Z имеет стандартное нормальное распределение .
где Хср 1 и Хср 2 – средние выборок , а n 1 и n 2 – размеры этих выборок .
Заменив, неизвестное значение
стандартного отклонения
σ на ее оценку s
p
, получим величину t:
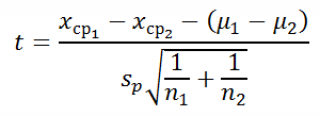
Эта величина является тестовой статистикой ( t -статистикой ) для нашего двухвыборочного t -теста с одинаковыми дисперсиями . Известно, что t -статистика имеет распределение Стьюдента с n 1 +n 2 –2 степенями свободы. Значение, которое приняла t -статистика обозначим t 0 .
Как и для z -теста , проверка двухсторонней гипотезы сводится к сравнению t 0 с квантилями эталонного распределения , в данном случае распределения Стьюдента с n 1 +n 2 –2 степенями свободы. Эта процедура носит название двухвыборочный t -тест в случае одинаковых дисперсий (The two-sample pooled t-Test).
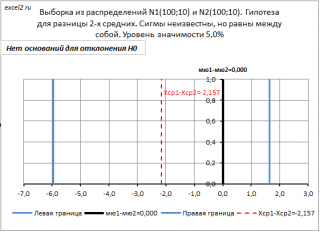
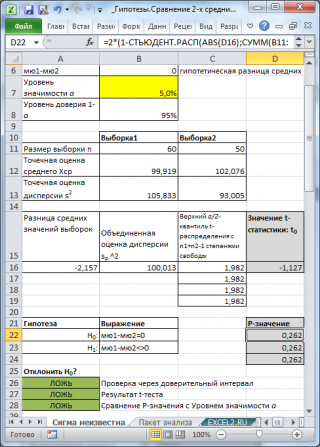
Если вычисленное на основе выборок значение t 0 , в случае двухсторонней гипотезы , не попадет в область значений ограниченной нижним и верхним α /2-квантилями t - распределения с n 1 +n 2 –2 степенями свободы , то у нас будет основание отвергнуть нулевую гипотезу. Это утверждение эквивалентно случаю, когда Хср 1 -Хср 2 окажется вне пределов соответствующего доверительного интервала . В файле примера на листе Сигма неизвестна показана эквивалентность доверительного интервала и соответствующего двухвыборочного t -теста.
Примечание : Про построение соответствующего двухстороннего доверительного интервала можно прочитать в этой статье Доверительный интервал для разницы средних значений 2-х распределений (дисперсии неизвестны, но равны) в MS EXCEL .
Примечание : Верхний α /2-квантиль - это такое значение случайной величины t n1+n2–2 , что P ( t n1+n2–2 >= t α /2, n1+n2–2 )= α /2. Подробнее о квантилях распределений см. статью Квантили распределений MS EXCEL .
В нашем случае, необходимо будет вычислить только верхний α /2-квантиль, т.к. он равен соответствующему нижнему квантилю со знаком минус. Следовательно, условие отклонения нулевой гипотезы можно записать как | t 0 |>t α/2 , n1+n2–2 .
Чтобы в MS EXCEL вычислить значение t α/2 , n1+n2–2 для различных уровней значимости (10%; 5%; 1%) и степеней свобод можно использовать несколько формул: =СТЬЮДЕНТ.ОБР.2Х( α ; n 1 +n 2 –2) =СТЬЮДЕНТ.ОБР(1- α /2; n 1 +n 2 –2) =-СТЬЮДЕНТ.ОБР( α /2; n 1 +n 2 –2) =СТЬЮДРАСПОБР( α ; n 1 +n 2 –2)
Примечание : Подробнее про функции MS EXCEL, связанные с t - распределением см. статью t-распределение .
Итак, если при проверке двухсторонней гипотезы формула =ABS( t 0 ) вернет значение больше, чем результат формулы =СТЬЮДЕНТ.ОБР.2Х( α ; n 1 +n 2 –2) , то это означает, что необходимо отвергнуть нулевую гипотезу (вычисления приведены в файле примера на листе Сигма неизвестна ) .
Для односторонней альтернативной гипотезы (μ 1 - μ 2 )>Δ 0 , нулевая гипотеза будет отвергнута в случае t 0 >t α , n1+n2–2 .
Для односторонней альтернативной гипотезы (μ 1 - μ 2 )<Δ 0 , нулевая гипотеза будет отвергнута в случае t 0 <-t α , n1+n2–2 .
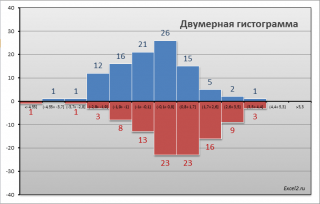
СОВЕТ : Перед проверкой гипотез о равенстве средних значений полезно построить двумерную гистограмму , чтобы визуально определить центральную тенденцию и разброс данных в обеих выборок .
Вычисление Р-значения
При проверке гипотез, помимо t -теста, большое распространение получил еще один эквивалентный подход, основанный на вычислении p -значения (p-value).
Если p-значение меньше чем заданный уровень значимости α , то нулевая гипотеза отвергается и принимается альтернативная гипотеза . И наоборот, если p-значение больше α , то нулевая гипотеза не отвергается.
В случае двусторонней гипотезы p-значение равно суммарной вероятности, что t -статистика примет значение больше | t 0 | и меньше -| t 0 |.
Подробнее про p -значение см., например, статью про двухвыборочный z-тест .
В MS EXCEL p -значение для двухсторонней гипотезы вычисляется по формуле: =2*(1-СТЬЮДЕНТ.РАСП(ABS( t 0 ); n 1 +n 2 –2;ИСТИНА))
Примечание : Вычисления приведены в файле примера на листе Сигма неизвестна .
Для односторонней гипотезы μ 1 - μ 2 > Δ 0 p -значение вычисляется по формуле: =1-СТЬЮДЕНТ.РАСП( t 0 ; n 1 +n 2 –2;ИСТИНА) В этом случае p-значение равно вероятности, что t -статистика примет значение больше t 0 .
Для односторонней гипотезы μ 1 - μ 2 < Δ 0 p -значение вычисляется по формуле: =СТЬЮДЕНТ.РАСП( t 0 ; n 1 +n 2 –2;ИСТИНА) В этом случае p-значение равно вероятности, что t -статистика примет значение меньше t 0 .
В файле примера на листе Сигма неизвестна показана эквивалентность проверки гипотезы через доверительный интервал , статистику t 0 ( t -тест) и p -значение .
В MS EXCEL есть функция СТЬЮДЕНТ.TEСT() , которая вычисляет p-значение для 3-х различных двухвыборочных t -тестов (см. следующий раздел статьи) . К сожалению, эта функция может быть использована только для проверки гипотез с Δ 0 =0, то есть для проверки гипотез о равенстве средних μ 1 = μ 2 . Об этом легко догадаться, т.к. среди ее параметров отсутствует параметр Гипотетическая разность средних , т.е. Δ 0 .
Функция СТЬЮДЕНТ.ТЕСТ()
Функция СТЬЮДЕНТ.ТЕСТ() используется для оценки различия двух выборочных средних . До MS EXCEL 2010 имелась аналогичная функция ТТЕСТ() .
Примечание : В английской версии функция носит название T.TEST() , старая версия - TTEST() .
Функция СТЬЮДЕНТ.ТЕСТ() имеет 4 параметра. Первые два – это ссылки на диапазоны ячеек, содержащие выборки из 2-х сравниваемых распределений.
Третий параметр имеет название «хвосты». Этот параметр задает тип проверяемой гипотезы: односторонняя (=1) или двухсторонняя (=2). Если мы проверяем двухстороннюю гипотезу , то смотрим, не попало ли значение тестовой статистики t 0 в один из 2-х хвостов соответствующего t-распределения . Если мы проверяем одностороннюю гипотезу (имеется ввиду гипотеза μ 1 < μ 2 ), то «хвост» всего один.
Как было сказано выше, эта функция вычисляет p -значение для 3-х различных двухвыборочных t -тестов . За это отвечает четвертый параметр функции, который принимает значения от 1 до 3:
- Парный двухвыборочный t-тест для средних ;
- Двухвыборочный t-тест с одинаковыми дисперсиями ;
- Двухвыборочный t-тест с разными дисперсиями .
Таким образом, p -значение для двухсторонней гипотезы (равные дисперсии ) вычисляется по формуле (см. файл примера ): =СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 2; 2) или =2*(1-СТЬЮДЕНТ.РАСП(ABS( t 0 ); n 1 +n 2 –2;ИСТИНА))
Для односторонней гипотезы μ 1 < μ 2 p -значение вычисляется по формуле: =СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 1; 2) или =СТЬЮДЕНТ.РАСП( t 0 ; n 1 +n 2 –2;ИСТИНА)
Для односторонней гипотезы μ 1 > μ 2 p -значение вычисляется по формуле: =1-СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 1; 2) или =1-СТЬЮДЕНТ.РАСП( t 0 ; n 1 +n 2 –2;ИСТИНА)
Пакет анализа
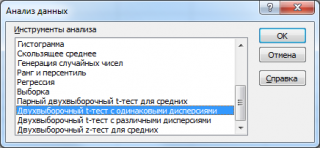
В надстройке Пакет анализа для проведения двухвыборочного t -теста с одинаковыми дисперсиями имеется специальный инструмент: Двухвыборочный t -тест с одинаковыми дисперсиями (t-Test: Two-Sample Assuming Equal Variances).
После выбора инструмента откроется окно, в котором требуется заполнить следующие поля (см. файл примера лист Пакет анализа ):
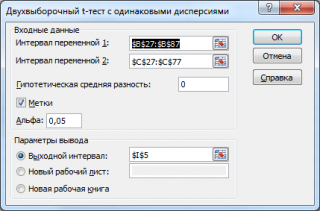
- интервал переменной 1 : ссылка на значения первой выборки . Ссылку указывать лучше с заголовком. В этом случае, при выводе результата надстройка выводит заголовки, которые делают результат нагляднее (в окне требуется установить галочку Метки );
- интервал переменной 2 : ссылка на значения второй выборки ;
- гипотетическая средняя разность : укажите значение Δ 0 , т.е. μ 1 - μ 2 . В нашем случае, введем 0;
- Метки: если в полях интервал переменной 1 и интервал переменной 2 указаны ссылки вместе с заголовками столбцов, то эту галочку нужно установить. В противном случае надстройка не позволит провести вычисления и пожалуется, что « входной интервал содержит нечисловые данные »;
- Альфа: уровень значимости α;
- Выходной интервал: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
В результате вычислений будет заполнен указанный Выходной интервал.
Тот же результат можно получить с помощью формул (см. файл примера лист Пакет анализа ):
Разберем результаты вычислений, выполненных надстройкой:
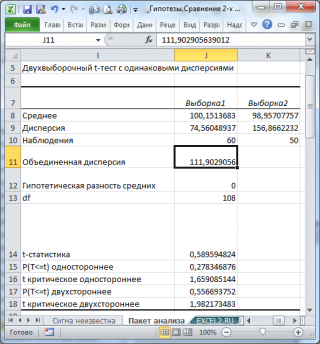
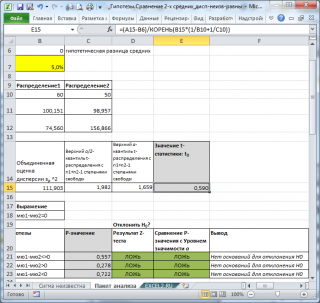
- Среднее : средние значения обеих выборок Хср 1 и Хср 2 . Вычисления можно сделать с помощью функции СРЗНАЧ() ;
- Дисперсия : дисперсии обеих выборок. Вычисления можно сделать с помощью функции ДИСП.В()
- Наблюдения : размер выборок. Вычисления можно сделать с помощью функции СЧЁТ() ;
- Объединенная дисперсия : Объединенная оценка дисперсии, т.е.величина s p 2 ;
- Df : число степеней свободы, т.е. величина n 1 +n 2 –2;
- t -статистика : значение тестовой статистики t (в наших обозначениях – это t 0 ). Вычисление t 0 приведено в ячейке Е15 ;
- P(T<=t) одностороннее : р-значение в случае односторонней альтернативной гипотезы μ 1 - μ 2 >Δ 0 . Эквивалентная формула =1-СТЬЮДЕНТ.РАСП( t 0 ; n 1 +n 2 –2;ИСТИНА) ;
- t критическое одностороннее : Верхний α-квантиль t-распределения . Эквивалентная формула =СТЬЮДЕНТ.ОБР(1- α; n 1 +n 2 –2) ;
- P(T<=t) двухстороннее: р-значение в случае двухсторонней альтернативной гипотезы μ 1 - μ 2 <>Δ 0 . Эквивалентная формула =2*(1-СТЬЮДЕНТ.РАСП(ABS( t 0 ); n 1 +n 2 –2;ИСТИНА)) ;
- t критическое двухстороннее: Верхний α/2-Квантиль t-распределения . Эквивалентная формула =СТЬЮДЕНТ.ОБР(1- α/2; n 1 +n 2 –2) .
СОВЕТ : О проверке других видов гипотез см. статью Проверка статистических гипотез в MS EXCEL .
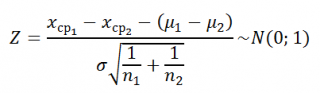
Комментарии