Доверительный интервал для разницы средних значений 2-х распределений (дисперсии известны) в EXCEL

Построим доверительный интервал для разницы средних значений 2-х распределений в случае известных дисперсий.

Имеется две независимых случайных величины. Эти случайные величины имеют распределения с неизвестными средними значениями μ ₁ и μ ₂ . Дисперсии этих распределений известны и равны σ ₁ ² и σ ₂ ² соответственно (в общем случае дисперсии могут быть не равны). Из этих распределений получены две выборки размером n ₁ и n ₂ (в общем случае размеры выборок также могут быть не равны между собой).

Формулировка задачи. Нас интересует разница средних значений этих распределений: μ ₁ - μ ₂ . Мы делаем предположение, что эта разница равна Δ ₀ , т.е. Δ ₀ = μ ₁ - μ ₂ . От нас требуется дать точечную оценку для Δ ₀ и построить для нее двухсторонний доверительный интервал .

СОВЕТ : Для построения Доверительного интервала нам потребуется знание следующих понятий:

• дисперсия и стандартное отклонение ,
• выборочное распределение статистики ,
• уровень доверия/ уровень значимости ,
• стандартное нормальное распределение и его квантили .

Примечание : Если заданное значение Δ ₀ равно 0, то мы предполагаем, что средние этих распределений совпадают.

Примечание : Рассматриваемая здесь задача имеет много общего с задачей о построении доверительного интервала для оценки среднего (случай, когда имеется только одно распределение). Подробнее о построении такого доверительного интервала см. в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL .

Примечание : Вышеуказанные распределения не обязательно являются нормальными . Однако, требуется чтобы выполнялись условия применимости Центральной предельной теоремы .

Примечание : Случай, когда дисперсии распределений известны, кажется несколько натянутым, т.к. обычно на практике дисперсии неизвестны, а если и известны, то, скорее всего, известно и среднее , которое определить часто гораздо легче, чем дисперсию. Поэтому, данная задача имеет скорее академический интерес, чем практический. Вычисление доверительного интервала в случае неизвестных дисперсий приведено в этой статье .

Точечной оценкой для μ ₁ - μ ₂ является разница между средними значениями, вычисленными на основании выборок из этих (независимых) распределений, т.е. Хср ₁ - Хср ₂ . Это следует из свойства математического ожидания : Е(Хср ₁ - Хср ₂ )= Е(Хср ₁ )-Е(Хср ₂ )= μ ₁ - μ ₂

Если разница Хср ₁ - Хср ₂ не попадает в границы доверительного интервала , то у нас будет основание считать, что разница между средними значениями этих распределений не равна Δ ₀ . А если Хср ₁ - Хср ₂ попадает в границы доверительного интервала , то с определенной долей вероятности можно утверждать, что μ ₁ - μ ₂ =Δ ₀ .

На основании свойств дисперсии имеем, что VAR(Хср ₁ - Хср ₂ )= VAR(Хср ₁ )+ VAR(Хср ₂ ) = σ ₁ ² /n ₁ + σ ₂ ² /n ₂

По аналогии с доверительным интервалом для среднего сразу запишем выражение для вычисления двухстороннего доверительного интервала для μ ₁ - μ ₂ :

где Z _α/2 – верхний α/2-квантиль стандартного нормального распределения (такое значение случайной величины z , что P ( z >= Z _α/2 )=α/2 ). α – уровень значимости .

Чтобы вычислить Z _α/2 для различных уровней значимости (10%; 5%; 1%) используйте формулу =НОРМ.СТ.ОБР(1- α /2) .

Задача

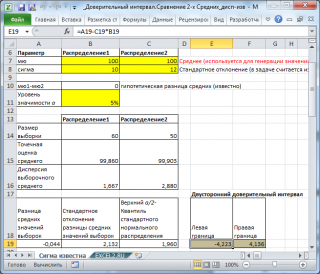
В файле примера решена задача для построения двустороннего доверительного интервала для разницы двух средних значений нормальных распределений .

Для наглядности доверительный интервал построен относительно μ ₁ - μ ₂ .

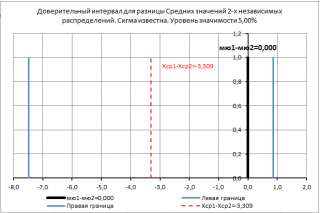
Значения выборки генерируются с помощью формулы =НОРМ.ОБР(СЛЧИС();B$7;B$8) , поэтому при перерасчете листа значения выборки обновляются.

СОВЕТ : О проверке гипотез о разнице средних значений 2-х распределений см. статью Двухвыборочный z-тест для средних в MS EXCEL . О построении других доверительных интервалов см. статью Доверительные интервалы в MS EXCEL .