Центральная предельная теорема в EXCEL
26 ноября 2016 г.
- Группы статей
- Статистический вывод
Продемонстрируем основные выводы Центральной предельной теоремы с помощью MS EXCEL : построим выборочное распределение среднего, рассчитаем стандартную ошибку и сравним значения, полученные на основе выборки, с выводами ЦПТ.
Нормальное распределение часто используется на практике для вычисления вероятностей случайной величины. Центральная предельная теорема ( ЦПТ, Central Limit Theorem ) является теоретическим обоснованием этого заключения.
Статья получилась объемная. Для облегчения навигации ниже приведено содержание статьи:
- Классическая ЦПТ
- Примеры расчета вероятности в MS EXCEL с использованием ЦПТ
- Как работает ЦПТ при n=3 и n=10
- Алгоритм решения задач с применением классической ЦПТ
- Альтернативная формулировка ЦПТ
Классическая ЦПТ
Пусть делается
выборка
размера
n
из распределения со
средним значением
μ и
стандартным отклонением
σ (распределение не обязательно является
нормальным
). По мере увеличения размера
выборки
n
,
распределение Выборочного среднего
(Х
ср
)
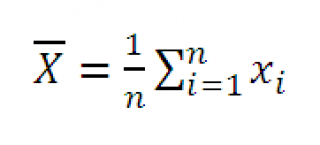
стремится к нормальному распределению со средним значением μ и стандартным отклонением равным σ/√n
Примечание : Про статистики и их выборочные распределения можно прочитать в статье Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL .
Покажем почему стандартное отклонение выборочного среднего равно σ/√n.
Каждое отдельное наблюдение X i в выборке имеет дисперсию σ 2 . Из свойств дисперсии , следует, что сумма независимых случайных величин в выборке , т.е. х 1 +х 2 …+х n , имеет дисперсию n*σ 2 , а стандартное отклонение этой суммы равно КОРЕНЬ(n) *σ . Чтобы найти стандартное отклонение среднего выборки нужно разделить стандартное отклонение суммы на n. В результате получим, что стандартное отклонение выборочного среднего равно σ/√n.
Т.к. обычно стандартное отклонение исходного распределения, из которого взята выборка, неизвестно, то в расчетах вместо σ используют ее оценку s - стандартное отклонение выборки .
Соответствующая величина s/√n, где n – размер выборки , имеет специальное название: Стандартная ошибка ( Standard Error of the Mean , SE M ) .
Примечание : Термин SEM иногда также может использоваться для стандартного отклонения выборочного распределения среднего.
Примечание : Хотя Стандартная ошибка является, по сути, стандартным отклонением , ее специальное название обусловлено стремлением подчеркнуть, что она показывает величину неопределенности выборочного среднего . Стандартная ошибка оценивает насколько выборочное среднее Х ср отличается от среднего значения μ исходного распределения. А термин стандартное отклонение обычно используют для обозначения величины изменчивости отдельных элементов выборки от среднего .
Для применения ЦПТ необходимо, чтобы были выполнены следующие условия:
- отдельные наблюдения в выборке должны быть независимыми;
- наблюдения берутся из одной и той же генеральной совокупности , т.е. имеют одинаковое распределение с параметрами μ и σ ;
- размер выборки n должен быть «достаточно большим» (см. пояснения ниже).
Примечание : Выборочное среднее является случайной величиной. Есливыполнены вышеуказанные условия, то Выборочное среднее распределено по нормальному закону . При этом не требуется, чтобы исходное распределение, из которого делается выборка , должно быть нормальным .
Примечание : Несмотря, что отдельные значения x i подчиняются какому-то неизвестному нам закону распределения, процедура объединения многих значений для вычисления суммы или среднего , приводит к нормальному распределению (для которого мы умеем вычислять вероятности). Зачастую, имеет смысл говорить, является распределение нормальным или нет, только в отношении суммы или среднего .
Примеры расчета вероятности в MS EXCEL с использованием ЦПТ
Задача1 . Предприятие производит плавленые сырки. Номинальный вес сырка должен составлять 100 грамм. По естественным причинам, вес каждого сырка отличается от номинала. Из опыта известно, что средний вес сырка составляет 105г, а стандартное отклонение равно 15г. Чтобы избежать потери репутации фирмы вес сырка не должен быть слишком мал, но он не должен быть слишком велик, т.к. при этом увеличиваются расходы. Известно, что любую упаковку из 30 штук сырков отбраковывают, если средний вес сырка в ней меньше 95г и больше чем 110г. Какая часть упаковок будет отбракована при 100% контроле?
Чтобы найти вероятность (долю отбракованных упаковок), мы должны знать распределение случайной величины - веса упаковки. Хотя мы не знаем формы распределения отдельного сырка (это распределение не обязательно нормальное ), но из ЦПТ нам известно, что вес упаковки будет распределен по нормальному закону . Осталось определить параметры этого распределения.
Примечание : Хотя в ЦПТ сказано, что по нормальному закону распределено выборочное среднее , но очевидно, что выборочное распределение суммы также будет распределено по нормальному закону , но с другими параметрами.
Из условий задачи мы знаем, что среднее значение веса упаковки сырков равно 30шт * 105г . Мы также можем вычислить стандартное отклонение этого выборочного распределения .
Стандартное отклонение известно только для сырка ( 15г ), но из свойства дисперсии для независимых случайных величин (считаем, что веса сырков получаются случайным образом) можно вычислить Стандартное отклонение для упаковки: Var(x 1 +…+x 30 )= Var(x 1 )+…+ Var(x 30 )=30* Var(x)
Т.к. считаем, что все веса х i имеют одинаковое распределение, то случайную величину (вес сырка) обозначим просто х.
Следовательно, стандартное отклонение упаковки сырков =15*КОРЕНЬ(30)
Сначала определим вероятность, того что упаковка сырков будет весить менее 95*30г. В MS EXCEL это можно сделать с помощью формулы: =НОРМ.РАСП(95*30; 105*30; 15*КОРЕНЬ(30); ИСТИНА)=0,013%
Теперь определим вероятность того, что упаковка сырков будет весить больше 110*30г. =1-НОРМ.РАСП(110*30; 105*30; 15*КОРЕНЬ(30); ИСТИНА)=3,395%
Таким образом, отбраковано будет 3,395%+0,013%=3,407% продукции.
Тот же результат можно получить при расчете через среднее значение одного сырка: =НОРМ.РАСП(95; 105; 15/КОРЕНЬ(30); ИСТИНА)+ 1-НОРМ.РАСП(110; 105; 15/КОРЕНЬ(30); ИСТИНА)
Задача2 . Из свойств нормального распределения можно ожидать, что примерно в 95% случаях выборочное среднее будет находиться в пределах 2-х стандартных ошибок от среднего генеральной совокупности (исходного распределения, из которого взята выборка ), т.е. в пределах:
-2*s/КОРЕНЬ(n)<μ<2*s/КОРЕНЬ(n)
Например, пусть размер выборки n=30, среднее генеральной совокупности μ =0, а вычисленное на основе выборки стандартное отклонение s=5.
В этом случае стандартная ошибка = 5/КОРЕНЬ(30)
Покажем с помощью формулы MS EXCEL, что искомая вероятность действительно близка к 95%: =1-((1-НОРМ.РАСП(2*5/КОРЕНЬ(30);0;5/КОРЕНЬ(30);ИСТИНА))+ НОРМ.РАСП(-2*5/КОРЕНЬ(30);0;5/КОРЕНЬ(30);ИСТИНА))=95,45%
Как работает ЦПТ при n=3 и n=10
Для демонстрации выводов ЦПТ проведем «оценку нормальности» распределения выборочного среднего при n=3 и n=10.
В качестве исходного распределения возьмем Дискретное равномерное распределение [1;6], описывающее вероятность выпадения определенной грани при бросании игральной кости.
Как известно, среднее значение этого распределения =(1+6)/2=3,5 ; а стандартное отклонение =КОРЕНЬ(((6-1+1)^2-1)/12)=1,708
С помощью MS EXCEL произведем 100 серий по 3 броска кубика (n=3) и 100 серий по 10 бросков (n=10).
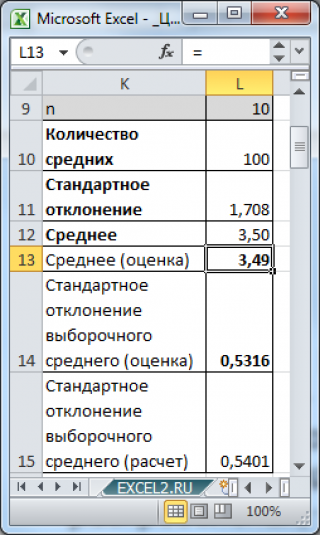
Для каждой серии бросков (т.е. для каждой выборки ) будем вычислять выборочное среднее. Затем вычислим среднее Выборочных средних и стандартную ошибку . Убедимся, что в соответствии с ЦПТ , эти значения равны 3,5 и 1,708/КОРЕНЬ(n) , соответственно.
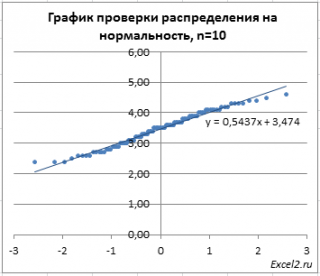
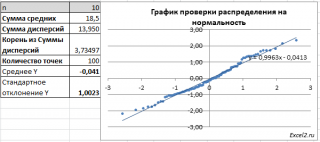
Также построим графики проверки распределения на нормальность , чтобы убедиться, что выборочное среднее распределено по нормальному закону , и частотные гистограммы для исходного равномерного распределения и распределения выборочного среднего.
Все вышеуказанные расчеты приведены в файле примера на листе ЦПТ Классик .
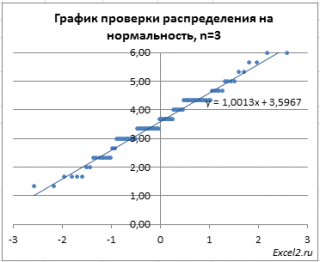
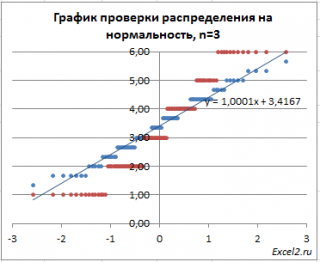
При n=3 График проверки распределения на нормальность будет соответствовать прямой очень условно (сохраняется дискретность данных, унаследованная от исходного распределения), но для n=10 – соответствие нормальному распределению будет хорошим.
Примечание : В качестве иллюстрации сравним графики проверки распределения на нормальность при n=3 и исходного равномерного дискретного распределения [1; 6], т.е. для n=1 (красные точки на рисунке ниже). Как видно на рисунке, значения, взятые из равномерного распределения, располагаются четко выраженными группами.
Среднее и Стандартная ошибка Выборочного распределения среднего близки к расчетным значениям, предсказанным ЦПТ .
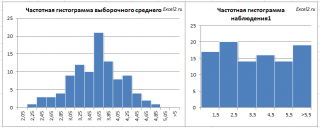
Для n=10 видно, что разброс значений выборочного среднего (гистограмма слева) не имеет ничего общего с гистограммой, полученной на основе выборки из исходного равномерного распределения (гистограмма справа).
Вывод : С помощью MS EXCEL мы продемонстрировали как работает ЦПТ : не смотря на то, что исходное распределение по форме не имеет ничего общего с нормальным , уже при небольшом n=10 выборочное среднее распределено по закону близкому к нормальному с тем же средним значением и со стандартным отклонением равным стандартной ошибке .
На практике часто требуется определить размер выборки n, достаточный, чтобы распределение выборочного среднего было достаточно близко к нормальному. Очевидно, что асимптотическое приближение распределения выборочного среднего зависит от исходного распределения, из которого берется выборка (если исходное распределение имеет сильную асимметрию , то распределение выборочного среднего будет медленнее приближаться к нормальному с ростом n). На практике исходное распределение неизвестно, поэтому обычно предполагается, что размер выборки должен быть n=>30.
]]> Алгоритм решения задач с применением классической ЦПТ
Вы проводите аудит крупного банка. Банковский служащий сообщил Вам, что средний депозит в банке составляет 200 долл., а стандартное отклонение равно 45 долл. Вам нужно убедиться в истинности информации, сообщенной менеджером, поэтому Вы решаете взять данные по случайным 50 депозитам. Дайте описание выборочного распределения среднего при n =50. Предполагая, что сообщенные менеджером характеристики распределения верны, вычислить вероятность, что рассчитанное Вами среднее значение выборки будет меньше 190 долл.
СОВЕТ : Отличное изложение материала по данной теме приведено на сайте http://brownmath.com/swt/chap08.htm ]]> (англ.)
Сначала дадим описание выборочного распределения среднего . Зачем нам это нужно? Дело в том, чтобы вычислить вероятность необходимо знать распределение вероятности. Т.е. нужно показать, что выборочное среднее распределено по нормальному закону.
Напомним, что для того, чтобы описать любое распределение необходимо вычислить его среднее , разброс и форму .
Форма распределения . Для того, чтобы решить задачу необходимо убедиться, что выборочное распределение среднего является нормальным (выполняются условия применимости ЦПТ). Как правило, для этого необходимо проверить 2 условия:
- размер выборки не должен превышать 10% от генеральной совокупности ;
- размер выборки достаточен, чтобы, несмотря на форму исходного распределения, распределение выборочного среднего было нормальным . Обычно достаточно, чтобы n было больше 30.
Будем считать, что первое условие выполнено (пусть известно, что в банке более 1000 депозитов), соответственно, 50 депозитов составляет менее 10% от общего количества депозитов банка. Исходное распределение, скорее всего, будет смещенным влево, т.к. обычно большинство депозитов небольшого и среднего размера, а крупных депозитов гораздо меньше. Размер выборки является достаточно большим (50>30), чтобы гарантировать, что форма распределения выборочного среднего является близкой к нормальному распределению .
Среднее . Среднее выборочного распределения , согласно ЦПТ , равно среднему исходного распределения, т.е. в нашем случае 200 долл.
Разброс . Стандартное отклонение выборочного среднего ( стандартная ошибка ), согласно ЦПТ, равна =45/КОРЕНЬ(50)=6,36 .
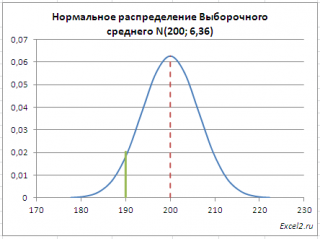
Теперь переходим непосредственно к решению задачи. Сначала построим график плотности распределения выборочного среднего N(200; 45/КОРЕНЬ(50)).
Зеленая вертикальная линия соответствует х=190 долл.
По условиям задачи мы взяли выборку из 50 депозитов и вычислили среднее этой выборки (Хср). Теперь рассчитаем вероятность того, что Хср будет меньше 190 долл. Это можно сделать с помощью формулы =НОРМ.РАСП(190; 200; 45/КОРЕНЬ(50); ИСТИНА)=0,058
Таким образом, если Х ср , вычисленное по 50 депозитам, окажется меньше 190 долл., то, это может стать серьезным основанием для сомнений в истинности слов банковского служащего (утверждавшего, что средний банковский депозит равен 200 долл.), т.к. это является маловероятным событием (<6%).
Расчеты приведены в файле примера на листе Задача .
Примечание : Частой ошибкой при решении подобных задач является неправильное использование стандартного отклонения , т.е. когда вместо стандартной ошибки используют известное стандартное отклонение исходного распределения (45 долл.), которое не обязательно является нормальным . Но, даже если исходное распределение нормальное , то вычисленное значение вероятности (в нашем случае оно будет около 40%) всегда существенно выше правильного значения (примерно 6%). Это соответствует схеме расчета, если бы мы выбрали лишь 1 депозит (вместо 50) и попытались бы на основании его значения принять решение об истинности слов служащего банка.
Резюме : Чаще всего на практике распределение, из которого делается выборка не известно (можно лишь предположить, что распределение банковских депозитов, скорее всего, скошено влево, т.к. обычно небольшие вклады составляют наибольшее количество). Но, не зная математического выражения для распределения, мы не можем оценить вероятность извлечь определенное значение из него. Именно в таких случаях нам помогает ЦПТ .
Альтернативная формулировка ЦПТ
Теперь рассмотрим как работает ЦПТ в случае, когда случайная величина является суммой случайных величин, распределенных по различным законам с различными средними и стандартными отклонениями .
Если x
1
, x
2
, x
3
, … x
n
– случайные величины с известными значениями
среднего μ
i
и
стандартного отклонения
σ
i
, и y= x
1
+x
2
+x
3
+ … +x
n
, то распределение
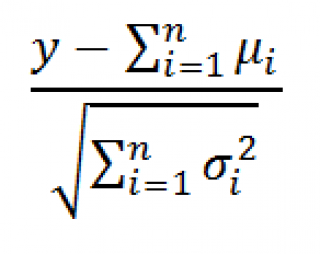
приближается к стандартному нормальному распределению N (0;1) при n стремящемуся к бесконечности.
Другими словами ЦПТ утверждает, что сумма n независимых случайных величин при достаточно большом n , будет распределена по нормальному закону со средним значением равным сумме средних значений этих случайных величин и дисперсией равной сумме их дисперсий , т.е. по закону
Как и в случае классической ЦПТ , для демонстрации выводов ЦПТ используем MS EXCEL. В качестве исходных распределений возьмем 4 биномиальных распределения B(0,1; 20), 3 дискретных равномерных распределения U[1;5] и 3 непрерывных равномерных распределения [0;1). Т.е. рассмотрим случай применения ЦПТ при n=10.
Как видно на рисунке ниже, случайная величина
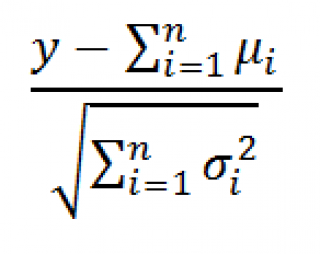 , где y= x
1
+x
2
+x
3
+ … +x
10
распределена примерно по
стандартному нормальному распределению
.
, где y= x
1
+x
2
+x
3
+ … +x
10
распределена примерно по
стандартному нормальному распределению
.
Все вышеуказанные расчеты приведены в файле примера на листе ЦПТ Альтернатива .
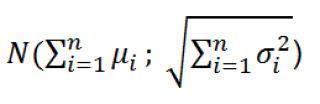
Комментарии