Бета распределение. Непрерывные распределения в EXCEL

Рассмотрим Бета-распределение, вычислим его математическое ожидание, дисперсию, моду. С помощью функции MS EXCEL БЕТА.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметров распределения.

Бета-распределение (англ. Beta - distribution ) зависит от 2-х параметров: α ( альфа)>0 (определяет форму распределения) и b ( бета)>0 (определяет масштаб).

Плотность вероятности этого распределения задается следующей формулой:

где Г(a) – гамма-функция:

если a – положительное целое, то Г(a)=(a-1)!

СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .

В отличие от многих других непрерывных распределений, диапазон изменения случайной величины, имеющей Бета-распределение , ограничен отрезком [A; B]. Вне этого отрезка плотность распределения равна 0. Границы этого отрезка задаются исследователем в зависимости от задачи. Если А=0, а B=1, то такое Бета-распределение называется стандартным.

Бета-распределение имеет обозначение Beta (альфа; бета).

Примечание : Если параметры альфа и бета = 1, то Бета распределение превращается в непрерывное равномерное распределение , т.е. Beta(1; 1; A; B) = U(A; B).

В общем случае функция распределения не может быть выражена в элементарных функциях, поэтому ее вычисляют численными методами, например, с помощью функции MS EXCEL БЕТА.РАСП() .

Математическое ожидание и дисперсия задаются следующими выражениями:

Бета-распределение часто используется для описания процессов, обладающих естественными нижним и верхним пределами. Например, Бета-распределение применяется в методе PERT (Project Evaluation and Review Technique) для оценки продолжительности работ по проекту. Бета-распределение является адекватной моделью для описания доли минералов, содержащихся в горной породе; доли солнечной радиации, поглощенной материалом и др.

Бета-распределение в MS EXCEL

В MS EXCEL, начиная с версии 2010, для Бета-распределения имеется функция БЕТА.РАСП() , английское название - BETA.DIST(), которая позволяет вычислить плотность вероятности и интегральную функцию распределения (вероятность, что случайная величина X, имеющая Бета-распределение , примет значение меньше или равное x).

Примечание : До MS EXCEL 2010 в EXCEL была функция БЕТАРАСП() , которая позволяет вычислить только интегральную функцию распределения . БЕТАРАСП() оставлена в MS EXCEL 2010 для совместимости.

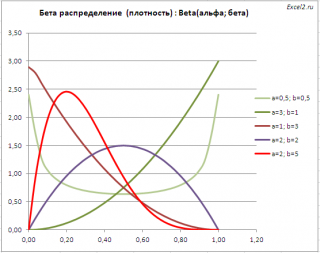
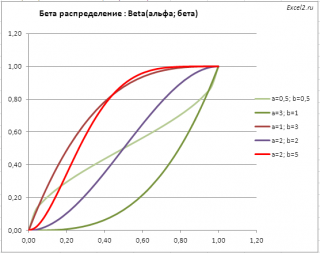
Графики функций

В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения при нескольких параметрах альфа и бета .

Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .

Примечание : Для удобства написания формул в файле примера для параметров распределения альфа и бета созданы соответствующие Имена .

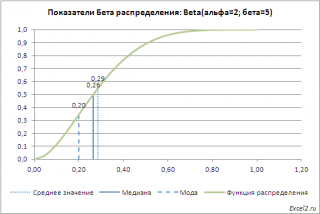
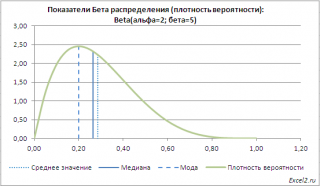
В файле примера также построены графики плотности вероятности и функции распределения с отмеченными значениями среднего , медианы и моды .

Генерация случайных чисел и оценка параметров

Используя обратную функцию распределения (или значения квантилей ( p - quantile ) , см. статью про Квантили ) можно сгенерировать значения случайной величины, имеющей Бета-распределение . Для этого нужно использовать формулу:

=БЕТА.ОБР(СЛЧИС(); альфа; бета; А; B)

СОВЕТ : Т.к. генерирование случайных чисел происходит с помощью функции СЛЧИС() , то нажимая клавишу F9 , можно каждый раз получать новую выборку и, соответственно, новую оценку параметров.

Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).

Теперь имея массив случайных чисел, сгенерированных с заданными параметрами распределения альфа и бета (пусть их будет 200), оценим параметры распределения.

Оценку параметров альфа и бета можно сделать с помощью метода моментов (предполагается, что параметры А и В известны):

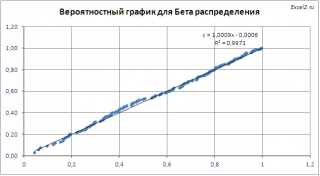
Чтобы визуально убедиться, что выборка взята из Бета-распределения , в файле примера на листе Генерация построен соответствующий Вероятностный график (probability plot) .

Т.к. форма Бета-распределения существенно зависит от его параметров, то для модификации оси Y вероятностного графика лучше использовать обратную функцию Бета-распределения с параметрами альфа и бета равными их точечным оценкам, полученным на основании выборки .

Примечание : При построении диаграммы использован тип график с маркерами . Подробнее о построении диаграмм см. Основы построения диаграмм в MS EXCEL .

Примечание : В файле примера на листе Задача приведено решение задачи об определении вероятности завершить строительство в указанный срок.

СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .